실습: LSTM으로 MNIST 분류 구현하기
이번에는 양방향 다층 LSTM을 활용하여 MNIST 분류기를 구현해보고자 합니다. 앞서 CNN 기반의 MNIST 분류기를 만들었는데요. 당시에 이미 구현된 선형 계층 기반의 분류 프로젝트 코드를 아주 약간만 수정하여 훌륭하게 동작하는 CNN 분류기를 구현할 수 있었습니다. 마찬가지로 이번에도 해당 프로젝트에 LSTM 기반 분류기를 추가하여 프로젝트를 고도화하도록 하겠습니다.
모델 구조 설계
이 문제의 입출력 데이터의 형태를 머릿속에 떠올려봅시다. 입력은 $28\times28$ 행렬입니다. 우리는 이것을 순서 데이터처럼 다룰 것이므로 28 차원의 벡터가 28개 있는 것이라고 생각하겠습니다. 그리고 출력은 클래스에 대한 확률 분포가 나와야 합니다. 거기서 가장 높은 확률 값을 갖는 클래스 레이블 인덱스를 뽑으면 예측 레이블이 됩니다. 즉 이 문제는 다대일 형태라고 볼 수 있습니다. 다대일 형태의 문제이므로 양방향 RNN을 쓸 수 있습니다. 따라서 우리는 양방향 다층 LSTM을 구성하여 MNIST 분류기를 구현하도록 하겠습니다.
다음의 그림이 이 과정을 잘 도식화 한 것인데요. 행렬로 구성된 이미지가 벡터로 구성된 순서 데이터로 취급되어 나뉘어져 RNN의 입력으로 들어가는 것을 볼 수 있습니다.
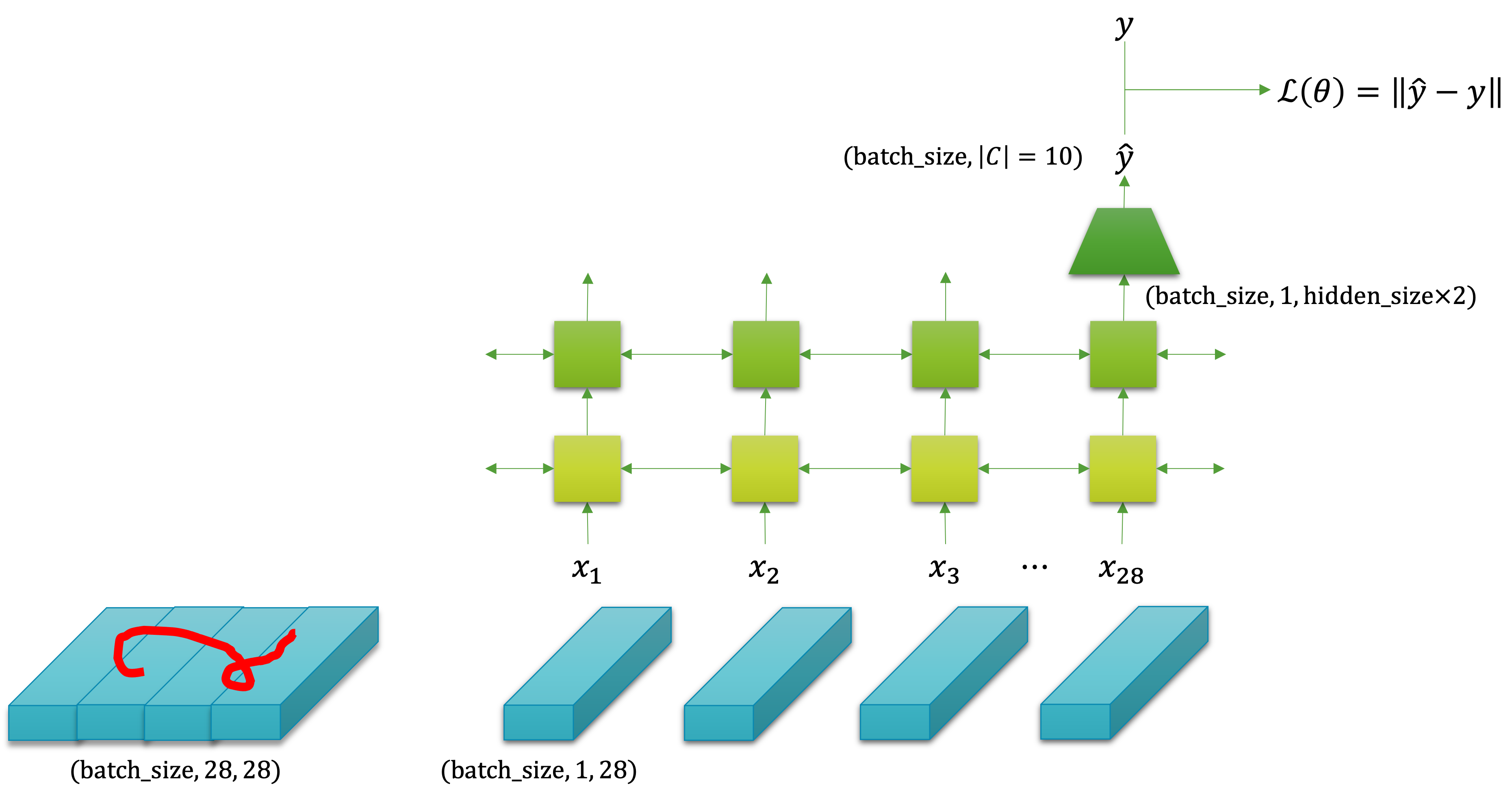
우리는 순환 신경망의 마지막 계층의 마지막 순서의 출력 텐서를 받아서 소프트맥스 함수에 넣기 위해, 선형 계층과 활성 함수 등을 활용하여 비선형 차원 축소를 수행할 것입니다. 그럼 $(N,|\mathcal{C}|)$ 크기의 텐서를 얻을 수 있고, 이것은 미니배치의 각 샘플별 클래스에 대한 확률 값을 담은 텐서가 될 것입니다. 이 텐서를 활용하여 교차 엔트로피 손실 함수에 넣으면 손실 값을 구할 수 있고, 경사하강법을 통해 가중치 파라미터를 업데이트 할 수 있을 것입니다.
모델 클래스 구현
모델 클래스는 다른 모델들과 마찬가지로 ./mnist_classifier/models/rnn.py 에 구현하도록 합니다. 다음의 코드를 살펴보면 이전 방법들에 비해 더욱 간결한 것을 확인할 수 있습니다. 앞서 다른 구조의 모델들은 서브 모듈을 클래스로 선언하고 활용하였던 반면에, 지금은 파이토치에서 제공하는 nn.LSTM 클래스를 활용해서 간단하게 분류기를 구현하기 때문입니다.
import torch
import torch.nn as nn
class SequenceClassifier(nn.Module):
def __init__(
self,
input_size,
hidden_size,
output_size,
n_layers=4,
dropout_p=.2,
):
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.n_layers = n_layers
self.dropout_p = dropout_p
super().__init__()
self.rnn = nn.LSTM(
input_size=input_size,
hidden_size=hidden_size,
num_layers=n_layers,
batch_first=True,
dropout=dropout_p,
bidirectional=True,
)
self.layers = nn.Sequential(
nn.ReLU(),
nn.BatchNorm1d(hidden_size * 2),
nn.Linear(hidden_size * 2, output_size),
nn.LogSoftmax(dim=-1),
)
def forward(self, x):
# |x| = (batch_size, h, w)
z, _ = self.rnn(x)
# |z| = (batch_size, h, hidden_size * 2)
z = z[:, -1]
# |z| = (batch_size, hidden_size * 2)
y = self.layers(z)
# |y| = (batch_size, output_size)
return y
먼저 nn.Module 을 상속받아 SequenceClassifier 클래스를 선언하였고, init 메서드와 forward 메서드를 오버라이드 하였습니다. init 메서드를 먼저 살펴보면 nn.LSTM 클래스 객체를 선언하여 self.rnn 에 할당하는 것을 볼 수 있습니다. bidirectional 인자를 통해 양방향 순환 신경망을 구현하고, num_layers 인자를 통해 다계층을 구현합니다. 그리고 dropout 인자를 통해 LSTM 내부 계층 사이사이에 드랍아웃을 넣어주도록 합니다.
그리고 가장 중요한 점은 batch_first 인자입니다. 해당 인자의 기본 값은 False 로 되어 있는데, True 를 준 것을 볼 수 있습니다. 만약 이 값을 True 로 주지 않으면 우리는 앞서 우리가 배운 입출력 텐서 모양 대신에 다음의 모양을 얻게 됩니다.
\[\begin{gathered} (N,\text{length},\text{input\_size})\Rightarrow(\text{length},N,\text{input\_size}) \\ (N,\text{length},\#\text{direction}\times\text{hidden\_size})\Rightarrow(\text{length},N,\#\text{direction}\times\text{hidden\_size}) \end{gathered}\]가장 앞에 위치하던 미니배치에 대한 차원이 두 번째가 되고, 두 번째에 위치하던 순서에 대한 차원이 가장 앞으로 오게 되는 것을 볼 수 있습니다. 파이토치가 내부적으로 병렬 연산을 수행하기 위해서 텐서의 차원을 이처럼 다루고 있기 때문인데요. 순환 신경망을 바깥에서 다루는 우리는 이러한 텐서의 모양이 심히 헷갈릴 수 있기 때문에 항상 True 에 놓고 사용하는 것을 권장합니다.
그리고 nn.Sequential 클래스에 필요한 활성 함수, 배치 정규화, 선형 계층 그리고 로그 소프트맥스log-softmax 계층을 넣어 객체를 생성한 후 self.layers 변수에 할당하는 것을 볼 수 있습니다.
이어서 forward 메서드에서는 init 메서드에서 생성된 객체들을 활용하여 연산을 수행하는데요. 가장 먼저 self.rnn 에 입력 텐서를 넣어주고 출력을 받는 것을 볼 수 있습니다. 사실 순환 신경망 객체들은 출력과 마지막 순서의 은닉 상태 두 가지 텐서를 항상 반환하는데요. (그리고 LSTM 이므로 셀 상태가 은닉 상태와 함께 튜플tuple로 반환됩니다.) 지금은 다대일 형태의 문제 접근법이므로 출력 텐서만 활용할 것이기 때문에 나머지 반환 값은 _ 로 받아버렸습니다. 이 LSTM 의 출력 텐서는 모든 입력 순서에 대해서 반환되었기 때문에, z[:, -1] 슬라이싱을 통해 마지막 순서의 값만 얻어오고, 이것을 self.layers 에 통과시켜 모델 최종 출력 텐서를 얻습니다. 그럼 모델 바깥의 Trainer 클래스에서 이 출력 텐서를 받아 손실 값을 계산하겠지요.
train.py 와 utils.py 수정하기
train.py의 define_argparser 함수에 새로운 인자들을 받기위한 준비를 합니다. 먼저 새로운 모델 타입이 구현되었기 때문에 choices 인자에 “rnn” 을 추가합니다.
p.add_argument("--model", default="fc", choices=["fc", "cnn", "rnn"])
그리고 LSTM 의 은닉 상태 크기를 정해주기 위한 hidden_size 라는 인자를 추가합니다.
p.add_argument("--hidden_size", type=int, default=128)
그리고 utils.py 의 get_model 함수에는 config.model 이 “rnn” 일 때, SequenceClassifier 를 생성하여 반환하도록 코드를 추가합니다.
def get_model(input_size, output_size, config, device):
if config.model == "fc":
model = ImageClassifier(
input_size=input_size,
output_size=output_size,
hidden_sizes=get_hidden_sizes(
input_size,
output_size,
config.n_layers
),
use_batch_norm=not config.use_dropout,
dropout_p=config.dropout_p,
).to(device)
elif config.model == "cnn":
model = ConvolutionalClassifier(output_size)
elif config.model == "rnn":
model = SequenceClassifier(
input_size=input_size,
hidden_size=config.hidden_size,
output_size=output_size,
n_layers=config.n_layers,
dropout_p=config.dropout_p,
)
else:
raise NotImplementedError
return model
이제 끝입니다. 이와 같은 적은 양의 수정 만으로도 이제 우리는 RNN 기반의 MNIST 분류기를 학습할 수 있게 되었습니다. 다음의 명령어를 통해 학습을 진행해봅시다.
$ python train.py --model_fn ./model.pth --n_epochs 20 --model rnn --n_layers 4 --hidden_size 256
Train: torch.Size([48000, 28, 28]) torch.Size([48000])
Valid: torch.Size([12000, 28, 28]) torch.Size([12000])
SequenceClassifier(
(rnn): LSTM(28, 256, num_layers=4, batch_first=True, dropout=0.3, bidirectional=True)
(layers): Sequential(
(0): ReLU()
(1): BatchNorm1d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): Linear(in_features=512, out_features=10, bias=True)
(3): LogSoftmax(dim=-1)
)
)
Adam (
Parameter Group 0
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
lr: 0.001
weight_decay: 0
)
NLLLoss()
Epoch(1/20): train_loss=4.4981e-01 valid_loss=1.6719e-01 lowest_loss=1.6719e-01
Epoch(2/20): train_loss=1.2586e-01 valid_loss=1.2428e-01 lowest_loss=1.2428e-01
Epoch(3/20): train_loss=8.7505e-02 valid_loss=8.6867e-02 lowest_loss=8.6867e-02
Epoch(4/20): train_loss=6.4460e-02 valid_loss=7.6098e-02 lowest_loss=7.6098e-02
Epoch(5/20): train_loss=4.8930e-02 valid_loss=7.9153e-02 lowest_loss=7.6098e-02
Epoch(6/20): train_loss=4.3516e-02 valid_loss=6.9273e-02 lowest_loss=6.9273e-02
Epoch(7/20): train_loss=3.9331e-02 valid_loss=6.1692e-02 lowest_loss=6.1692e-02
Epoch(8/20): train_loss=3.6852e-02 valid_loss=6.0280e-02 lowest_loss=6.0280e-02
Epoch(9/20): train_loss=3.0019e-02 valid_loss=4.4652e-02 lowest_loss=4.4652e-02
Epoch(10/20): train_loss=2.2890e-02 valid_loss=5.5313e-02 lowest_loss=4.4652e-02
Epoch(11/20): train_loss=2.5589e-02 valid_loss=5.0306e-02 lowest_loss=4.4652e-02
Epoch(12/20): train_loss=2.4667e-02 valid_loss=4.3369e-02 lowest_loss=4.3369e-02
Epoch(13/20): train_loss=1.9621e-02 valid_loss=5.1580e-02 lowest_loss=4.3369e-02
Epoch(14/20): train_loss=2.0608e-02 valid_loss=5.2379e-02 lowest_loss=4.3369e-02
Epoch(15/20): train_loss=1.9362e-02 valid_loss=4.6227e-02 lowest_loss=4.3369e-02
Epoch(16/20): train_loss=1.4802e-02 valid_loss=4.4920e-02 lowest_loss=4.3369e-02
Epoch(17/20): train_loss=1.3107e-02 valid_loss=5.1847e-02 lowest_loss=4.3369e-02
Epoch(18/20): train_loss=1.7017e-02 valid_loss=6.7198e-02 lowest_loss=4.3369e-02
Epoch(19/20): train_loss=1.5467e-02 valid_loss=4.6087e-02 lowest_loss=4.3369e-02
Epoch(20/20): train_loss=1.0572e-02 valid_loss=4.8228e-02 lowest_loss=4.3369e-02
predict.ipynb 실행하기
이 파일은 수정할 필요도 없습니다. 바로 실행해봅니다.
... torch.Size([10000, 28, 28]) torch.Size([10000])
Accuracy: 0.9884
앞서 구현하였던 CNN 기반의 모델에 필적하는 테스트 성능이 나오는 것을 확인할 수 있습니다. 그리고 또 재미있게도 20개의 테스트 샘플에 대해서 CNN 기반의 모델과 같이 다른 샘플이긴 하지만 1개를 틀리는 것을 볼 수 있습니다.
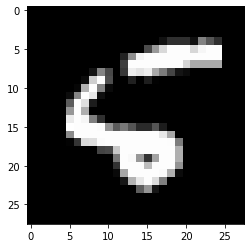
원래 정답 레이블이 5인 이 테스트 샘플에 대해서 6이라고 예측하였는데요. (물론 다시 모델을 학습하면 아마 다르게 동작할 것입니다.) 사람이 보기에도 약간 6의 형태를 띄고 있으므로 정신승리를 하며 넘어가도록 하겠습니다.
마무리하며
필자가 학습한 모델 기반으로 테스트셋에 대해서 성능을 구하였을 때, 다음과 같은 결과를 얻을 수 있었습니다.
| 모델 | 검증 손실 | 테스트 정확도(acc.) |
|---|---|---|
| FC 기반 | 6.7707e-02 | 98.37% |
| CNN 기반 | 2.9458e-02 | 99.16% |
| RNN 기반 | 4.3369e-02 | 98.84% |
일단은 CNN 기반의 분류기가 가장 좋은 성능을 보여주는 것을 볼 수 있는데요. 사실 지금은 단 한번의 실험을 수행한 것이므로 정확하게 알 수는 없습니다. 여기서 만약 좀 더 정확한 성능비교를 하고 싶다면, 검증셋을 기반으로 하이퍼 파라미터 튜닝을 수행하고, 각 모델별로 최소 5번 이상의 학습 및 평가를 수행하여 테스트 성능의 평균 및 표준편차를 비교하면 됩니다. 또한 사실 각 모델들의 가중치 파라미터 갯수가 다르므로 공정한 비교라고 볼 수 없습니다. 만약 정말 어떤 알고리즘이 가장 좋은지 궁금하다면 파라미터 갯수를 최대한 동일하게 맞춘 후에 실험을 진행해야 할 것입니다.
아마 지금까지의 과정을 살펴보았다면 여러분들이 실제 머신러닝 프로젝트를 수행할 때 어떤 방식으로 코드를 구현하고 실험을 진행해야 할지 약간의 힌트를 얻을 수 있었을 것입니다. 보다시피 주피터 노트북이 아닌 CLIcommand-line interface 환경에서 코드의 수정 없이 하이퍼 파라미터 튜닝을 수행할 수 있으며, 적은 양의 코드 수정만으로 새로운 모델 구조나 알고리즘 수정을 수행할 수 있습니다. 또한 이처럼 학습 및 추론 템플릿을 잘 구성해 놓으면 다른 프로젝트에도 쉽게 재사용 가능하므로, 독자분들도 여러분만의 학습 및 실험 환경을 구축해보길 권장합니다.