Brief Introduction to Calculus
이번 시간에는 경사 하강법을 배우기에 앞서 필요한 미분에 대해서 간단히 이야기 하도록 하겠습니다. 비록 고등학교 시절처럼 손으로 직접 미분을 계산할 필요는 전혀 없지만, 미분과 관련된 개념은 매우 중요합니다. 따라서 좀 더 자세히 공부하고 싶으신 분들은 유튜브를 검색해보시면 고등학교나 각종 시험을 위한 유명 1타 강사들이 올려놓은 영상들이 많으므로 참고 바랍니다.
기울기
미분을 이야기하기에 앞서 기울기란 무엇인지 이야기해보죠. 기울기란 $x$ 증가량에 대한 $y$ 증가량으로 정의됩니다. 즉, $x$ 가 변화한 양에 비해 $y$ 가 변화한 양이 클수록 기울기는 커지게 됩니다. 이것을 그림으로 나타내면 다음과 같습니다. 주어진 삼각형의 밑변에 대해서 삼각형의 높이가 높아질수록 빗면의 기울기가 커지게 될 것입니다.

이것을 수식으로 나타내면 다음과 같습니다. 2차원 좌표 상에서 두 점 $(x_1, y_1), (x_2, y_2)$ 가 주어졌을 때, 두 점 사이의 기울기를 구하는 공식입니다.
\[\begin{gathered} \frac{\Delta{y}}{\Delta{x}}=\frac{y_2-y_1}{x_2-x_1} \end{gathered}\]그럼 다음 그림과 같이 두 점을 이은 직선의 기울기를 구할 수 있을겁니다.
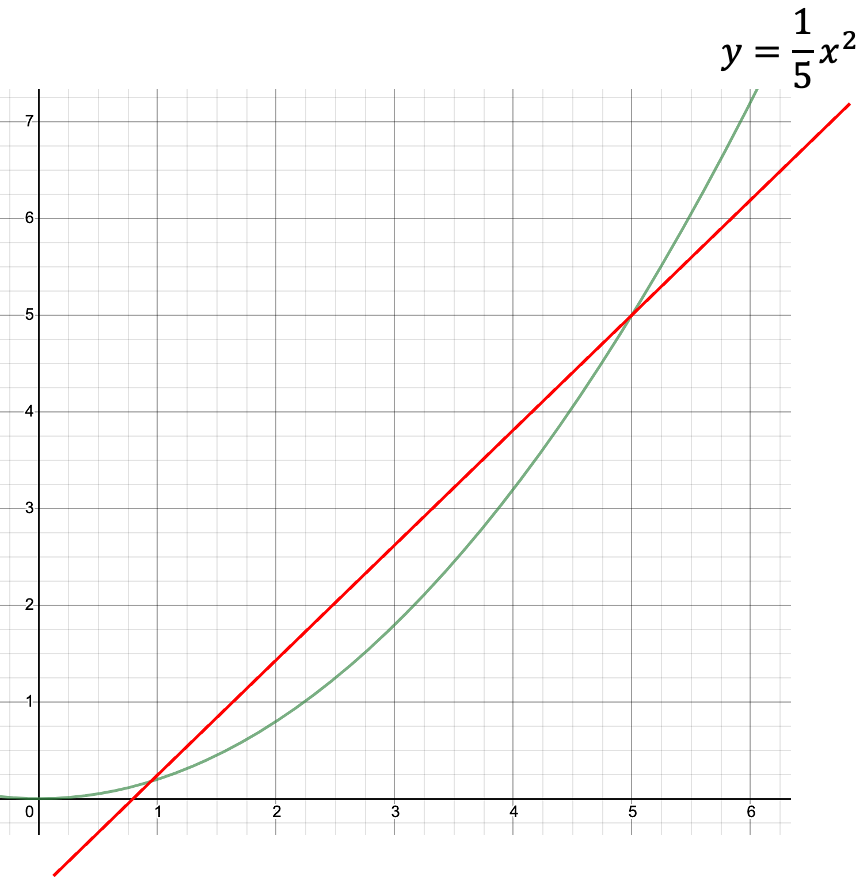
앞서 그림에서는 $f(x)=\frac{1}{5}x^2$ 일때, $x=1$ 인 지점과 $x=5$ 인 지점 사이를 잇는 직선이 그려져 있습니다. 이 직선의 기울기는 다음과 같습니다. $x$ 의 증가량은 4이며, 우리는 이것을 $h$ 라고 표현하겠습니다.
\[\begin{gathered} \frac{\Delta{y}}{\Delta{x}}=\frac{f(1+h)-f(1)}{(1+h)-1}=\frac{f(5)-f(1)}{5-1}=\frac{5-0.2}{5-1}=\frac{4.8}{4}=1.2, \\ \text{where }h=4. \end{gathered}\]그러므로 이 직선을 표현하면 다음과 같겠군요.
\[\begin{gathered} y=1.2x-1 \end{gathered}\]극한(무한소)과 미분
이때, $x$ 의 변화량을 매우 작게 만들어 볼 수 있을 겁니다.
즉, $h=x_2-x_1$ 이라고 할 때, $h$ 를 $0$ 에 가깝게 만들어 봅니다.
\[\begin{gathered} y=f(x) \\ \frac{dy}{dx}=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{(x+h)-x} \end{gathered}\]그때 $y$ 의 변화량을 구한다면, 마찬가지로 기울기를 구할 수 있을 겁니다. 앞서는 두 점 사이의 기울기였지만, 지금은 함수 $f$ 위의 지점 $\big(x,f(x)\big)$ 에서의 접선의 기울기라고 볼 수 있을겁니다. 이때 기울기를 표현하기 위해서, 앞서 델타delta $\Delta$ 로 표현되었던 것을 $d$로 표현하였습니다. 다음 그림은 함수 $f$ 에서 $x=3$ 일때의 접선을 나타낸 것입니다.
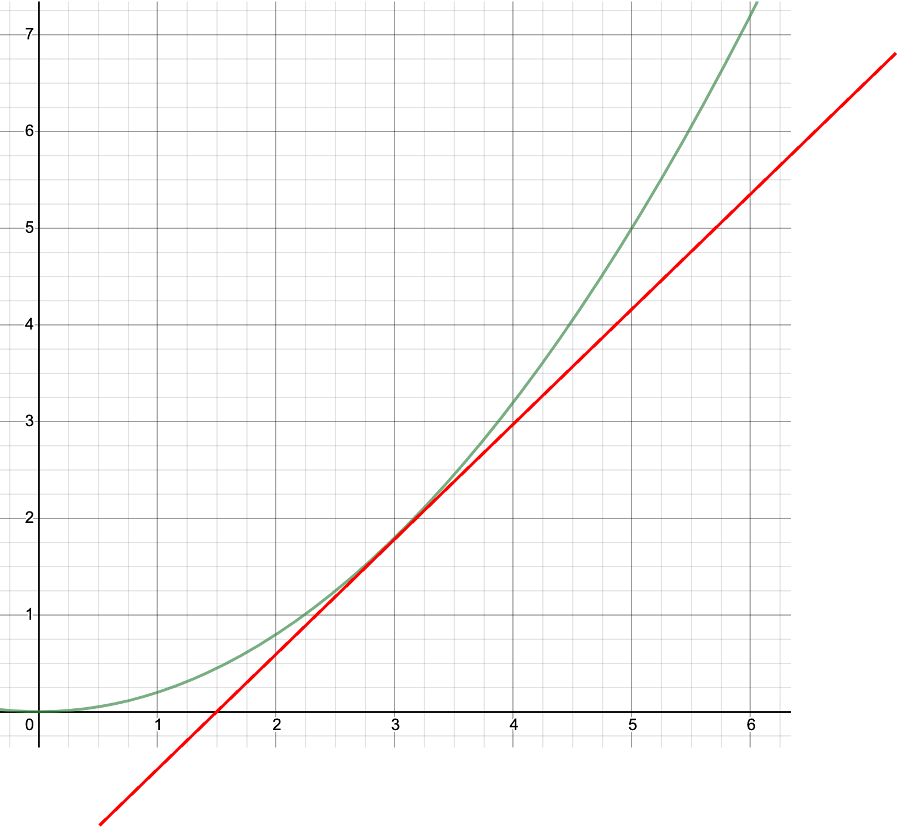
그럼 이 접선의 기울기는 어떻게 계산할까요?
도함수
앞서 그림에서처럼 함수 $f$ 가 주어져 있을 때, 특정 지점 $x$ 에 대한 접선의 기울기를 함수로 나타내 볼 수 있을 것입니다. 즉, 입력은 특정 지점 $x$ 가 될 것이고, 출력은 해당 지점에서의 함수 $f$ 의 기울기가 되겠지요. 이것을 우리는 다음과 같이 함수꼴로 표현해볼 수 있습니다.
\[\begin{gathered} g(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{(x+h)-x} \\ \\ y'=f'(x)=g(x) \end{gathered}\]이때 함수 $f$ 의 기울기를 함수로 나타낸 $g$ 를 도함수라고 부르며, 이것은 함수 $f$ 를 미분하여 얻을 수 있습니다. 함수 $f$ 를 미분한 것을 $f’$ 라고 표기하기도 합니다.
뉴턴 vs 라이프니츠
우리가 고등학교에서 배운 미분 표기법은 작은 따옴표를 붙이는 방식입니다. 이것은 동시대에 발견된 미분 방법 중에서 뉴턴의 것을 따르는 것입니다.
\[\begin{gathered} y'=f'(x) \end{gathered}\]다른 표기 방법은 독일의 라이프니츠가 만든 방식으로, 다음과 같이 분수와 비슷한 꼴로 표기됩니다.
\[\begin{gathered} \frac{dy}{dx}=\frac{df}{dx} \end{gathered}\]처음에 기울기를 이야기할 때 소개했던 형태 $\frac{\Delta{y}}{\Delta{x}}$ 와 비슷한 표현이라고 보면 될 것 같습니다. 다만 $\Delta{x}$ 가 0에 근접했을 때의 표현식이 됩니다.
합성함수 미분
우리는 비록 뉴턴 방식으로 표현하도록 학창시절에 배웠지만, 라이프니츠 방식으로 표현하면 좀 더 편리해지는 부분이 있습니다. 예를 들어 다음과 같이 합성함수가 정의되어 있다고 해보겠습니다.
\[\begin{aligned} y&=f\circ{g}(x) \\ &=f(g(x)) \\ \\ y&=f(h) \\ h&=g(x) \end{aligned}\]변수 $y$ 는 $x$ 에 의해 정해지지만, 두 함수 $f$ 와 $g$ 를 통과해야 합니다. 또는 중간 변수 $h$ 를 두어, 표현해볼 수도 있을 것입니다.
뉴턴
우리는 학창시절에 합성함수의 미분을 외우도록 강요(?) 받았습니다. 물론 그 과정에서 이 수식에 대한 유도 과정은 배웠을 수 있지만, 결국 외울 수 밖에 없었을 겁니다.
\[\begin{aligned} y'&=f'(h)\cdot{g'(x)} \\ &=f'(g(x))\cdot{g'(x)} \end{aligned}\]만약 $f(h)=h^2$ 이고, $g(x)=x^2+x$ 라면 어떻게 될까요? 먼저 두 합성함수를 전개하면 다음과 같이 될 겁니다.
\[\begin{aligned} y&=f\circ{g}(x) \\ &=(x^2+x)^2 \\ &=\big(x\cdot(x+1)\big)^2 \\ &=x^2\cdot(x^2+2x+1) \\ &=x^4+2x^3+x^2 \end{aligned}\]이것을 미분하면 다음과 같을 것입니다.[2]
\[\begin{gathered} y'=4x^3+6x^2+2x \end{gathered}\]이것이 위에서 외운 합성함수의 미분법에 따른 결과와 같은지 확인해보죠.
\[\begin{aligned} y'&=f'(h)\cdot{g'(x)} \\ &=2h\cdot(2x+1) \\ &=2(x^2+x)(2x+1) \\ &=2(2x^3+2x^2+x^2+x) \\ &=4x^3+6x^2+2x \end{aligned}\]라이프니츠
하지만 라이프니츠 방식을 쓰게 되면 좀 더 쉽게 풀 수 있습니다. 우선 앞서 언급한 라이프니츠 방식의 미분 표현법은 마치 분수처럼 취급될 수 있습니다.[1] 따라서 분모와 분자에 $dh$ 를 추가해주어 다음과 같이 표현해볼 수 있습니다.
\[\begin{gathered} \frac{dy}{dx}&=\frac{df}{dh}\cdot\frac{dh}{dx} \end{gathered}\]이것은 $y$ 를 $x$ 로 미분하는 과정은 $f$ 를 $h$ 로 미분하고, 여기에 $h$ 를 $x$ 로 미분한 것을 곱한것과 같다는 이야기가 됩니다. 실제 그런 것인지 다음 수식에서 각 변수를 함수들로 치환해보면 미분 방식과 같은 결과가 나오는 것을 볼 수 있습니다.
\[\begin{aligned} \frac{dy}{dx}&=\frac{df}{dh}\cdot\frac{dh}{dx} \\ &=f'(h)\cdot{\Big(\frac{d}{dx}g(x)\Big)} \\ &=f'(g(x))\cdot{g'(x)} \end{aligned}\]즉, 여러개의 변수가 주어진 상황에서는 라이프니츠 방식의 미분 표기법이 훨씬 직관적으로 다가오는 것을 알 수 있습니다.
[1]: 실제 분수처럼 동작하는 것은 아닙니다.
[2]: 여러분이 딥러닝을 연구/개발 할 때, 실제 미분을 손으로 계산할 필요는 없기 때문에 미분을 전혀 배우신 적이 없으시다면 이 과정은 이해 못하셔도 크게 문제되지 않습니다.