기본 확률 통계
우리는 보통 다음과 같은 표현들을 자주 볼 수 있습니다.
\[\begin{gathered} P(\text{x}=x) \\ P(\text{y}=y) \end{gathered}\]이 표현은 쉽게 말해서 변수 $\text{x}$ 가 $x$ 값을 가질 확률과 변수 $\text{y}$ 가 $y$ 값을 가질 확률을 의미한다고 볼 수 있습니다. 이때 변수들은 연속continuous 값을 갖는 변수일 수도 있고, 이산discrete 값을 갖는 변수일 수도 있습니다. 가장 중요한 차이점은 이산 확률 변수가 특정 값을 가질 확률은 구할 수 있지만, 연속 확률 변수가 특정 값을 가질 확률은 0이라는 것 입니다.
이산 확률 변수가 특정 값을 가질 확률을 나타내는 것을 확률 질량probability mass라고 부릅니다. 반대로 연속 확률 변수의 경우에는 특정 값에 대한 확률을 나타내는 것을 확률 밀도probability density를 통해서 나타낼 수 있습니다. 다시 한번 이야기하면 확률 밀도는 확률 값을 나타내는 것이 아니며, 확률 밀도를 구간에 대해서 적분하면 우리가 흔히 말하는 확률 값이 됩니다.
이것은 다음의 예를 들어 생각해볼 수 있습니다. 주사위의 경우에는 특정 면이 바닥에 닿을 확률이 1/6이 되지만, 완벽한 구의 경우에는 특정 지점이 바닥에 닿을 확률은 0이라고 볼 수 있을 것입니다. 점의 넓이는 0이기 때문입니다. 하지만 구의 특정 범위 중에 일부가 바닥에 닿을 확률은, 구의 전체 넓이 중에 특정 범위 넓이의 비율이 될 것입니다.
즉, 이산 확률 변수의 경우에는 다음과 같이 합을 통해 확률을 구할 수 있지만,
\[\begin{gathered} \sum_{x}{P(\text{x}=x)}=1\text{, where }0\le{P(\text{x}=x)}\le1\text{, }\forall{x}\in\mathcal{X}. \end{gathered}\]연속 확률 변수의 경우에는 다음과 같이 적분을 통해 구간에 대한 확률을 구할 수 있습니다.
\[\begin{gathered} \int{p(x)}\text{ }dx=1\text{, where }p(x)\ge0\text{, }\forall{x}\in\mathbb{R} \end{gathered}\]결합 확률
우리는 변수가 2개 이상인 확률 분포에 대해서도 수식으로 표현해 볼 수 있습니다.
\[\begin{gathered} P(\text{x},\text{y})=P(\text{x}=x,\text{y}=y) \end{gathered}\]이와 같이 두 개 이상의 변수를 사용하는 확률 표현을 결합 확률joint probability이라고 합니다.
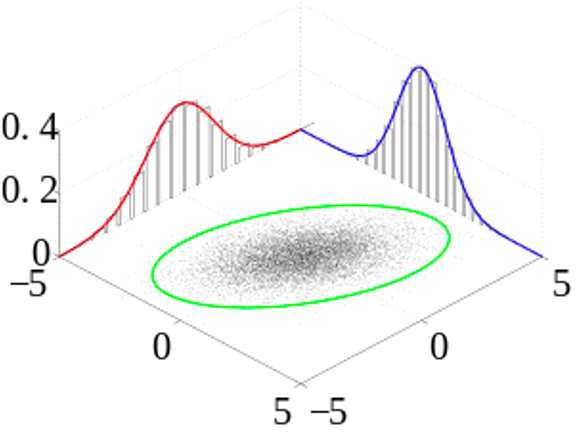
만약 두 변수가 독립이라면 각 변수의 확률의 곱으로도 나타낼 수 있습니다. 머신러닝이나 딥러닝 문제에서는 입력과 출력 등을 확률 변수로 나타낼 수 있는데요. 그럼 보통 입력 샘플을 나타내는 변수를 $\text{x}$ 로 두고, 출력 샘플을 나타내는 변수를 $\text{y}$ 로 사용하여, 결합 확률로 나타내는 경우가 많습니다.
조건부 확률
머신러닝에서 결합 확률보다 더 흔히 사용되는 것이 조건부 확률conditional probability입니다. 앞서 이야기 한 대로 입력 샘플을 $\text{x}$, 출력 샘플을 $\text{y}$ 로 표현하는 경우가 많은데요. 입력 샘플 $x$ 가 주어졌을 때, 출력 샘플 $y$ 가 나타날 확률을 $P(\text{y}=y|\text{x}=x)$ 라고 표현합니다. 이때 조건부 확률과 결합 확률과의 관계는 다음과 같습니다.
\[\begin{aligned} P(\text{y}|\text{x})&=\frac{P(\text{x},\text{y})}{P(\text{x})} \\ P(\text{x}, \text{y})&=P(\text{y}|\text{x})P(\text{x}) \end{aligned}\]이러한 조건부 확률과 결합 확률의 관계를 활용한 것이 베이즈 정리Bayes Theorem입니다. 다음의 수식에서 볼 수 있듯이, 베이즈 정리를 활용하면 조건부 확률의 앞과 뒤에 나타나는 변수의 위치를 반대로 바꿀 수 있습니다. 이 베이즈 정리 또한 머신러닝에서 굉장히 중요한 역할을 수행합니다.
\[\begin{gathered} P(h|D)=\frac{P(D|h)P(h)}{P(D)} \end{gathered}\]변수? 값? 분포? 함수?
앞서 수식들을 자세히 살펴보면 $P()$ 안에 사용되는 글씨체가 다른 것을 볼 수 있습니다. 예를 들어 확률 변수를 나타낼 때에는 $\text{x}$ 로 나타내고, 해당 변수가 어떤 값을 가지는 경우에는 그 값을 $x$ 로 나타냅니다.
\[\begin{gathered} P(\text{x}=x)=P(x) \end{gathered}\]그러므로 우리가 $P(\text{y}|x)$ 라고 표현할 경우, 이것은 변수 $\text{x}$ 에 값 $x$ 를 넣어 조건으로 주어졌을 때, 확률 분포를 의미합니다. 또는 $P(\cdot|x)$ 라고 줄여서 표현하기도 합니다. 주의할 점은 $y$ 가 아닌 $\text{y}$ 라고 표기하였기 때문에, 확률 값이 아닌 확률 분포를 의미하는 것입니다. 만약 확률 값을 나타내고자 한다면, 예전처럼 $P(y|x)$ 라고 표기하였을 것입니다.
그럼 한 발 더 나아가서 다음의 수식과 같이 함수의 형태로도 생각해볼 수 있습니다.
\[\begin{gathered} f(x)=P(\text{y}=y|\text{x}=x) \end{gathered}\]이 형태는 변수 $\text{x}$ 에 어떤 값을 주어졌을 때, 변수 $\text{y}$ 가 $y$ 값을 가질 확률 값을 나타냅니다. 만약 조건 변수의 값이 바뀐다면 확률 값도 바뀔 것입니다. 따라서 우리는 이것을 확률의 형태로 바꿔 생각하면, 조건부 변수를 함수의 입력으로 생각하고 확률 값을 함수의 출력으로 생각할 수 있습니다.
여기서 또 한 발 더 나아가면, $P(\text{y}|\text{x})$ 와 같은 형태의 함수꼴도 생각할 수 있습니다. 이 경우에는 입력의 형태는 같지만, 출력의 형태가 확률 값이 아닌 확률 분포라는 점이 바뀌게 될 것입니다. 함수의 출력이 확률 분포라는 것은, 마치 파이썬으로 치면 함수가 실수형float 값을 반환하는 것이 아닌, 분포라는 객체를 반환하는 것이라고 생각해볼 수도 있을 것 같습니다.
주변 분포
우리는 결합 확률 분포가 있을 때, 하나의 변수를 적분해서 없앨 수도 있습니다. 이것을 주변 분포marginal distribution이라고 합니다.
\[\begin{aligned} P(x)&=\int{P(x,z)}\text{ }dz \\ &=\int{P(x|z)P(z)}\text{ }dz \\ &=\int{P(z|x)P(x)}\text{ }dz=P(x)\int{P(z|x)}\text{ }dz \end{aligned}\]샘플링과 기대값
흔히 확률의 개념을 설명할 때, 주사위나 동전 던지기를 이야기 하곤 합니다. 동전 던지기를 예로 들면, 동전을 던져서 어떤 면이 나오는지 확인하는 행위는 해당 동전을 던지는 것에 대한 확률 분포에서 하나의 샘플을 추출하는 것과 같습니다. 만약 정상적인 동전이라면 던지는 행위가 반복될 수록 앞 면과 뒷 면의 비율이 같아질 것입니다.
여기서 한 발 더 나아가서, 점수 제도를 도입해보도록 하겠습니다. 동전을 던져서 앞 면이 나오면 +100 점, 뒷 면이 나오면 -100 점을 누적하도록 합니다. 그럼 동전을 반복해서 던지게 되면 내가 얻을 것으로 점수의 기대값은 얼마일까요? 우리는 초등학교 때 기대값은 확률 곱하기 값이라고 배웠습니다. 따라서 정상적인 동전이라면 앞 면이 나올 확률 50%, 뒷 면이 나올 50%를 각 점수에 곱하면 점수의 기대값을 다음과 같이 구할 수 있습니다.
\[\begin{gathered} 0.5\times100+0.5\times-100=0 \end{gathered}\]이것을 좀 더 이쁘게 써 볼 수 있습니다. 동전의 앞 면을 1, 뒷 면을 0이라고 할 때, 함수 $f$ 를 먼저 다음과 같이 정의 합니다.
\[\begin{gathered} f(x)=\begin{cases} +100 &\text{if } 1 \\ -100 &\text{if } 0 \end{cases} \end{gathered}\]그럼 동전을 던지는 행위에 대한 확률 분포를 $P(\text{x})$ 라고 할 때, 동전을 던져 얻게될 점수에 대한 기대값을 다음과 같이 표현 가능합니다. 수식을 잘 살펴보면 기대값이라는 것은 함수에 대한 확률의 가중평균weighted average임을 알 수 있습니다.
\[\begin{gathered} \mathbb{E}_{\text{x}\sim{P(\text{x})}}\big[f(\text{x})\big]=\sum_{x\in\mathcal{X}}{P(x)\cdot{f(x)}}, \\ \text{where }\mathcal{X}=\{0,1\}. \end{gathered}\]동전 던지기나 주사위 던지기의 경우에는 이산 확률 변수 및 이산 확률 분포이기 때문에 $\sum$ 을 통해서 합을 구했지만, 연속 변수의 경우에는 적분을 통해 같은 작업을 수행할 수 있습니다.