선형 계층

우리는 데이터를 모아서 알수 없는 함수 $f^*$ 를 근사하고 싶습니다. 어떤 모델로 그 함수를 근사할 수 있을까요? 이 장에서는 가장 기본 모델이 될 수 있는 선형 계층^{linear layer}에 대해서 다뤄보겠습니다. 이 선형 계층은 후에 다룰 심층신경망^{deep neural networks}의 가장 기본 구성요소가 됩니다. 뿐만 아니라, 방금 언급한 것처럼 하나의 모델로 동작할 수도 있습니다.

다음의 그림은 선형 계층을 도식화하여 나타낸 것입니다.

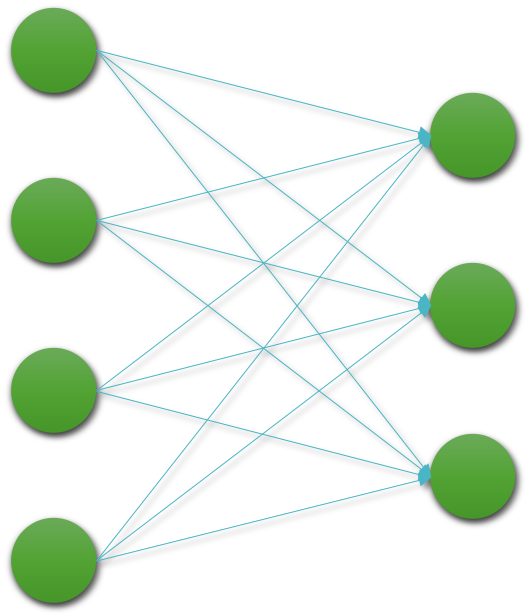
이 선형 계층 또한 하나의 함수로 볼 수 있습니다. 따라서 4개의 입력을 받아 3개의 출력을 반환하는 함수로 생각할 수 있습니다.

\[\begin{gathered} f:\mathbb{R}^4\rightarrow\mathbb{R}^3 \end{gathered}\]

즉, 앞의 수식과 같이 4차원의 실수 벡터를 입력을 받아 3차원의 실수 벡터를 반환하는 함수로 생각할 수 있습니다.

선형 계층 함수의 동작 방식

이때 이 함수가 어떻게 동작할지 정의가 되어야 합니다. 이를 위해서 함수는 가중치 파라미터^{weight paramter}를 가지고 있으며, 이 가중치 파라미터에 의해서 함수의 동작이 정의됩니다. 이 가중치 파라미터는 다음 그림과 같이 동작하게 됩니다. 각각의 출력 노드의 값은, 입력 노드로부터 들어오는 값에 가중치 파라미터 $W_{i\rightarrow{j}}$ 를 곱하고, 또 다른 가중치 파라미터 $b_j$ 를 더해주어 결정됩니다.

이 그림에서 $W$ 에는 총 $4\times3=12$ 가지의 가중치 파라미터가 존재하며 이는 다음과 같이 수식으로 표현 가능합니다.

\[\begin{gathered} W\in\mathbb{R}^{4\times3}\text{ or }|W|=(4,3). \end{gathered}\]

또한 $b$ 에는 총 $3$ 가지의 가중치 파라미터가 존재하며 이는 다음과 같이 수식으로 표현 가능합니다.

\[\begin{gathered} b\in\mathbb{R}^{3}\text{ or }|b|=(3,). \end{gathered}\]

즉, 이 동작 방식은 행렬 곱셈과 벡터의 덧셈으로 나타낼 수 있기 때문에, 이를 일반화 하여 수식으로 나타내면 다음과 표현할 수 있습니다.

\[\begin{gathered} y=f(x)=W^\top\cdot{x}+b, \\ \text{where }x\in\mathbb{R}^n\text{, }W^\top\in\mathbb{R}^{m\times{n}}\text{, }b\in\mathbb{R}^m\text{ and }y\in\mathbb{R}^m. \end{gathered}\]

입력 벡터 $x$ 는 n차원의 실수 벡터이며, 출력 벡터 $y$ 는 m차원의 실수 벡터입니다. 따라서 n차원을 m차원으로 변환해주기 위해선, $W$ 는 $n\times{m}$ 차원의 행렬이 되어야 합니다. 다시말하면, $f$ 는 다음과 같은 함수라고 볼 수 있습니다.

\[\begin{gathered} f:\mathbb{R}^n\rightarrow\mathbb{R}^m \end{gathered}\]

만약 수 백만개의 입력 벡터가 주어졌을 때, 이것을 단순히 순차적으로 처리한다면 매우 비효율적일 것입니다. 따라서 우리는 이 연산을 다수의 입력을 처리하기 위한 병렬^parallel 연산으로 생각해 볼 수도 있습니다. 우리는 N개의 n차원 벡터를 모아서 $N\times{n}$ 크기의 행렬로 만들 수 있습니다. 이것을 우리는 미니배치^mini-batch라고 부르도록 하겠습니다. 이 미니배치 행렬을 선형 계층 함수에서 처리하기 위한 수식은 다음과 같이 표현될 것입니다.

\[\begin{gathered} y=f(x)=x\cdot{W}+b, \\ \text{where }x\in\mathbb{R}^{N\times{n}}\text{, }W\in\mathbb{R}^{n\times{m}}\text{, }b\in\mathbb{R}^m\text{ and }y\in\mathbb{R}^{N\times{m}}. \end{gathered}\]

앞서 수식에서 볼 수 있듯이, 우리는 입력을 N개 모아서 미니배치 행렬로 넣어주었기 때문에, 출력도 N개의 m차원의 벡터가 모여서 $N\times{m}$ 크기의 행렬이 됩니다. 이처럼 우리는 병렬 연산을 통해 연산 속도를 높일 수 있으며, 이것은 GPU 상에서의 행렬 곱셈으로 처리됩니다. 여기서 주의할 점은 종종 표현 방식에 따라 $W$ 를 $n\times{m}$ 이 아니라 $m\times{n}$ 으로 표기하기도 합니다. 이 경우에도 전치^transpose 연산의 표기를 통해 결국 같은 연산을 수행하도록 될 것입니다.

선형 계층의 의미

선형 계층은 행렬 곱셈과 벡터의 덧셈으로 이루어져있기 때문에 선형 변환이라고 볼 수 있습니다. 따라서 선형 계층을 통해 모델을 구성할 경우, 우리는 선형 데이터에 대한 관계를 분석하거나 선형 함수를 근사할 수 있습니다.