Partial Derivative
앞서는 입력 변수가 $x$ 만 있을 때, 미분하는 방법에 대해 이야기 하였습니다. 이번에는 다음 그림과 같이 다변수가 입력으로 주어질 때 함수를 미분하는 방법에 대해 이야기하고자 합니다.
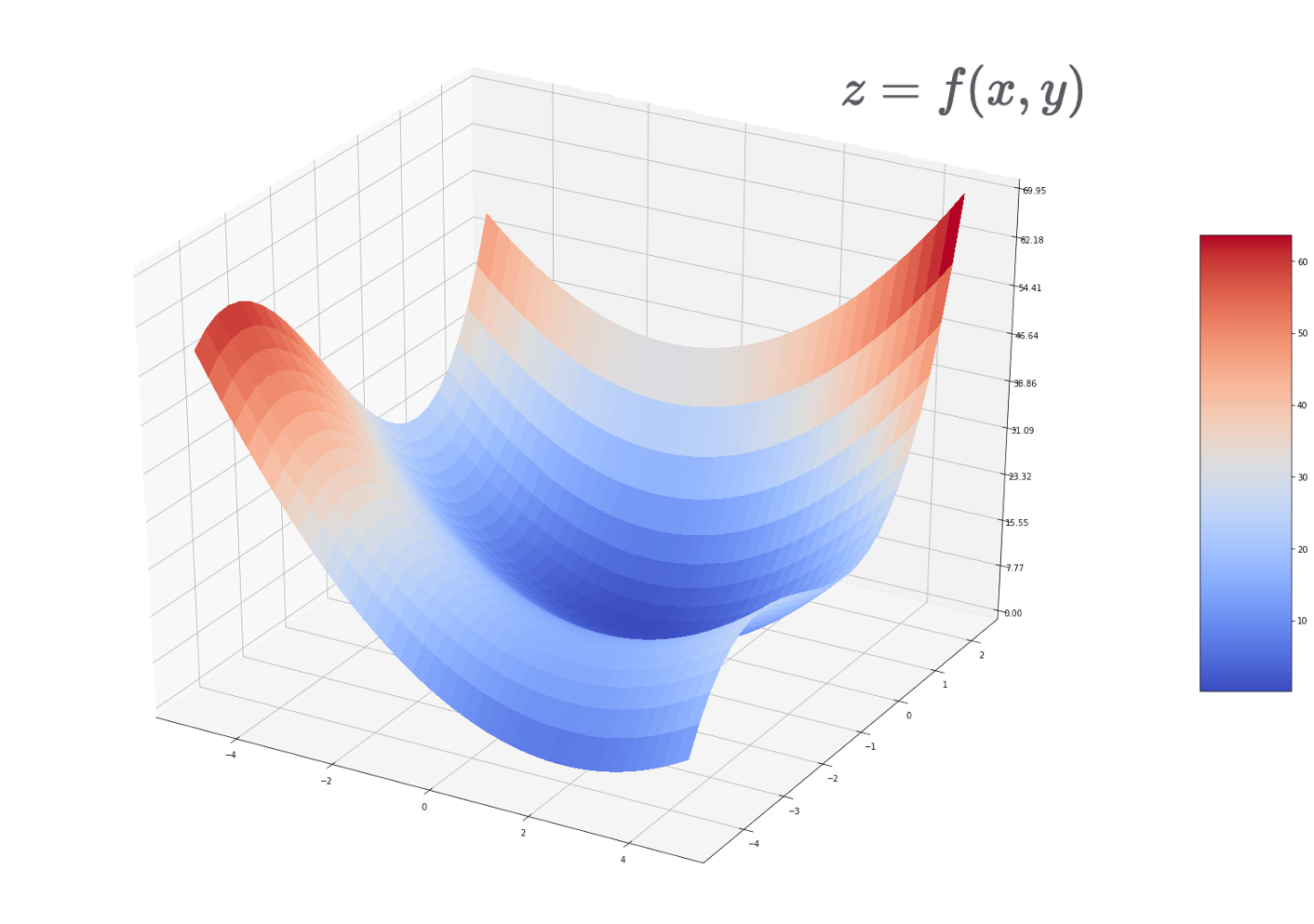
편미분
단변수 함수를 미분할 때는 1차원 상에서의 함수가 되므로, 접선의 기울기를 구하는 문제가 되었습니다. 그럼 다변수 함수를 미분할 때는 어떻게 될까요? 다음과 같이 입력변수 $x$ 와 $y$ 로 정의되는 함수가 있다고 보겠습니다.
\[\begin{gathered} z=f(x,y) \end{gathered}\]이때 우리는 하나의 입력 변수에 대해서만 미분을 수행할 수 있습니다. 이것을 우리는 편미분이라고 합니다. 즉, 다음 수식과 같이 $x$ 의 변화량을 0에 수렴하게 만들어서, 함수 $f$ 를 $x$ 로 미분할 수 있을 것입니다.
\[\begin{gathered} \frac{\partial{f}}{\partial{x}}=\lim_{h\rightarrow0}\frac{f(x+h,y)-f(x,y)}{(x+h)-x} \end{gathered}\]이때, 앞서 미분 표기와 다르게 $d$ 대신에 편미분을 뜻하는 $\partial$ 로 바뀌었습니다. 즉, 좌변이 의미하는 것은 다변수 함수 $f$ 를 입력 변수 중 하나인 $x$ 로 편미분한다는 것입니다. 다음 그림은 실제 2차원 함수의 수식을 $x$ 로 편미분 한 것을 나타냅니다.

그럼 마찬가지로 $y$ 로도 편미분 해볼 수 있겠지요.
\[\begin{gathered} \frac{\partial{f}}{\partial{y}}=\lim_{h\rightarrow0}\frac{f(x,y+h)-f(x,y)}{(y+h)-y} \end{gathered}\]각 미분 결과는 기울기의 크기를 나타냅니다. 그럼 이 다변수 함수 $f$ 에서 특정 지점 $(x,y)$ 에서의 기울기는 어떻게 될까요? 이때는 각 변수별 미분 결과를 합쳐서 벡터로 나타내게 됩니다. 즉, 1차원 함수에서의 미분 결과는 기울기의 크기인 스칼라 값이지만, 다변수 함수에서의 미분 결과는 입력 변수 갯수만큼의 차원을 갖는 벡터가 되는 것입니다.
\[\begin{gathered} \Big(\frac{\partial{f}}{\partial{x}},\frac{\partial{f}}{\partial{y}}\Big) \end{gathered}\]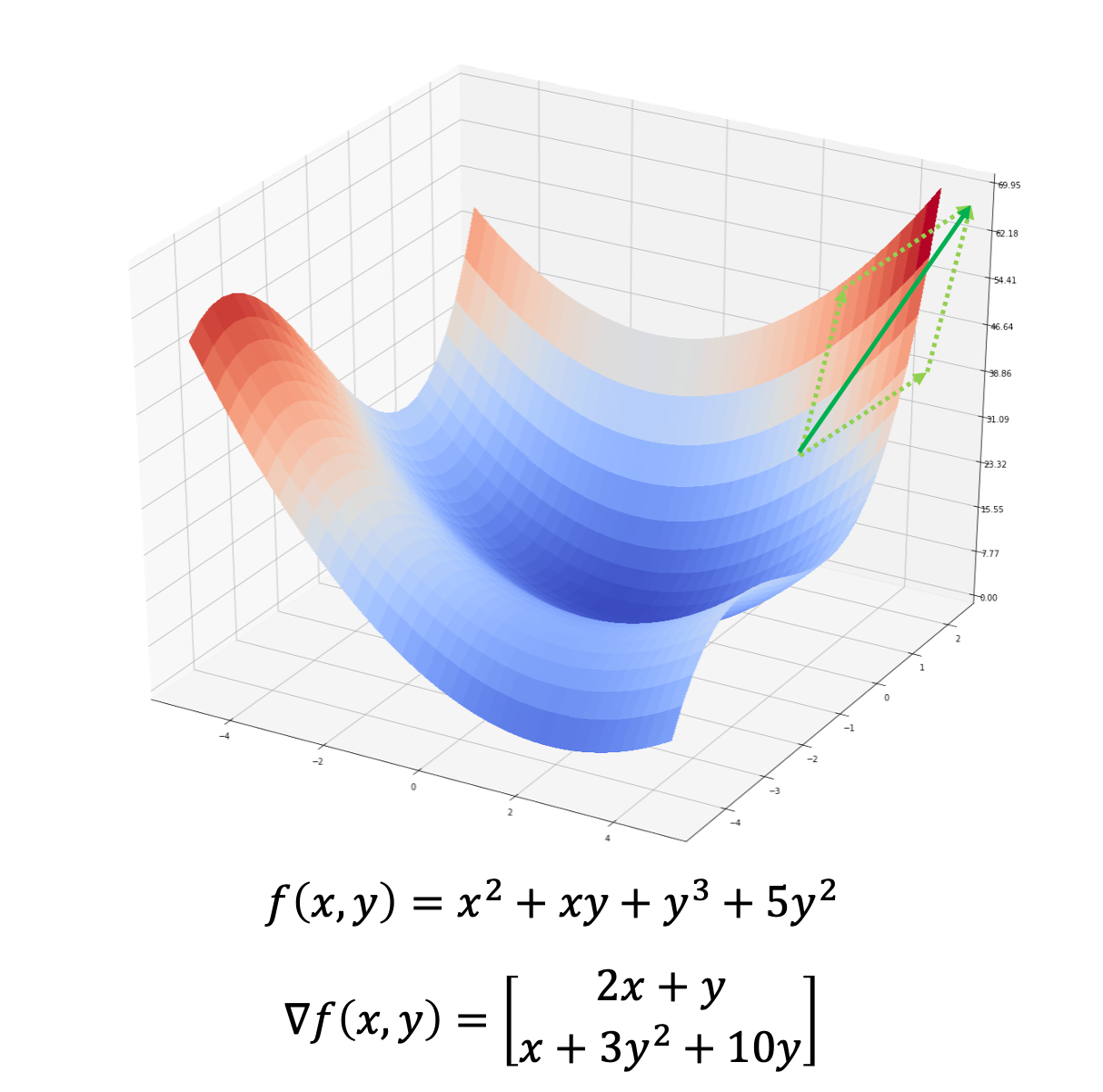
우리는 이 기울기 벡터를 그래디언트gradient라고 부릅니다. 이것은 다차원 함수로 정의된 평면에서의 접면tangent plane의 벡터라고 볼 수 있습니다.
함수의 입출력 형태
앞서 이야기한 내용을 좀 더 일반화하기에 앞서 다양한 형태의 입출력을 갖는 함수들을 살펴보도록 하겠습니다.
벡터를 입력으로 받는 함수
앞서 보았던 다변수 함수는 벡터를 입력으로 받는 것이라고 생각할 수 있습니다. 따라서 다음의 수식처럼 $n$ 차원의 벡터 $x$ 를 입력으로 받는 함수라고 볼 수 있을 겁니다.
\[\begin{gathered} y=f(\begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix})=f(x), \\ \text{where }x\in\mathbb{R}^n. \end{gathered}\]행렬을 입력으로 받는 함수
그럼 좀 더 생각을 확장하면 행렬을 입력으로 받는 함수도 생각해볼 수 있습니다.
\[\begin{gathered} y=f(\begin{bmatrix} x_{1,1} & \cdots & x_{1,m} \\ \vdots & \ddots & \vdots \\ x_{n,1} & \cdots & x_{n,m} \end{bmatrix})=f(X), \\ \text{where }X\in\mathbb{R}^{n\times{m}}. \end{gathered}\]출력이 벡터 또는 행렬인 함수
이번에는 출력이 벡터이거나 함수인 함수 형태도 생각해볼 수 있을 겁니다. 다음 수식은 각각 출력이 $n$ 차원의 벡터이거나, $n\times{m}$ 차원의 행렬인 경우를 나타냅니다.
\[\begin{gathered} y=\begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix}=f(x), \\ \text{where }y\in\mathbb{R}^n. \end{gathered}\] \[\begin{gathered} Y=\begin{bmatrix} y_{1,1} & \cdots & y_{1,m} \\ \vdots & \ddots & \vdots \\ y_{n,1} & \cdots & y_{n,m} \end{bmatrix}=f(x), \\ \text{where }Y\in\mathbb{R}^{n\times{m}}. \end{gathered}\]입력과 출력이 벡터인 함수
그럼 위를 조합하면 입력과 출력이 벡터이거나 행렬인 함수도 생각해볼 수 있을 것입니다. 다음 수식은 입력과 출력이 각각 $n$ 차원과 $m$ 차원인 함수를 수식으로 표현한 것입니다. $n$ 개의 입력을 받아 $m$ 개의 출력을 내보내는 선형 계층linear layer도 여기에 속합니다.
\[\begin{gathered} y=\begin{bmatrix} y_1 \\ \vdots \\ y_m \end{bmatrix}=f(x)=f(\begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix}), \\ \text{where }f:\mathbb{R}^n\rightarrow\mathbb{R}^m. \end{gathered}\]행렬의 미분
앞서 정리한 것을 바탕으로 편미분을 확장하여 여러 케이스에 적용해보도록 하겠습니다.
스칼라를 벡터로 미분
먼저 앞서 처음 편미분을 소개했을 때와 같이, 스칼라 형태의 출력을 갖는 다변수 입력을 받는 함수를 벡터(다변수)로 (편)미분 하는 경우를 생각해보죠. 이 경우에는 다음의 수식과 같이 나타낼 수 있습니다.
\[\begin{gathered} \frac{\partial{f}}{\partial{x}}=\nabla_{x}f=\begin{bmatrix} \frac{\partial{f}}{\partial{x_1}} \\ \vdots \\ \frac{\partial{f}}{\partial{x_n}} \end{bmatrix}, \\ \text{where }x\in\mathbb{R}^n. \end{gathered}\]먼저 함수 $f$ 의 많은 입력 중에서 일부 입력들을 미분하려는 것일 수 있으므로 편미분에 해당되어 $\frac{\partial{f}}{\partial{x}}$ 로 나타내어집니다. 그리고 벡터 $x$ 로 미분하는 것이기 때문에, 역삼각형에 기호 $x$ 를 붙여서 $\nabla_{x}f$ 로 나타낼 수도 있습니다. 그리고 이 미분 작업의 결과물은 마찬가지로 $n$ 차원의 벡터가 됩니다.
스칼라를 행렬로 미분
함수를 벡터로 미분하였던 것처럼, 스칼라 출력을 갖는 함수를 행렬로 미분할 수도 있습니다. 이 경우에는 다음과 같이 결과물도 같은 차원의 형태를 갖는 행렬로 나타납니다.
\[\begin{gathered} \frac{\partial{f}}{\partial{X}}=\nabla_X{f}=\begin{bmatrix} \frac{\partial{f}}{\partial{x_{1,1}}} & \cdots & \frac{\partial{f}}{\partial{x_{1,m}}} \\ \vdots & \ddots & \vdots \\ \frac{\partial{f}}{\partial{x_{n,1}}} & \cdots & \frac{\partial{f}}{\partial{x_{n,m}}} \end{bmatrix}, \\ \text{where }X\in\mathbb{R}^{n\times{m}} \end{gathered}\]벡터를 스칼라로 미분
단변수 $x$ 를 입력받아 벡터 형태의 출력을 갖는 함수도 생각해볼 수 있을 것입니다. 사실 이 경우에는 단변수 $x$ 를 입력받아 스칼라 출력을 갖는 함수 $f_1(x) \cdots f_n(x)$ 가 여러개 합쳐져 있는 상태라고 볼 수도 있습니다. 그러므로 다음 수식과 같이 각 함수를 미분한 것과 같을 것입니다.
\[\begin{gathered} \frac{\partial{f}}{\partial{x}}=\begin{bmatrix} \frac{\partial{f_1}}{\partial{x}} & \cdots & \frac{\partial{f_n}}{\partial{x}} \end{bmatrix}, \\ \text{where }f(x)\in\mathbb{R}^n. \end{gathered}\]만약 함수의 입력이 단변수 $x$ 만 존재한다면 다음과 같이 편미분이 아닌 미분 기호로 나타내질수도 있을 것입니다.
\[\begin{gathered} \frac{d{f}}{d{x}}=\begin{bmatrix} \frac{d{f_1}}{d{x}} & \cdots & \frac{d{f_n}}{d{x}} \end{bmatrix}, \text{where }f(x)\in\mathbb{R}^n. \end{gathered}\]벡터를 벡터로 미분
마지막으로 $m$ 차원의 벡터를 출력으로 갖는 함수 $f$ 를 $n$ 차원의 벡터 $x$ 로 미분하는 경우도 생각해볼 수 있을 것입니다. 마치 선형 계층linear layer을 미분하는 것과 같은 상황이라고 볼 수 있겠네요. 이 경우에도 함수는 다변수를 입력 받는 $m$ 개 함수들이 합쳐져 있는 것으로 볼 수 있을 것입니다. 따라서 함수를 벡터 $x$ 의 요소들 $x_1\cdots{x_n}$ 로 편미분 할 경우에는 벡터 형태로 미분 결과물이 나올 것이고, 각 $m$ 개의 함수들을 벡터 $x$ 로 편미분 하는 경우에는 벡터를 전치행렬transpose로 바꾼 형태로 미분 결과물이 나올 것입니다. 마지막으로 각 $m$ 개의 함수들을 벡터 $x$ 의 각 $n$ 개의 요소들로 미분할 경우, $n\times{m}$ 의 행렬 형태로 미분 결과물이 나올 것입니다.
\[\begin{gathered} \begin{aligned} \frac{\partial{f}}{\partial{x}}&=\begin{bmatrix} \frac{\partial{f}}{\partial{x_1}} \\ \vdots \\ \frac{\partial{f}}{\partial{x_n}} \end{bmatrix}=\begin{bmatrix} \frac{\partial{f_1}}{\partial{x}} & \cdots & \frac{\partial{f_m}}{\partial{x}} \end{bmatrix} \\ &=\begin{bmatrix} \frac{\partial{f_1}}{\partial{x_1}} & \cdots & \frac{\partial{f_m}}{\partial{x_1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial{f_1}}{\partial{x_n}} & \cdots & \frac{\partial{f_m}}{\partial{x_n}} \end{bmatrix} \end{aligned}, \\ \text{where }x\in\mathbb{R}^n\text{ and }f(x)\in\mathbb{R}^m. \end{gathered}\]마찬가지로 위의 미분을 손으로 계산할 필요는 전혀 없습니다. 하지만 앞으로 배울 경사하강법의 원활한 이해를 위해서는 입력과 출력의 형태에 대한 이해는 필요합니다.