심층신경망

이제까지 우리는 선형 계층^{linear layer}하나를 활용하여 회귀^regression와 분류^{classification}문제를 풀어왔습니다. 돌아보면 그때 풀고자 했던 문제들은 모두 선형 데이터와 관련된 문제들이었습니다.

하지만 알고보면 다음 그림과 같이 비선형^non-linear 함수 형태를 근사해야 할 수도 있습니다. 예를 들어 이 그림은 감기에 걸렸을 때 날짜 경과에 따른 증상 발현의 정도를 나타낸 것이라고 생각해보겠습니다. 앞서 선형 데이터의 예제와 같이 아웃라이어^outlier들이 존재하긴 하지만 대부분의 샘플들은 노란색 선 근처에 존재하는 것을 볼 수 있습니다. 이 노란색 선을 우리가 근사하고자 하는 함수 $f^*$ 라고 할 때, 기존의 선형 회귀 모델과 로지스틱 회귀 모델로는 이런 비선형 문제를 해결할 수 없습니다.

사실 세상은 선형 데이터들로만 구성되어 있지 않습니다. 오히려 알고보면 비선형 데이터들이 더 많을 것 같은데요. 예를들어 이미지, 텍스트, 음성과 같은 데이터들은 비선형 데이터일 뿐만 아니라, 높은 차원의 공간^{high-dimensional space}에 분포하고 있는 데이터이므로 심지어 앞선 그림과 같이 눈으로 데이터의 분포를 확인하는 것조차 불가능합니다.

기존의 머신러닝^{machine learning} 기법들은 이런 비선형적이고 높은 차원의 데이터들을 다루기에는 어려움이 많았습니다. 하지만 딥러닝^{deep learning}의 시대에 들어오면서, 심층신경망^{deep neural networks}은 이러한 문제들을 해결하는데 뛰어남을 보여주었습니다. 이제 우리도 심층신경망을 통해 문제를 해결하는 방법을 살펴보고자 합니다.

심층신경망이란?

아마 이 책을 읽는 독자분들 중에서는 심층신경망에 대해 처음 듣는 분들은 없을 것이라 생각합니다. 따라서 심층신경망이란 계층^layer을 깊게 쌓아올린 것이라는 말도 많이 들어보셨을 것입니다. 심층신경망은 서로 다른 선형 계층^{linear layer}을 깊게 쌓아 구성할 수 있습니다. 그런데 그냥 단순히 선형 계층을 많이 쌓는 것만으로 충분할까요?

\[\begin{gathered} h=x\cdot{W_1}+b_1 \\ y=h\cdot{W_2}+b_2 \end{gathered}\]

예를 들어, 앞의 수식과 같이 두 개의 선형 계층을 가진 모델을 생각해볼 수 있습니다. 이 모델은 그럼 두 개의 계층을 지닌 심층신경망이 되는 것일까요? 아쉽게도 아닙니다. 그 이유는 다음 수식과 같이 $h$ 를 앞 계층의 수식으로 치환하여 전개해보면 알 수 있습니다.

\[\begin{aligned} y&=h\cdot{W_2}+b_2 \\ &=(x\cdot{W_1}+b_1)\cdot{W_2}+b_2 \\ &=x\cdot\underbrace{ {W_1}\cdot{W_2} }_{ \text{linear} }+b_1^\intercal\cdot{W_2}+b_2 \\ &=x\cdot{W'}+b' \end{aligned}\]

재미있게도 전개해보면 두 선형 계층을 통과하는 것은 또 다른 하나의 선형 계층을 통과하는 것과 같음을 알 수 있습니다. 즉, 선형 계층을 아무리 깊게 쌓아봤자 여전히 우리는 하나의 선형 계층을 마주하게되는 것입니다. 이런 방법으로는 비선형 문제를 풀 수 없다는 의미입니다. 어떻게 해야 할까요?

우리는 앞서 시그모이드^sigmoid와 탄에이치^TanH와 같은 활성 함수^{activation function}들에 대해 배웠습니다. 다음 그림은 시그모이드를 나타낸 것인데요.

그림에서 볼 수 있듯이 이 함수는 전 구간에서 미분 가능한 비선형적인 단조 증가 형태를 띄고 있습니다. 가장 간단한 방법은 선형 계층을 쌓을 때 그 사이에 이와 같은 비선형 함수를 끼워 넣는 것입니다.^[1] 그럼 다음 그림과 같이 심층 신경망이 구성 될 수 있습니다.

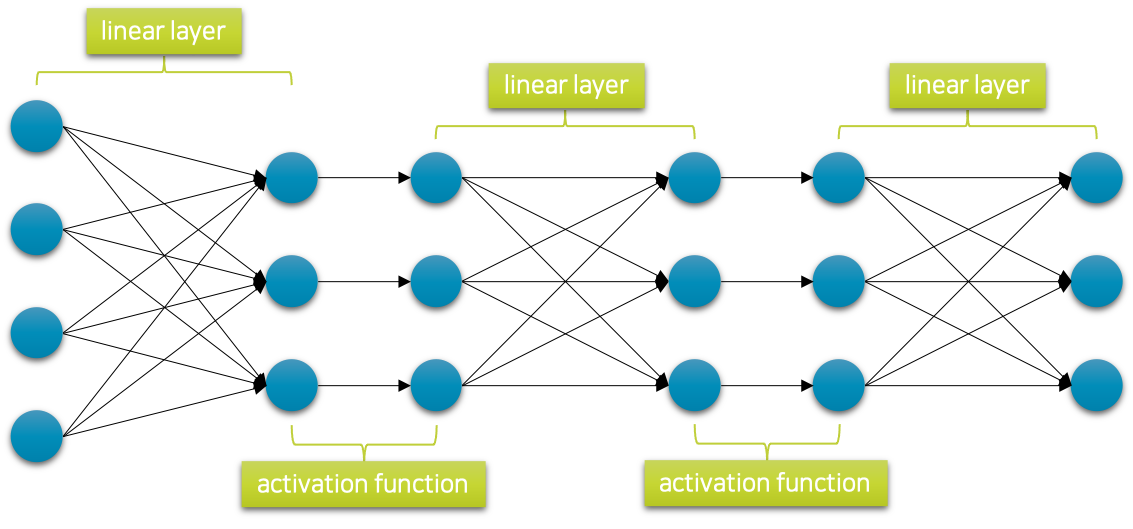
이렇게 심층신경망을 구성할 수 있게 되고, 이제 이러한 심층신경망을 통해 복잡한 비선형 데이터에 대한 관계를 학습하거나 문제를 해결할 수 있게 되었습니다.

[1]: 꼭 시그모이드나 탄에이치일 필요는 없습니다. 미분 가능한 (되도록이면 단조증가 형태의) 비선형 함수이면 됩니다.

심층신경망의 크기

이론적으로 심층신경망은 세상에 존재하는 그 어떤 형태의 함수도 근사할 수 있음이 증명되어 있습니다.^[2] 따라서 신경망의 깊이와 너비를 조절하여 함수가 더 복잡한 형태의 데이터 관계나 문제를 해결할 수 있도록 할 수 있습니다. 보통은 다음 그림과 같이 신경망을 구성할 때, 계층이 진행될수록 너비가 줄어드는 형태로 설계를 하게 되는데요. 이때 너비가 줄어드는 양을 조절하거나, 계층을 더 깊게 쌓을수록 네트워크의 표현 능력은 일반적으로 더 향상되게 됩니다. 신경망을 더 넓고 깊게 쌓아, 더 복잡하고 어려운 데이터의 관계를 배우거나 문제를 풀 수 있습니다.

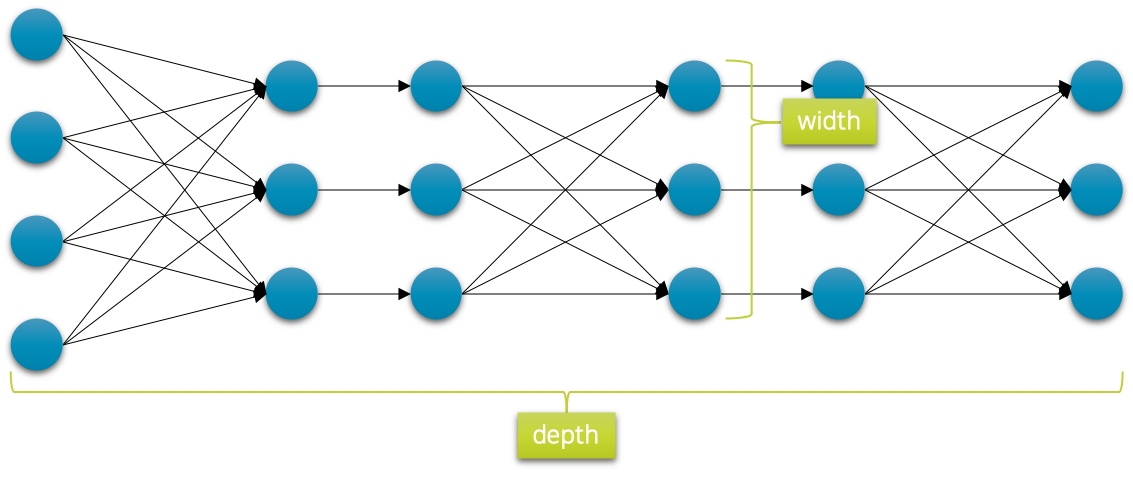
하지만 깊이가 깊어지거나 너비가 넓어지게 되면 계층들의 가중치 파라미터 크기가 늘어나게 되면서, 경사하강법^{gradient descent}을 통해 최적화해야 하는 공간의 차원 크기도 같이 늘어나게 됩니다. 따라서 비록 신경망의 크기가 커지더라도 최적화에 어려움을 겪을 수 있어, 실제로는 성능이 향상되는데에는 한계를 겪을 수 있습니다. 오히려 더 작은 신경망으로도 충분히 해결되는 경우에는 독으로 작용할 수도 있습니다. 따라서 적절한 신경망의 크기를 정해주어 신경망이 데이터의 관계를 배우는데 잘 최적화가 진행될 수 있도록 도와주는 것이 중요합니다.

[2]: Universal Approximation Theorem, UAT - https://en.wikipedia.org/wiki/Universal_approximation_theorem

---