맥스 풀링과 스트라이드 기법
보통 심층신경망에서는 고차원 공간의 데이터를 저차원 공간으로 비선형적으로 풀어내 표현하는 과정에서 샘플의 특징을 추출하고 학습을 한다고 볼 수 있습니다. 하지만 예를 들어 우리가 즐겨쓰는 형태의 합성곱 계층인 $3\times3\text{ kernel }+1\text{ padding}$ 형태에서는 입력과 출력의 크기가 같습니다. 또한 패딩이 없거나 커널의 크기가 커져서 출력의 크기가 입력의 크기에 비해 작아지더라도, 입력에서의 상대적인 위치가 출력에서도 보존되기 때문에 차원 축소 과정을 거친다고 보기 어려울 수 있습니다. 이때 우리는 맥스 풀링 또는 스트라이드 기법을 활용하여 다운 샘플링과 같은 차원 축소를 수행할 수 있습니다.
맥스 풀링
다음의 그림은 맥스 풀링max-pooling 함수의 동작 방식을 그림을 나타낸 것입니다.
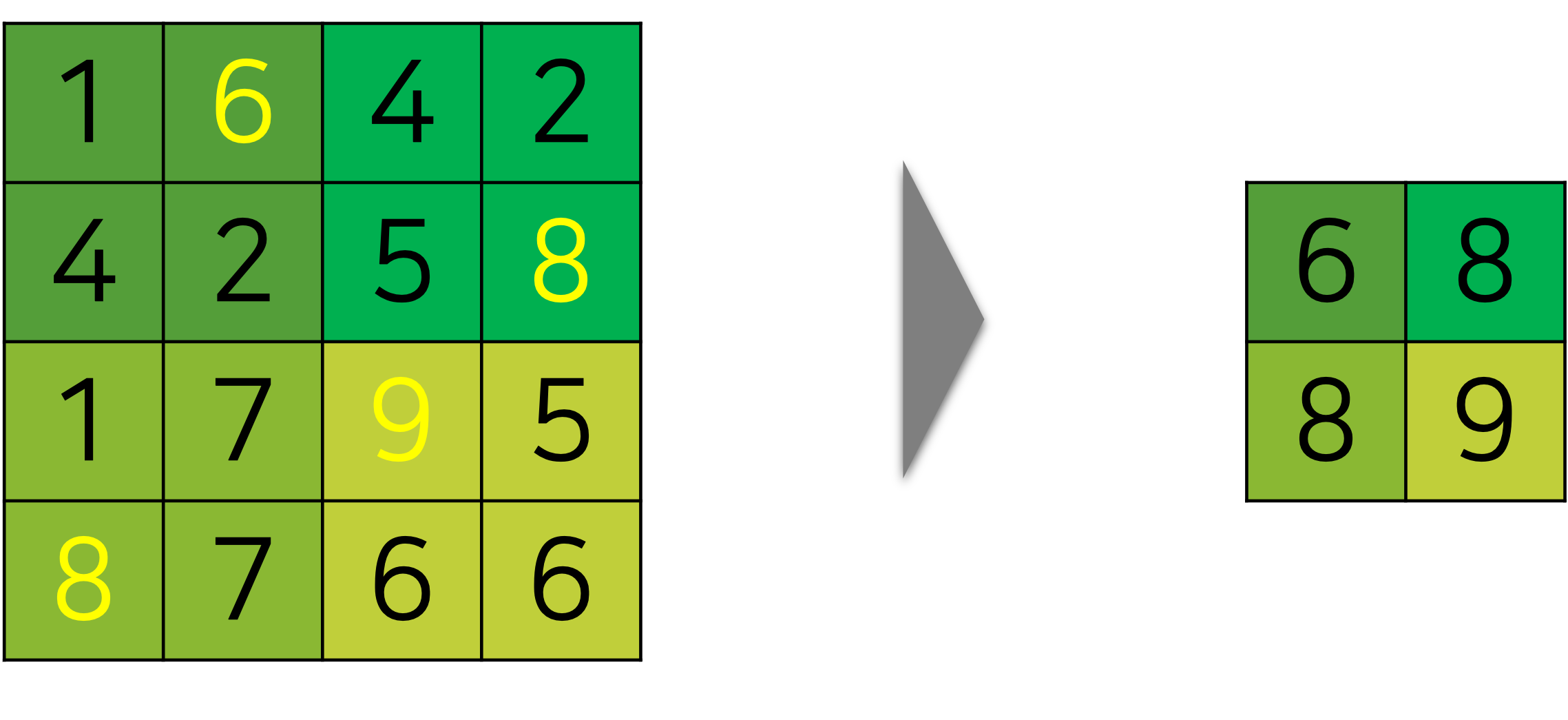
$4\times4$ 크기의 행렬이 크게 4개의 영역으로 나뉘어진 것을 볼 수 있고, 각 영역에서 가장 큰 숫자를 출력하여, $2\times2$ 크기의 행렬에 출력하는 것을 볼 수 있습니다.
만약 이러한 맥스 풀링 함수가 기존의 합성곱 계층의 결과물을 입력으로 받게 된다면 어떤 의미가 될까요? 예를 들어 앞의 그림에서 맥스 풀링 함수의 입력인 $4\times4$ 행렬이 합성곱 계층의 출력물이라고 생각해보도록 하죠. 그리고 그 합성곱 계층은 $3\times3$ 크기의 커널과 $1$ 패딩을 갖고 있다고 가정해보도록 하겠습니다. 그렇다면 합성곱 계층의 입력 행렬의 크기도 $4\times4$ 가 될 것입니다. 이때 합성곱 계층의 출력 행렬의 각 요소는 입력 행렬의 해당 위치에 커널의 패턴이 나타난 강도를 의미한다고 볼 수 있습니다. 만약 값의 크기가 크다면 입력 행렬의 해당 위치에는 커널과 비슷한 패턴이 존재한다고 볼 수 있고, 값의 크기가 작을수록 해당 패턴과 반대되는 패턴이 나타나고 있다고 볼 수 있습니다. 그리고 0에 가까울수록 커널의 패턴과 상관 없는 입력 구성이라고 볼 수 있을 것입니다. 그러므로 합성곱 계층 다음에 맥스 풀링 함수가 가장 큰 값을 가져오는 것은 해당 영역에서 합성곱 계층 커널의 패턴이 얼마나 강하게 있었는지 요약하는 것이라고 볼 수 있습니다.
스트라이드
우리는 맥스 풀링 이외에도 스트라이드stride 기법을 통해 비슷한 형태의 차원 축소를 구현할 수 있습니다. 스트라이드는 그 이름에서 알 수 있듯이, 커널이 기존 방식과 다르게 성큼성큼 칸을 건너뛰어 동작하는 것입니다. 다음 그림들은 스트라이드가 가로 1칸, 세로 1칸 씩 설정되어 커널이 동작하는 모습입니다.
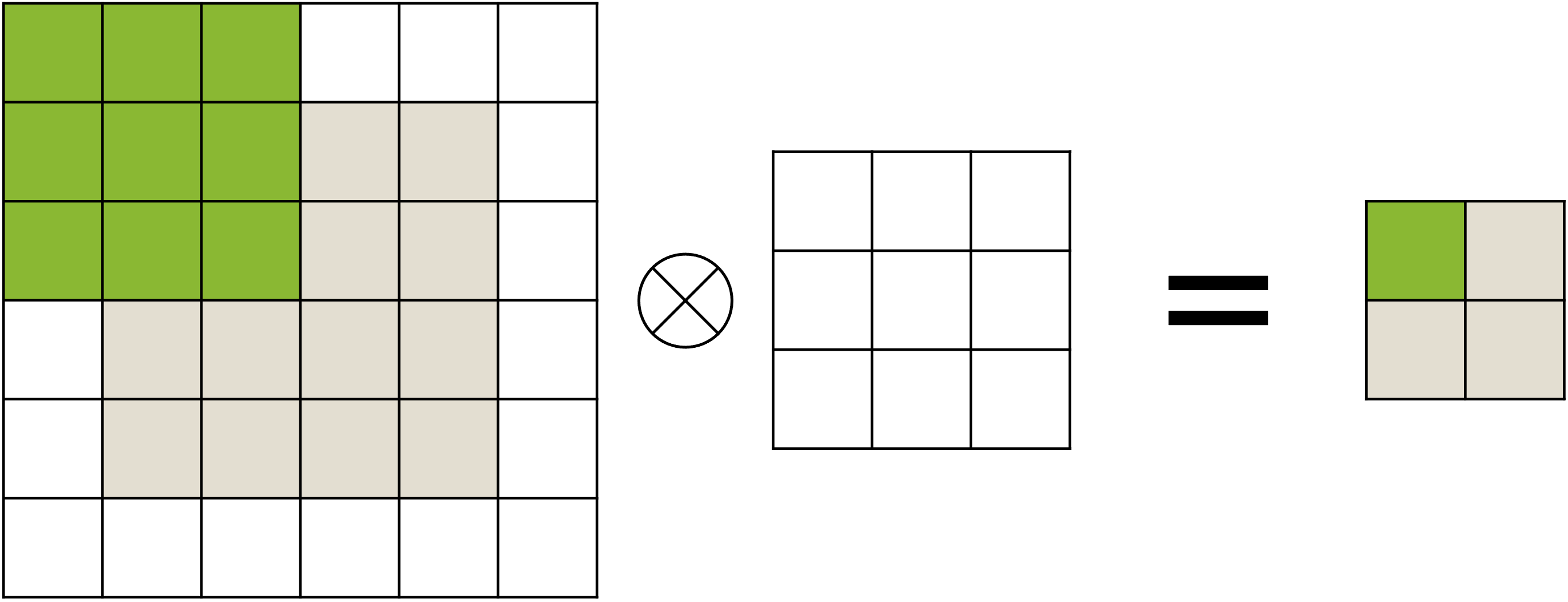

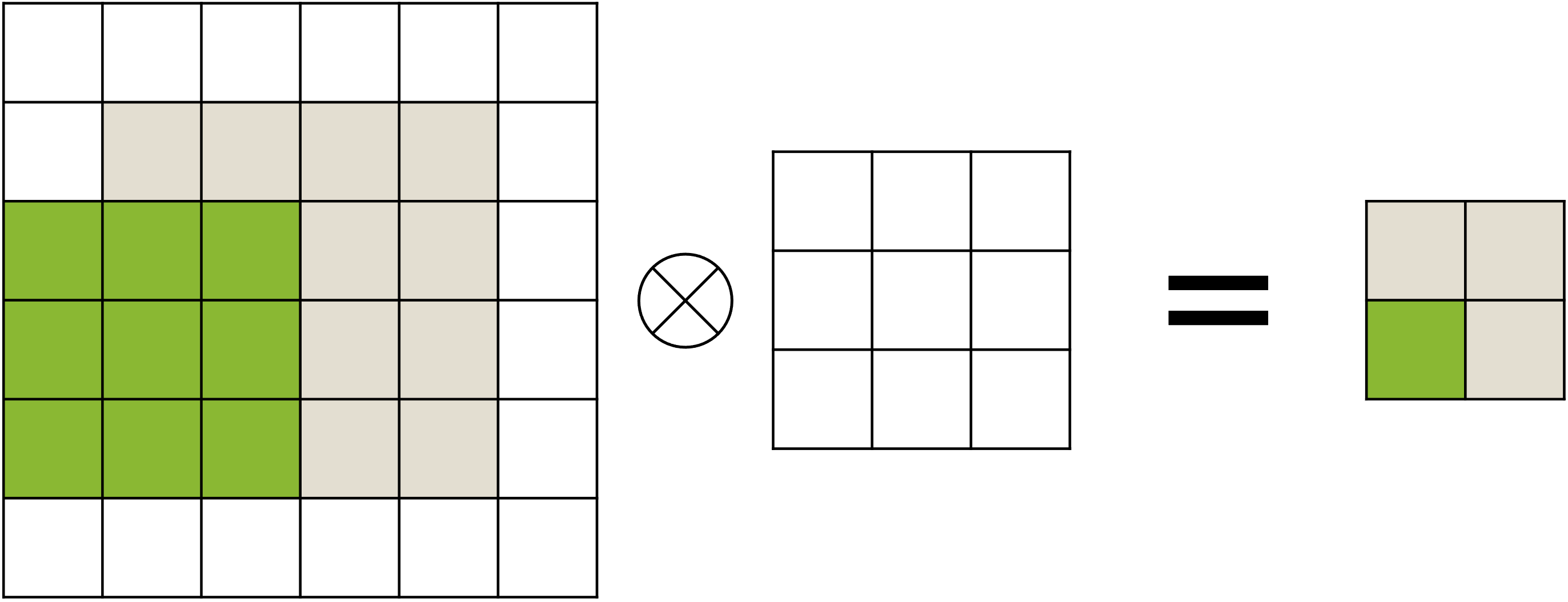

기존과 다르게 가로 세로 한 칸씩을 건너뛰며 합성곱 연산이 수행되었기 때문에, 출력 행렬의 크기가 $2\times2$ 로 줄어든 것을 볼 수 있습니다. 만약 스트라이드가 더 커진다면 입력 대비 출력의 크기는 더욱 줄어들 것입니다.
스트라이드는 코드로 구현할 때 보통 합성곱 계층의 설정 값으로 주어 사용하게 됩니다. 따라서 또 다른 계층이 추가되는 맥스 풀링 기법과 달리, 합성곱 계층 하나로 원하는 작업을 수행할 수 있다는 장점이 있습니다. 하지만 모든 합성곱 연산을 수행한 후, 가장 큰 값을 취해서 요약하는 형태의 맥스 풀링과 달리, 스트라이드 기법은 합성곱 연산 자체를 건너뛰어 버리기 때문에 큰 값을 놓칠 수도 있다는 단점이 존재합니다. 하지만 대부분의 경우 이러한 단점은 실제로 성능에 영향을 끼칠 정도가 될 가능성이 낮아서, 스트라이드를 많이 활용하기도 합니다.
스트라이드 기법이 도입시, 합성곱 계층의 입출력 크기 계산
앞서 우리는 합성곱 계층의 복잡한 입출력 행렬 크기 계산을 살펴보았는데요. 스트라이드 기법을 적용했을 때, 합성곱 계층의 입출력 행렬 크기 계산도 가능합니다. 우리는 다음과 같이 합성곱 계층의 입력 행렬 크기와 채널 갯수, 커널 크기, 패드 크기, 스트라이드 크기가 주어졌을 때, 출력 행렬의 크기를 계산할 수 있습니다.
\[\begin{aligned} N&=\text{batch size} \\ (x_{\text{height}}, x_{\text{width}})&=\text{input size} \\ c_{\text{in}}&=\text{\# input channels} \\ c_{\text{out}}&=\text{\# output channels} \\ (k_{\text{height}}, k_{\text{width}})&=\text{kernel size} \\ (y_{\text{height}}, y_{\text{width}})&=\text{output size} \\ \\ (p_{\text{height}}, p_{\text{width}})&=\text{pad size} \\ (s_{\text{height}}, s_{\text{width}})&=\text{stride size} \\ \end{aligned}\] \[\begin{gathered} y=\text{conv2d}(x), \\ \text{where } \begin{cases} |x|=(N, c_{\text{in}}, x_{\text{height}}, x_{\text{width}}) \\ \begin{aligned} |y|&=(y_{\text{height}}, y_{\text{width}}) \\ &=\Big(N,c_{\text{out}}, \Big\lfloor{\frac{ x_{\text{height}}+2\times{p_{\text{height}}}-(k_{\text{height}}-1)-1 }{ s_{\text{height}} }+1}\Big\rfloor, \Big\lfloor{\frac{ x_{\text{width}}+2\times{p_{\text{width}}}-(k_{\text{width}}-1)-1 }{ s_{\text{width}} }+1}\Big\rfloor \Big). \end{aligned} \end{cases} \end{gathered}\]