LSTM

앞서 다루었던 순환 신경망의 경우에는 순서 데이터를 다룰 수 있다는 특징이 있지만, 치명적인 단점이 있었습니다. 내부에 하이퍼볼릭 탄젠트^{hyperbolic tangent} $\tanh$ 가 존재하여, 그래디언트 소실^{gradient vanishing}이 발생한다는 것입니다. 따라서 긴 순서 데이터를 다룰 경우, 학습 과정에서 그래디언트 소실로 인해 앞 순서 데이터에 대해서는 파라미터 업데이트가 부실해지게 됩니다.^[1] 결과적으로 우리는 기본 RNN을 활용해서 다룰 수 있는 순서 데이터는 짧은 길이로 한정됩니다. 이번에는 이러한 기본 RNN의 단점을 보완하는 LSTM 구조에 대해서 다뤄보도록 하겠습니다.

[1]: RNN은 BPTT^{Back-Propagation Through Time} 기법에 의해서 학습됩니다. 자세한 내용은 저의 온라인 강의를 참고해주세요.

게이트

시그모이드^sigmoid 함수는 전 영역에서 0에서 1사이 값을 반환합니다. 따라서 우리는 특정 값에 시그모이드를 곱하면 마치 문을 열고 닫는 듯한 효과를 낼 수 있습니다. 예를 들어 다음과 같은 수식을 생각해볼 수 있습니다. 여기서 $\otimes$ 는 벡터의 요소별^element-wise 곱셈을 표현합니다.

\[\begin{gathered} f(x)=x\otimes\sigma(W{x}+b) \end{gathered}\]

이 수식을 살펴보면 $x$ 에 시그모이드 함수 결과 값을 곱해주어 값을 취해주는 것을 볼 수 있는데요. 만약 시그모이드 결과 값의 특정 차원이 0에 가깝다면 $x$ 의 해당 차원은 거의 가져올 수 없을 것이고, 시그모이드 결과 값의 특정 차원이 1에 가깝다면 $x$ 의 해당 차원은 대부분 가져올 수 있을 것입니다. 그리고 시그모이드의 입력 값은 선형 계층^{linear layer} 수식으로 되어 있는 것을 볼 수 있는데요. $x$ 의 값에 따라 선형 계층이 큰 값 또는 작은 값을 반환할 것이고, 이것은 시그모이드를 열고 닫는 효과를 내게 됩니다. 우리는 이렇게 동작하는 방식을 게이트^gate라고 부릅니다. 따라서 이 수식에 따라 학습된 게이트는 현재 데이터의 값에 따라 데이터를 통과시킬지말지 여부를 결정하고 행동하게 됩니다.

LSTM 수식

LSTM은 Long Short Term Memory의 약자로 이름에서 알 수 있듯이, 장단기 기억을 수행할 수 있는 구조의 모델입니다. 다음의 그림은 LSTM을 도식화 한 것입니다. 앞서 이야기하였던 게이트가 여러개 존재하는 것을 확인할 수 있습니다.

그림에는 forget 게이트, output 게이트, input 게이트 3개가 존재하는 것을 볼 수 있는데요. 다음의 수식에서도 마찬가지로 확인할 수 있습니다.

\[\begin{aligned} i_t&=\sigma(W_i\cdot[x_t, h_{t-1}]) \\ f_t&=\sigma(W_f\cdot[x_t, h_{t-1}]) \\ g_t&=\text{tanh}(W_g\cdot[x_t, h_{t-1}]) \\ o_t&=\sigma(W_o\cdot[x_t, h_{t-1}]) \\ c_t&=f_t\otimes{c_{t-1}}+i_t\otimes{g_t} \\ h_t&=o_t\otimes\text{tanh}(c_t) \end{aligned}\]

굉장히 복잡한 수식을 가지는 것을 볼 수 있는데요. 이 수식들을 우리가 외우고 있을 필요는 전혀 없습니다. 다만 이 그림과 수식에서 우리가 눈여겨 보아야 할 점은 은닉 상태^{hidden state} $h_t$ 이외에도 셀 상태^{cell state}라는 개념이 추가되었다는 점입니다. 그래서 그림의 왼쪽에서 들어오는 이전 순서의 결과 값은 $h_{t-1}$ 과 $c_{t-1}$ 두 개가 되고, 마찬가지로 이번 순서의 출력 값도 $h_t, c_t$ 두 개가 됩니다.

이러한 구조를 갖는 LSTM은 기존 기본 RNN의 단점인 그래디언트 소실 문제를 해결하였습니다. 따라서 길이가 긴 순서 데이터에 대해서도 훌륭하게 동작하는 장점을 갖습니다. 하지만 보다시피 그 구조가 매우 복잡하고 기본 RNN에 비해서 훨씬 더 많은 파라미터를 갖는다는 단점을 갖습니다.

GRU

앞서 살펴보았던 LSTM은 매우 복잡한 구조를 갖고 있고, 파라미터도 굉장히 많은 편입니다. 따라서 2014년에 제안된 GRU^{Gated Recurrent Unit}는 이러한 LSTM의 단점을 보완하고자 하였습니다. 다음의 그림과 수식은 GRU를 표현한 것입니다.

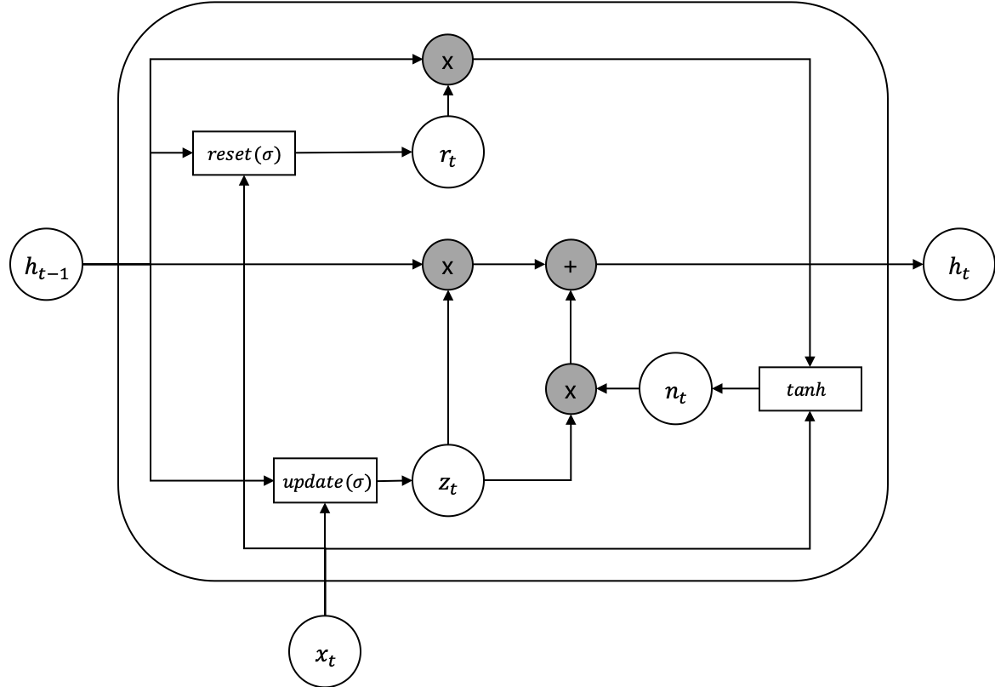
\[\begin{aligned} r_t&=\sigma(W_r\cdot[x_t, h_{t-1}]) \\ z_t&=\sigma(W_z\cdot[x_t, h_{t-1}]) \\ n_t&=\text{tanh}(W_n\cdot[x_t, r_t\otimes{h_{t-1}}]) \\ h_t&=(1-z_t)\otimes{n_t}+z_t\otimes{h_{t-1}} \end{aligned}\]

그림과 수식에서 볼 수 있듯이, 기존의 LSTM에 비해서 훨씬 간결한 구조를 가지고 있습니다. 하지만 여전히 2개의 게이트를 가지고 있고, 사실 이 게이트가 그래디언트 소실을 방지하는데 주요한 역할을 합니다. 더욱이 LSTM에는 셀 상태 $c_t$ 라는 개념이 추가되었던 것에 비해, GRU에서는 여전히 은닉 상태 $h_t$ 하나만 가지고 있어서 실제 구현할 때에도 훨씬 용이합니다. (파이토치로 직접 LSTM이나 GRU를 구현하지는 않지만, 은닉 상태와 셀 상태를 처리하는 코드가 필요한 경우가 종종 있습니다.) 결과적으로 GRU는 더 적은 파라미터를 가지고 그래디언트 소실 문제를 해결하며, LSTM에 비해 성능이 떨어지지도 않습니다.

그렇다면 GRU가 훨씬 더 많이 쓰여야 할 것 같지만, 딱히 LSTM을 대체하지는 못했습니다. 실제로는 LSTM이 좀 더 널리 쓰이는 추세이며, 필자도 GRU를 프로젝트에 활용해 본 경험에 비해 LSTM을 프로젝트에 활용한 경험이 압도적으로 더 많습니다. 딱히 이유가 있는 것은 아니지만, 관행적인 이유가 크지 않을까 생각됩니다.

LSTM의 입출력 텐서 형태

LSTM의 입출력 및 은닉 상태 텐서 모양도 기존 기본 RNN과 똑같습니다. 각 텐서 모양은 다음와 같습니다.

\[\begin{aligned} |\text{input}|&=(\text{batch\_size},n,\text{input\_size}) \\ |\text{output}|&=(\text{batch\_size},n,\#\text{direction}\times\text{hidden\_size}) \\ |\text{hidden\_state}|&=(\#\text{direction}\times\#\text{layers},\text{batch\_size},\text{hidden\_size}) \\ |\text{cell\_state}|&=|\text{hidden\_state}| \end{aligned}\]

셀 상태 텐서의 모양도 은닉 상태 텐서의 모양과 같음에 주목해주세요. 그리고 앞서와 마찬가지로 양방향 LSTM이 될 경우, $#\text{direction}=2$ 일 것입니다. GRU의 경우에도 셀 상태 텐서가 없을 뿐, LSTM과 똑같습니다.

정리

기존의 기본 RNN은 다른 계층들과 달리 순서 데이터를 다루기에 적당한 구조를 지녔지만, 내부에 $\tanh$ 가 있어서 그래디언트 소실 문제를 갖게 되어, 실제로 유용하게 활용되기 어려웠습니다. 하지만 LSTM은 기존 기본 RNN에 비해서 더 많은 파라미터를 갖지만, 그래디언트 소실 문제를 해결하였기에 더 긴 순서 데이터를 다룰 수 있게 되었습니다. 따라서 자연어처리와 같은 순서 데이터를 다루는 분야에서 매우 요긴하게 쓰였는데요. 비록 LSTM의 파라미터가 크게 늘어나서 학습 데이터와 시간이 많이 필요하게 되었지만, 요즘에는 하드웨어의 발달과 데이터의 축적으로 인해서 그런 특징들이 전혀 문제되지 않았기 때문입니다.

하지만 LSTM이 모든 문제를 해결한 것은 아닙니다. 일단 시간 축에 대해서는 그래디언트 소실 문제가 해결 되었지만, LSTM 자체를 여러 층을 깊게 쌓을 때에는 여전히 그래디언트 소실 문제가 발생합니다. 또한 더 큰 문제는 무작정 긴 순서 데이터를 모두 다룰 수 있는 것은 아니라는 점입니다. 왜냐하면 비록 그래디언트 소실 문제는 해결되었을지라도, 신경망의 수용 능력^capacity는 한정되어 있기 때문입니다. 따라서 결국에서는 긴 순서 데이터가 주어짐에 따라 성능이 점점 하락하는 것을 막을 수 없습니다. 결과적으로 이러한 문제를 해결하기 위해서는 어텐션^attention 기법의 도입이 필요하고, 트랜스포머^Transformer가 자연어처리 뿐만 아니라 기타 다른 딥러닝을 활용한 분야를 모두 정복하는 원인 중의 하나가 됩니다.