RNN 한 걸음씩 들여다보기
기본 RNN 구조
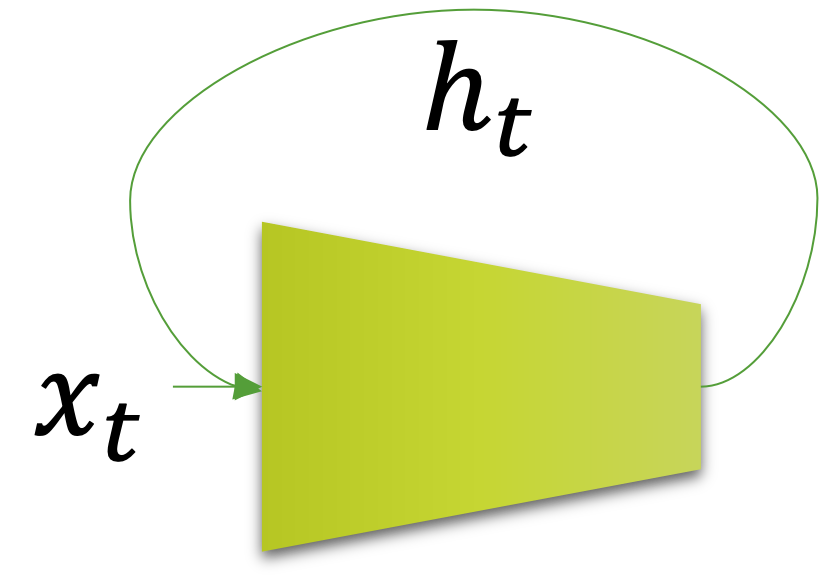
RNN은 다음의 수식과 같이 네 개의 가중치 파라미터weight parameter를 갖습니다.
\[\begin{gathered} \begin{aligned} \hat{y}_t=h_t&=f(x_t,h_{t-1};\theta) \\ &=\tanh(W_{ih}x_t+b_{ih}+W_{hh}h_{t-1}+b_{hh}), \end{aligned} \\ \text{where }\theta=\{W_{ih},b_{ih},W_{hh},b_{hh}\}. \end{gathered}\]$W_{ih},b_{ih}$ 는 입력 $x_t$ 에 곱해지고 더해지는 파라미터가 되고, $W_{hh},b_{hh}$ 는 이전 순서의 결과 값인 $h_{t-1}$ 에 곱해지고 더해지는 파라미터가 됩니다. 그럼 이 연산 결과 값에 하이퍼볼릭 탄젠트hyper-bolic tangent를 통과시켜 현재 순서의 $h_t$ 를 얻을 수 있습니다. 우리는 이 $h_t$ 를 RNN의 은닉 상태hidden state라고 부릅니다. 앞서와 같은 그림을 우리는 시간에 대해서 펼쳐서 표현해볼 수 있습니다. 그럼 다음과 같이 좀 더 이해하기 쉽게 표현될 것입니다.

그럼 이와 같은 RNN을 어떻게 학습시킬 수 있을까요? RNN을 활용 및 학습하는 방법은 여러가지가 있지만, 가장 기본적인 방법은 모든 순서의 결과 값(은닉 상태) $h_t$ 들을 출력으로 취급하여 학습하는 것입니다. 그럼 우리는 정답도 순서 데이터sequential data로 $y={y_1,\cdots,y_T}$ 와 같이 갖고 있어야 할 것입니다. 이에따라 다음 그림과 같이 $h_t\Rightarrow\hat{y}_t$ 가 되어 실제 정답과 비교하는 손실 함수를 구성할 수 있습니다.
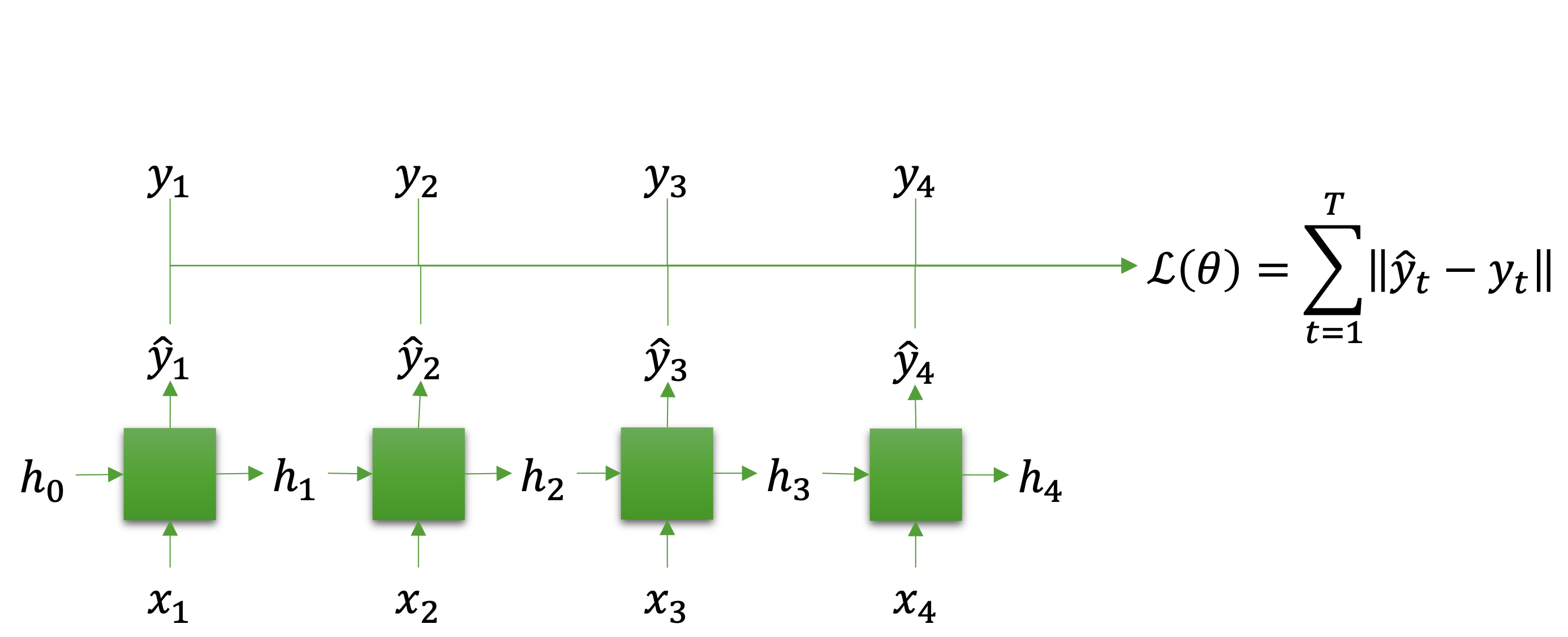
이러한 형태의 RNN을 활용하게 되면 우리는 가변 길이의 순서sequence 데이터를 다룰 수 있게 됩니다. 순서 데이터는 각 순서별 나타나는 값에 따라 앞뒤 순서의 값들이 영향을 받을 뿐만 아니라, 전체 순서 데이터의 의미가 결정되기도 합니다. 순환 신경망은 이러한 가변 길이의 순서 데이터를 잘 다룰수 있으며, 따라서 자연어처리에서 많이 활용됩니다.
RNN의 입출력 텐서 형태
만약 여러분이 RNN을 이해하기 어렵다면, 입출력 텐서 형태만 외우셔도 좋습니다. 어쨌든 디테일한 RNN의 구현은 파이토치가 해결해줄 것이고, 입출력만 잘 맞춰 구현한다면 잘 동작할 것이기 때문입니다. 다음의 그림은 RNN의 입력 텐서의 모양을 시각화 한 것입니다.
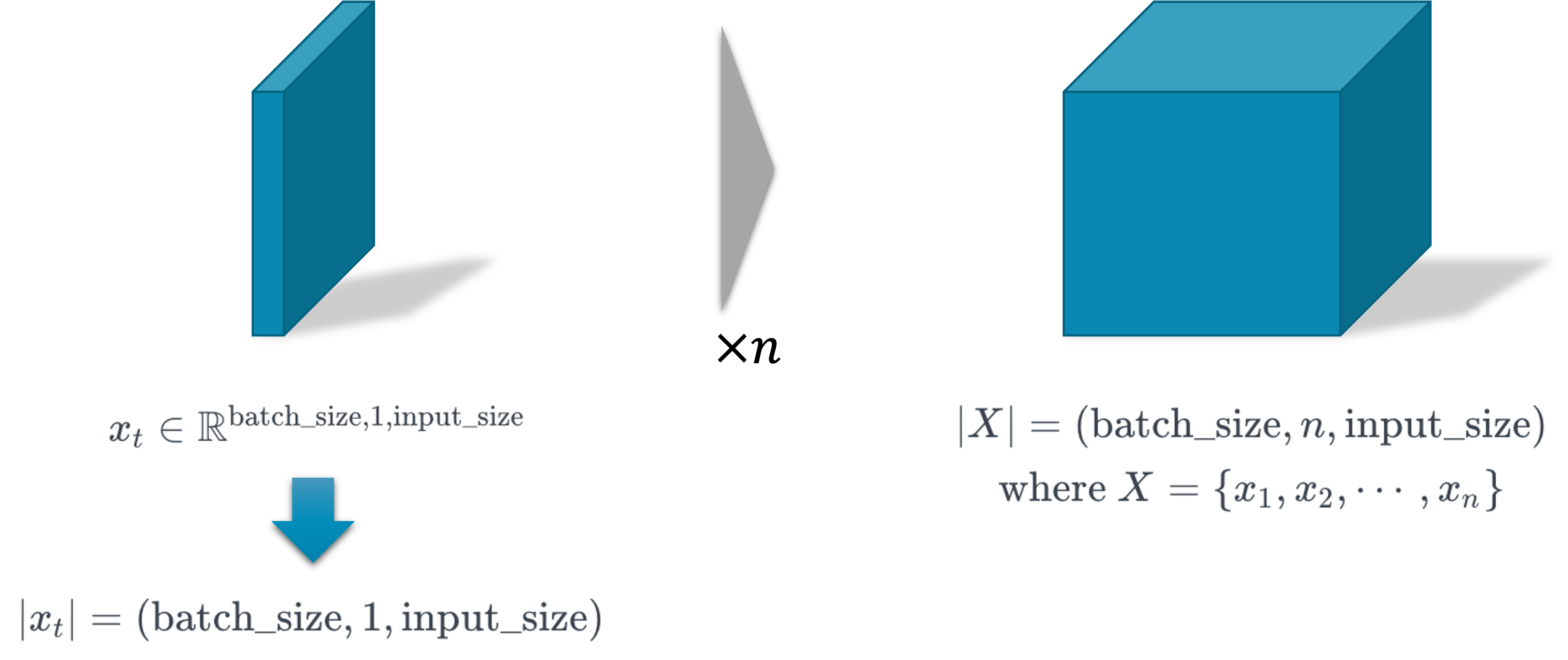
하나의 순서에 대한 텐서를 $x_t$ 라고 할 때 그림의 왼쪽과 같은 텐서가 존재할 것이고, 순서가 $n$ 개 있다면 오른쪽 그림과 같은 텐서가 될 것입니다. 텐서의 첫 번째 차원은 미니배치 내의 인덱스를 가리키고, 두 번째 차원은 순서 정보를 가지며, 마지막 차원은 입력 벡터가 됩니다.
그럼 이와 같은 RNN의 입력이 들어가면 반환되는 출력 텐서에 대해서 살펴보도록 하겠습니다.
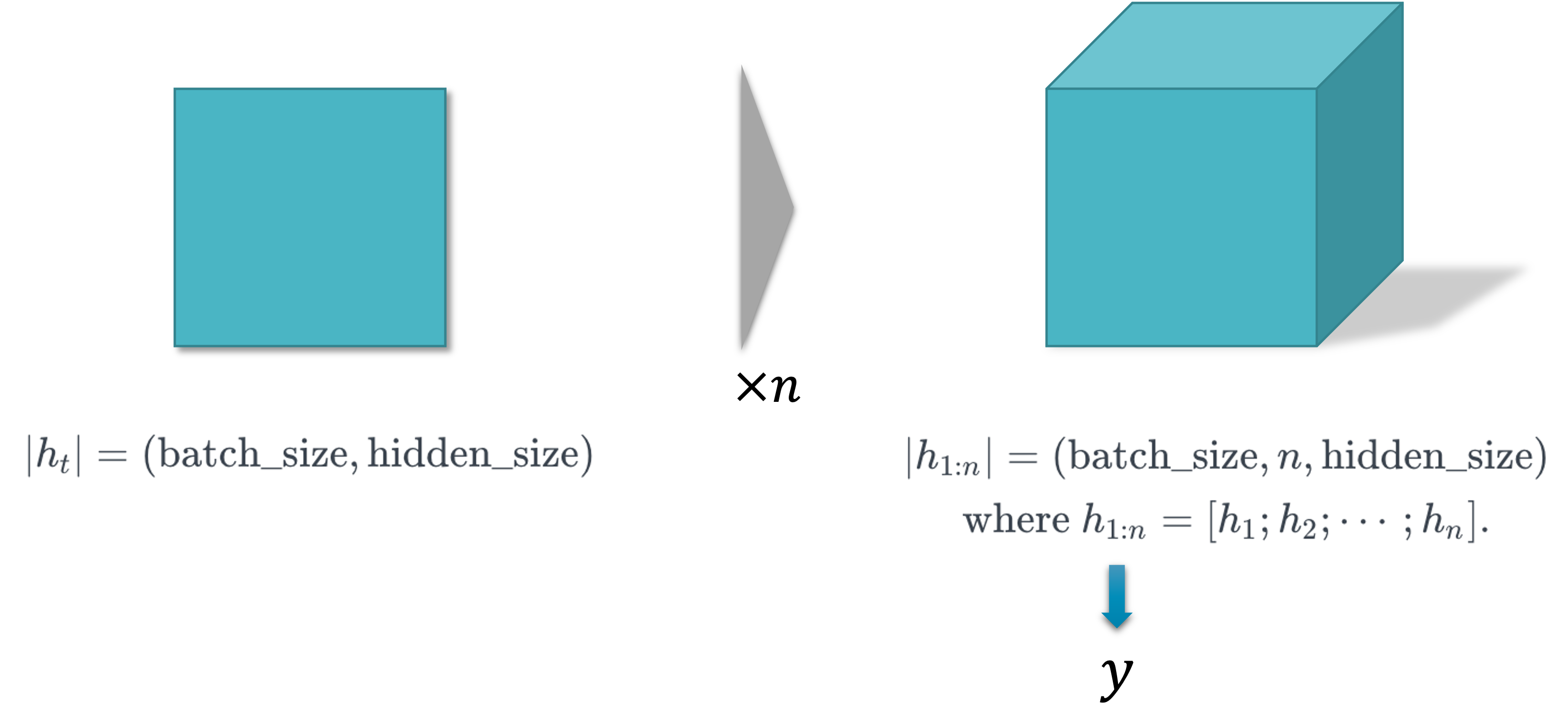
마찬가지로 왼쪽 그림의 텐서들이 모여 오른쪽 그림의 텐서를 이루게 될텐데요. 입력 텐서와 마찬가지로 각 차원들이 똑같은 의미를 지니고 있습니다. 다만 왼쪽 그림에서는 순서 정보에 대한 차원이 빠진 것을 볼 수 있을텐데요. 사실 $(\text{batch_size},\text{hidden_size})=(\text{batch_size},1,\text{hidden_size})$ 이므로 여전히 같은 텐서의 형태라고 보아도 무방합니다. 즉, 왼쪽 텐서들을 모아서 이어붙이기concatenate하면 전체 순서에 대한 출력 $h_{1:n}$ 이 나오게 됩니다.
다계층 순환 신경망
앞서 우리는 선형 계층linear layer이나 합성곱 계층convolutional layer을 여러 층 쌓아서 심층신경망을 만들었던 것처럼, RNN도 여러 층을 쌓아서 깊게 만들 수 있습니다. 이것을 다계층 순환 신경망multi-layered RNN이라고 부릅니다. 다음의 그림은 다계층 순환 신경망을 그림으로 나타낸 것입니다. 마찬가지로 다계층 순환 신경망도 각 순서마다 출력 $\hat{y}_t$ 를 반환하는 것을 볼 수 있고, 실제 정답 $y_t$ 와 비교해서 손실 함수를 계산하는 것을 볼 수 있습니다.
그런데 자세히 보면 각 층마다 오른쪽으로 빠지는 화살표가 나오는 것을 볼 수 있는데요. 앞서 단일 계층 순환 신경망에서 우리는 오른쪽으로 빠지는 화살표를 은닉 상태 $h_t$ 라고 하였고, 이것이 곧 출력 $\hat{y}_t$ 라고 하였습니다. 하지만 다계층 순환 신경망에서는 여러 층이 동시에 $h_t$ 를 반환하기 때문에 $\hat{y}_t\neq{h_t}$ 가 됩니다.
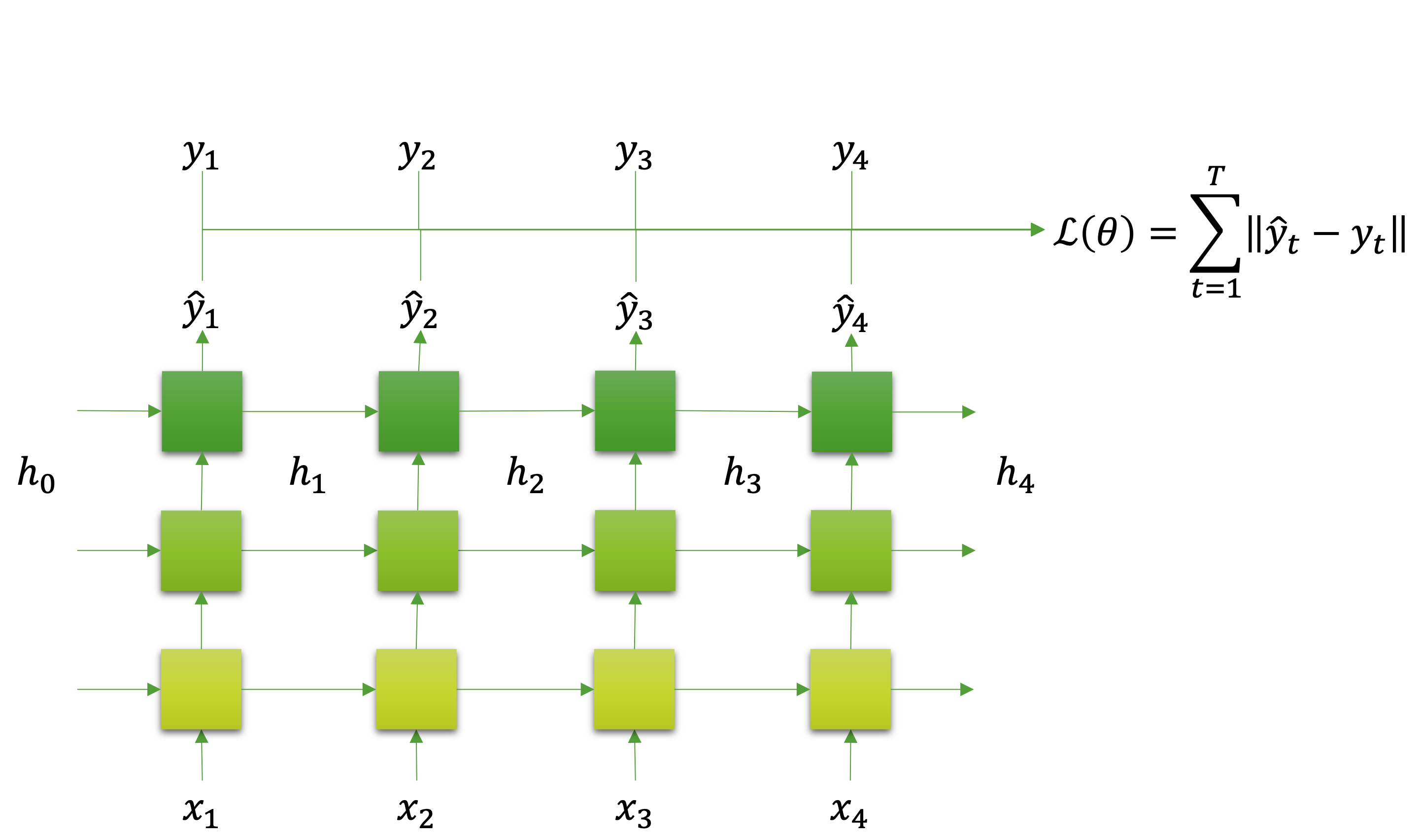
수식을 살펴보아도 각 계층마다 $h_{t,\ell}$ 을 반환하고, 마지막 계층의 $h_{t,\ell}$ 을 받아서 $\hat{y}_t$ 로 삼고 있음을 볼 수 있습니다. 즉, 다계층 순환신경망에서는 은닉 상태hidden state가 모델의 출력이 되지 않습니다. 이와 관련해서는 출력 텐서의 형태를 다룰 때 다시 이야기하도록 하겠습니다.
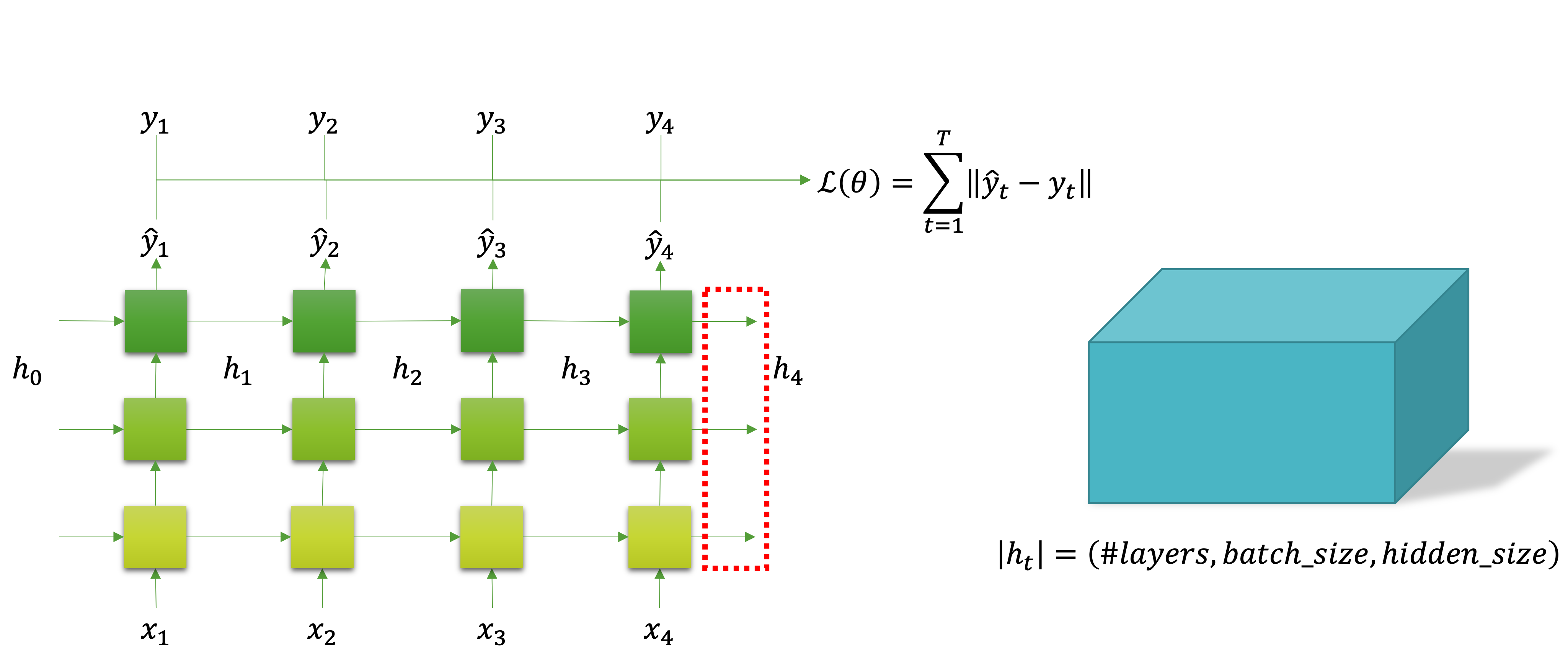
그럼 다계층 순환 신경망의 입출력 텐서 형태를 알아보도록 하겠습니다. 다음의 그림에서 빨간색 점선 네모로 표시된 부분이 다계층 순환 신경망의 입력이 되는 부분입니다.

이때 입력 텐서의 형태는 앞서 보았던 단일 계층 순환 신경망의 입력 텐서의 형태와 같습니다.
그럼 이번에는 다계층 순환 신경망의 출력 텐서에 대해 살펴보도록 하겠습니다. 다음 그림에서 빨간색 점선 네모로 표시된 부분이 출력 텐서에 해당하는 부분입니다.

사실 마찬가지로 단일 계층 순환 신경망의 출력 텐서와 형태가 같습니다. 하지만 중요한 점은 단일 계층 순환 신경망에서는 은닉 상태hidden state가 곧 출력이 되었던 반면, 다계층 순환 신경망에서는 출력과 은닉 상태가 다릅니다. 이것든 다음 그림을 보면 좀 더 정확하게 알 수 있는데요. 다음 그림은 다계층 순환 신경망의 은닉 상태를 빨간색 점선 네모로 표시한 그림입니다.
그림에서 볼 수 있듯이 빨간색 점선 네모의 위치가 달라졌고, 텐서의 모양도 다른 것을 볼 수 있습니다. 가장 주목할 점은 앞서 출력 텐서의 경우에는 순서 정보가 두 번째 차원에 들어가있는 반면에, 은닉 상태 텐서의 경우에는 특정 순서 상에서 얻을 것이기 때문에 순서 정보가 텐서에 없습니다. 대신에 가장 첫 번째 차원이 미니배치와 관련된 정보가 아닌 계층 순서에 대한 정보가 담겨있습니다. 그리고 두 번째 차원에 미니배치에 대한 정보가 담겨있습니다.
은닉 상태
그럼 은닉 상태hidden state에는 어떤 정보가 담겨 있을까요? 은닉 상태에는 순환 신경망이 현재 순서까지 입력 $x_1,\cdots,x_t$ 들을 받아오면서 자신의 상태를 업데이트한 기억을 갖고 있다고 볼 수 있을 것입니다. 당연한 이야기지만 이 은닉 상태는 신경망을 통과하는 값일 뿐이며, 학습하는 가중치 파라미터가 아닙니다.
예를 들어 여러분들과 같은 사람들도 오감(e.g. 시각, 청각, 촉각 등)을 통해서 들어오는 입력들에 따라 생각하고 행동할텐데요. 우리가 입력을 받아 생각하는 것은 가중치 파라미터와 연산을 하는 것이라고 볼 수 있을 것 같습니다. 그리고 행동하는 것은 모델의 출력 $\hat{y}_t$ 라고 볼 수 있을테고, 우리가 기억하는 것이 모델의 은닉 상태 $h_t$ 라고 볼 수 있을 것입니다.
한술 더 떠서 우리의 몸(+뇌 구조)과 똑같은 인조인간을 만든 후, 우리의 기억을 옮기면 우리와 똑같은 존재가 만들어질텐데요. 마찬가지로 똑같은 가중치 파라미터를 갖는 RNN을 만든 후, 이전까지의 은닉 상태를 현재 순서의 입력과 함께 넣어주면, 이전 순서에 이어 잘 동작하는 RNN을 얻을 수 있습니다.
양방향 다계층 순환 신경망
앞서 살펴본 RNN은 한 방향으로만 은닉 상태가 흐르는 모델이었습니다. 즉, 현재 순서의 은닉 상태는 이전 순서의 은닉 상태와 현재 입력에만 의존하게 됩니다. 이러한 모델을 자기회귀auto-regressive 모델이라고 부릅니다. 하지만 이번에는 역방향을 추가된 양방향 순환 신경망bi-directional RNN을 살펴보도록 하겠습니다.
다음 그림은 양방향 다계층 순환 신경망bi-directional multi-layered RNN을 도식화 한 것입니다. 각 층의 RNN 셀cell은 이전 계층의 정방향forward과 역방향backward 결과물을 입력으로 받습니다. 그리고 정방향 RNN 셀은 이전 순서의 은닉 상태를 받고, 역방향 RNN 셀은 미래 순서의 은닉 상태를 받습니다.
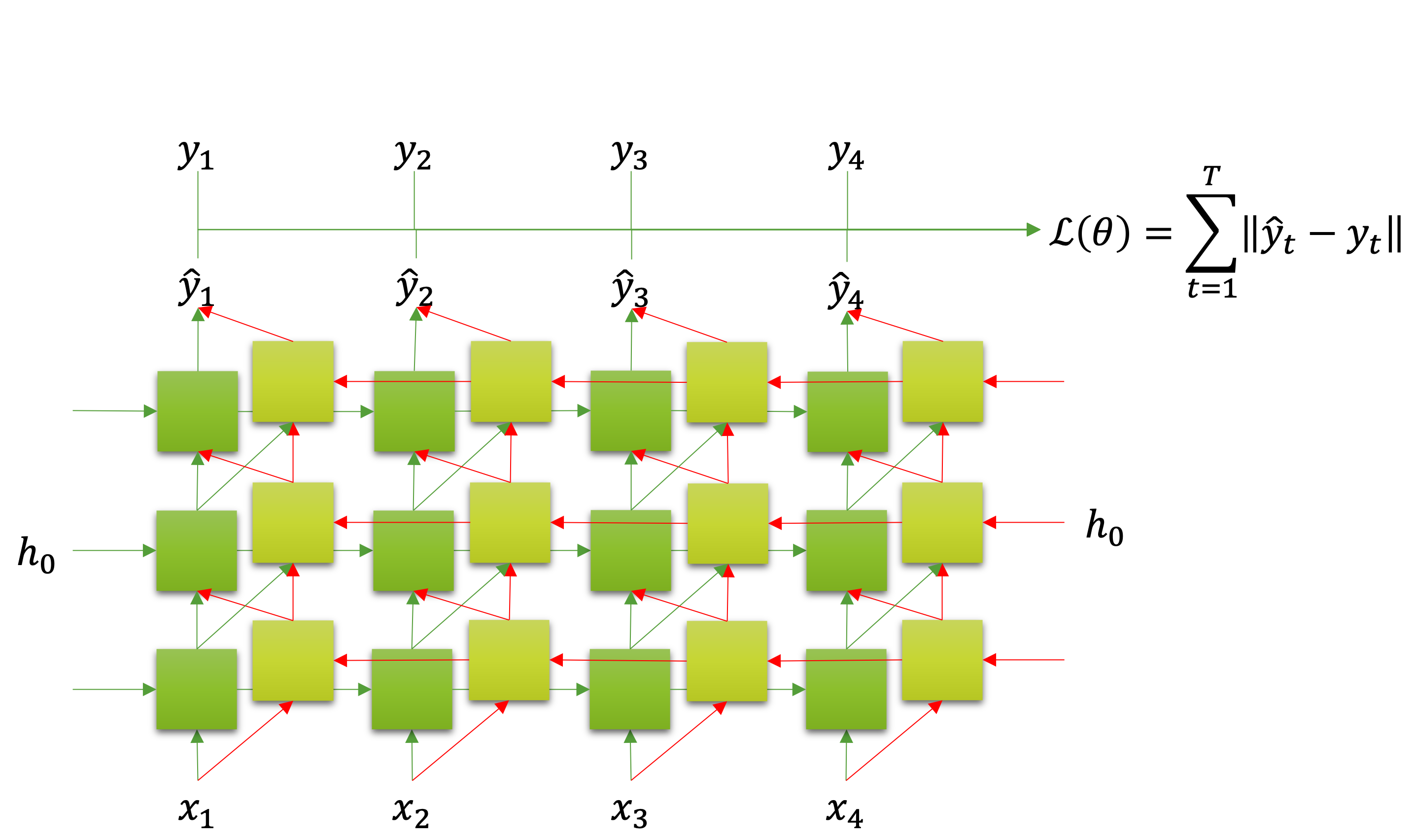
모델의 입력 텐서 모양은 앞서와 살펴보았던 모델들의 입력 텐서 모양과 똑같습니다. 그리고 출력 텐서 모양은 다음의 그림과 같습니다.
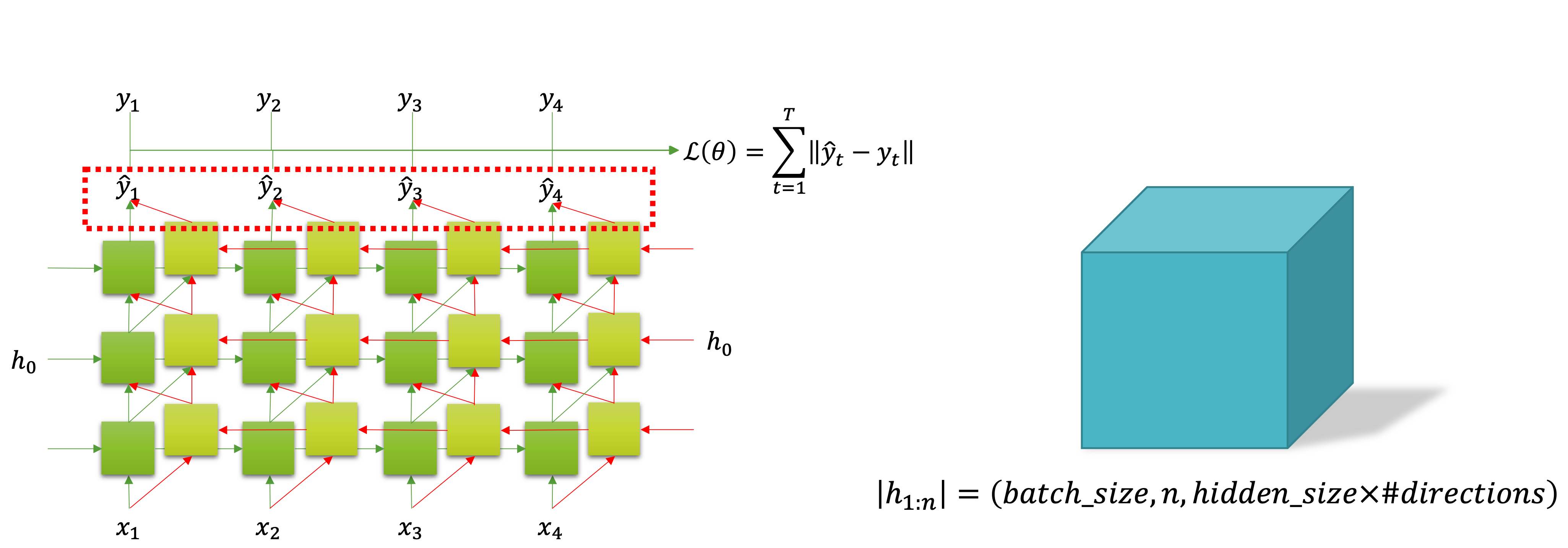
그림의 빨간색 점선 네모로 표시되어 있는 부분에서 알 수 있듯이, 출력 텐서는 마지막 계층의 정방향과 역방향 RNN 셀로부터 출력을 수집합니다. 그래서 텐서의 형태에서 마지막 차원이 $\text{hidden_size}\times\text{#direction}$ 로 되어 기존의 2배가 된 것을 볼 수 있습니다.
양방향 순환 신경망의 은닉 상태는 다루지 않도록 하겠습니다. 보통 단방향 순환 신경망의 경우에는 은닉 상태를 따로 저장했다가 이어서 연산을 진행하는 등의 작업을 수행하는 경우도 많기 때문에 은닉 상태를 직접 다룰 일이 많지만, 양방향 순환 신경망의 경우에는 중간에 은닉 상태를 접근할 일은 거의 없기 때문입니다.