오토인코더

앞서 우리는 선형 차원 축소에 대해 살펴보았습니다. 선형 차원 축소를 통해서 얻어진 특징 벡터는 비선형 데이터의 특징을 잘 표현하지 못한다는 단점이 존재합니다. 이때 비선형 차원 축소를 수행할 수 있는 방법 중에 하나인 오토인코더^autoencoder는 비선형 차원 축소를 수행할 수 있도록 하는 심층신경망입니다.^[1]

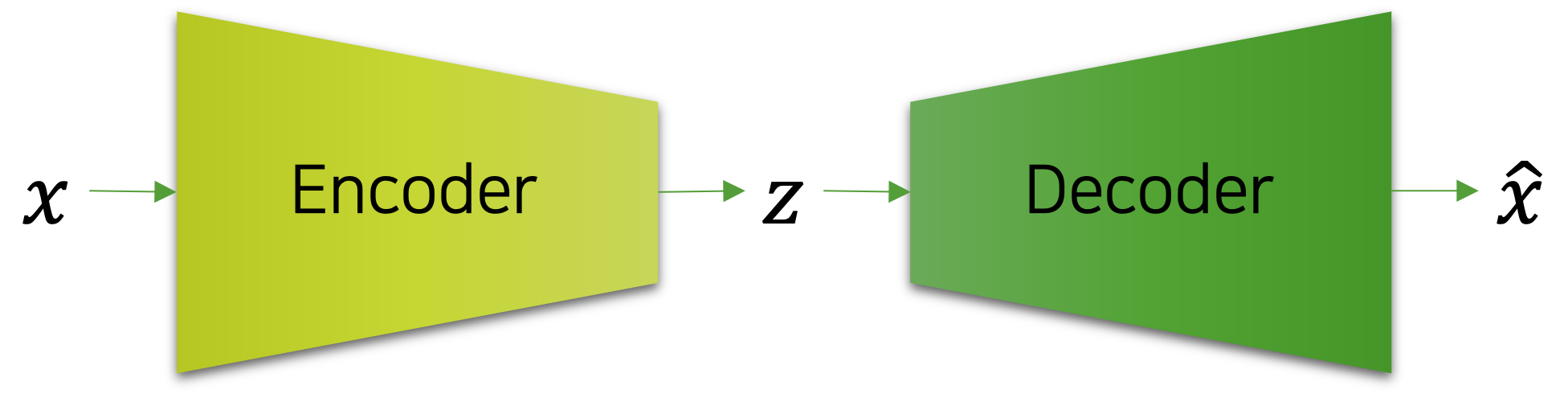
오토인코더는 인코더^encoder와 디코더^decoder로 구성되어 있으며, 인코더를 통해 데이터의 차원 축소과 복원을 수행합니다. 이 과정은 마치 압축과 해제와 같아서, 인코더는 최대한 입력 샘플의 정보를 보존하도록 손실 압축을 진행하고, 디코더는 인코더의 중간 결과물 $z$ 을 받아서 입력 샘플과 같아지도록 압축 해제를 수행합니다. 결과적으로 복원을 성공적으로 진행하기 위해서, 오토인코더는 학습 데이터의 특징^feature을 추출하는 방법을 자동으로 학습하게 됩니다. 참고로 오토인코더는 입력 샘플 $x$ 와 출력 벡터 $\hat{x}$ 의 MSE 손실을 최소화 하도록 학습됩니다.

인코더와 디코더의 역할

인코더는 고차원의 입력을 받아 복원에 필요한 정보를 중심으로 손실 압축을 진행합니다. 그러므로 인코더가 뱉어낸 중간 결과물 $z$ 는 입력 샘플보다 낮은 차원의 벡터입니다. 만약 정보량에 비해 차원이 충분이 크다면 손실 되는 정보가 적어질 것이고, 반대로 차원이 작다면 손실되는 정보가 많아질 것입니다. 이때 효율적인 압축을 수행하기 위해서, 인코더는 중요한 특징이 무엇인지 자동으로 파악하고, 뻔한 정보는 버릴 것입니다. 예를 들어 MNIST 데이터셋의 경우, 좌상단 첫 번째 픽셀의 경우 항상 글씨가 존재하지 않으므로, MNIST 데이터 샘플을 표현하는데 있어서 해당 픽셀에 대한 정보는 필요하지 않습니다.

인코더와 디코더 사이의 병목^bottleneck 구간에 존재하는 인코더의 중간 결과물 $z$ 는 입력 샘플을 최대한 보존하고 있습니다. 따라서 디코더는 주어진 중간 결과물 벡터를 활용하여 입력 샘플을 최대한 복원할 수 있을 것입니다. 그 과정에서 중간 결과물 벡터는 효율적인 압축을 수행해야 하므로, 자연스럽게 고밀도 벡터^{dense vector}로 표현되고 있을 것입니다. 또한 우리는 이 중간 결과물 벡터 또한 입력 샘플에 대한 특징 벡터라고 볼 수 있습니다.^[2]

은닉 표현

우리는 이렇게 얻어진 중간 결과물 벡터 $z$ 를 입력 샘플 $x$ 에 대한 은닉 표현^{hidden(latent) representation}이라고 부릅니다. 그리고 해당 벡터가 존재하는 공간을 은닉 공간^{hidden(latent) space}이라고 부릅니다. 다음의 그림은 MNIST 데이터셋을 은닉 공간에 표현한 것입니다. 여기서 각각의 색깔은 특정 숫자를 의미합니다.^[3]

기존의 특징 벡터들은 각 차원 별로 수치가 의미하는 바가 있었습니다. 예를 들어 MNIST 샘플 벡터의 첫 번째 차원은 좌상단 첫 번째 픽셀의 글씨 존재 유무를 수치로 표현한 것이라고 봐도 될 것입니다. 그렇다면 은닉 벡터^{hidden(latent) vector}의 각 차원은 무엇을 의미할까요? 아쉽게도 우린 알 수 없습니다. 그러므로 은닉이라는 이름이 붙은 것입니다. 다만 앞서 그림에서 볼 수 있듯이, 각 차원이 의미하는 바는 해석할 수 없지만, 비슷한 특징을 갖는 샘플들은 비슷한 값(위치)을 갖는 것을 볼 수 있습니다.

은닉 벡터는 원하는 출력을 뱉어내는데 필요한 정보를 해당 모델만 아는 방법으로 감춰놓고 있습니다. 이것은 꼭 오토인코더에와 같이 입력 샘플을 똑같이 복원하는데에만 적용되는 것이 아니라, 분류와 같은 문제에도 적용됩니다. 예를 들어 MNIST 샘플의 숫자를 분류한다는 관점에서도 필요한 정보는 분명히 존재할 것입니다. 그렇다면 MNIST 분류 모델의 중간 계층의 중간 결과물 벡터는 분류에 필요한 정보를 꼭 담고 있어야 합니다. – 물론 비록 분류를 위한 정보는 샘플을 똑같이 복원하기 위해 필요한 정보보다 훨씬 적을 것입니다.

그리고 해당 중간 결과물 벡터는 아마도 입력 샘플보다 훨씬 작은 차원으로 표현되고 있을 것입니다. 따라서 해당 중간 결과물 벡터도 당연히 입력 샘플에 대한 특징 벡터라고 볼 수 있으며, 물론 은닉 벡터라고도 불릴 수 있을 것입니다. 다음 그림이 이것을 잘 표현해주고 있는데요.

그림에선 3개의 계층이 존재하고, 2개의 은닉 표현 $h_1,h_2$ 가 존재하는 것을 볼 수 있습니다. 또한 입력 벡터 $x$ 의 차원 크기에 비해 은닉 표현이 출력에 가까워질수록 더 작아지는 것을 볼 수 있습니다. 보통은 이처럼 입력에 비해 더 작거나 비슷한 차원을 활용하여 데이터의 비선형 관계를 풀어내도록 모델의 구조를 설계합니다. 따라서 오토인코더의 병목 구간처럼, $x\rightarrow{y}$ 관계를 예측하는데 필요한 정보를 추출할 수 있도록 신경망의 중간 계층들이 학습될 것입니다.

[1]: 만약 비선형활성함수를 제거한다면 PCA와 똑같이 동작합니다.

[2]: 입력 샘플에 대한 임베딩 벡터^{embedding vector}라고 부르기도 합니다.

[3]: 은닉 공간의 벡터 분포는 학습 할 때마다 딥러닝의 학습의 성질 때문에 랜덤하게 바뀌게 됩니다.