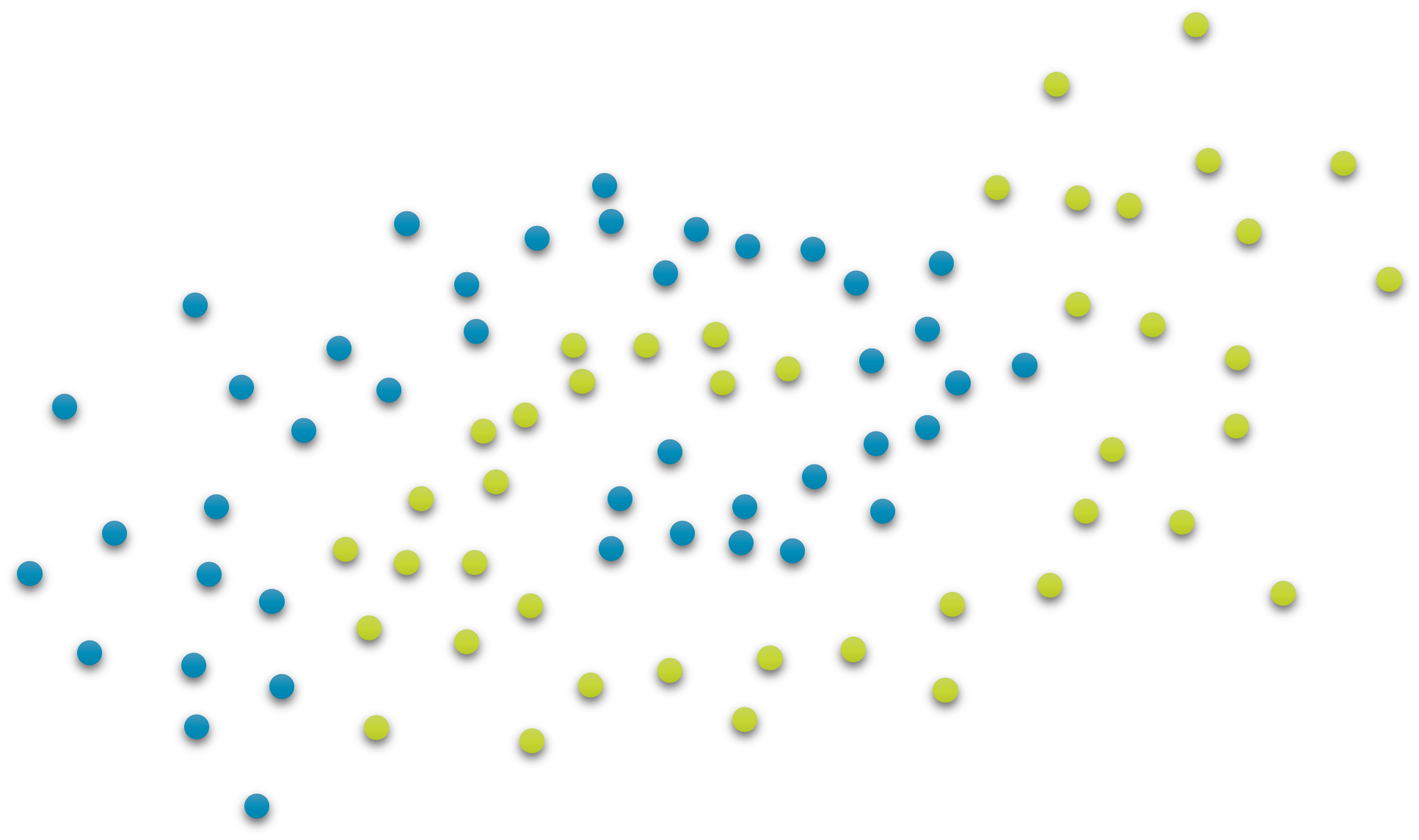
차원 축소

앞서 우리는 특징 벡터^{feature vector}와 희소 벡터^{sparse vector}에 대해서 이야기하였습니다. 희소 벡터는 차원의 대부분이 0인 벡터를 이르는데, 여러 비효율적인 성질을 가지고 있습니다. 이러한 희소 벡터는 우리가 흔히 접할 수 있는데요. 다음의 그림의 MNIST도 일부 희소 벡터의 성질을 가진다고 볼 수 있습니다.

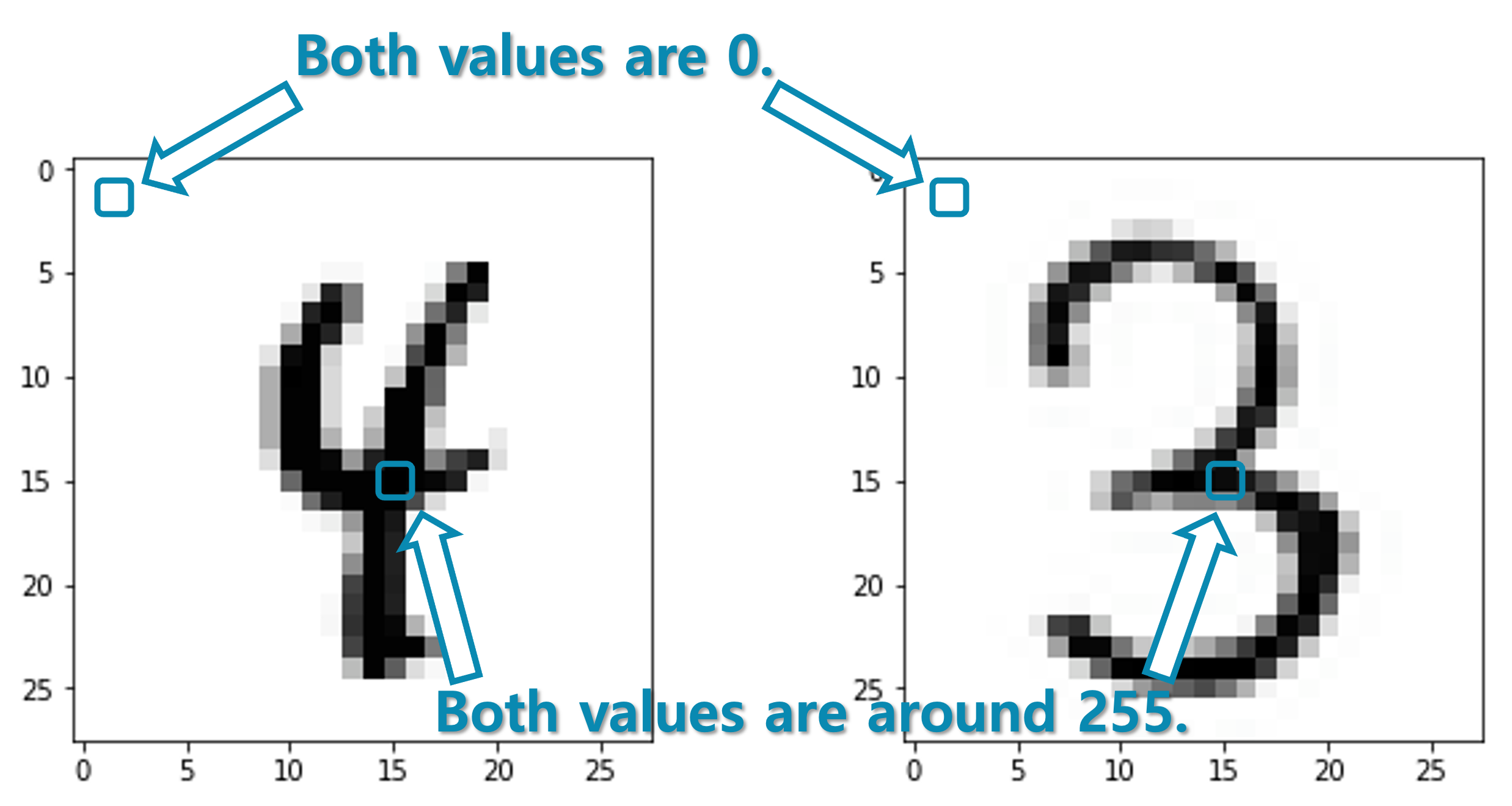
글씨가 존재하는 부분은 255에 가까운 값을 가지게 되고 빈 공간은 0으로 표시되고 있기 때문에, 그림을 한 줄씩 잘라 이어붙여 벡터로 만든다면 많은 차원이 0을 갖는 벡터가 될 것입니다. 특히 글씨는 굉장히 전형적인 위치에 존재하기 때문에, 예를 들어 그림의 좌상단 끝에 위치하는 픽셀은 거의 항상 0을 가리키게 될 것입니다. 다시 말하면, MNIST 데이터의 샘플들이 존재하는 $28\times28=784$ 차원의 공간의 대부분은 비어있고, 일부 영역에만 샘플들이 존재하고 있다고 볼 수 있습니다. 예를 들어, 좌상단 첫 번째 픽셀은 없어져도 샘플들을 분류하는데에는 전혀 지장이 없습니다. 그럼 굳이 784차원의 공간에서 이 데이터를 표현할 필요가 있을까요?

선형 차원 축소: 주성분분석(PCA)

앞서와 같은 필요의 의해서 등장한 방법이 바로 주성분분석^{Principal Component Analysis, PCA}입니다. PCA는 가장 널리 사용되는 차원 축소 방법 중의 하나로, 고차원의 공간에 샘플들이 분포하고 있을 때, 분포를 잘 설명하는 새로운 축^axis를 찾아내는 과정입니다. 이를 통해 우리는 선형 차원 축소^{linear dimension reduction}을 수행할 수 있습니다. 차원 축소를 수행하면 앞서와 같이 희소한 벡터들이 존재할 때, 좀 더 밀도 높은 표현의 벡터로 나타낼 수 있게 될 것입니다.

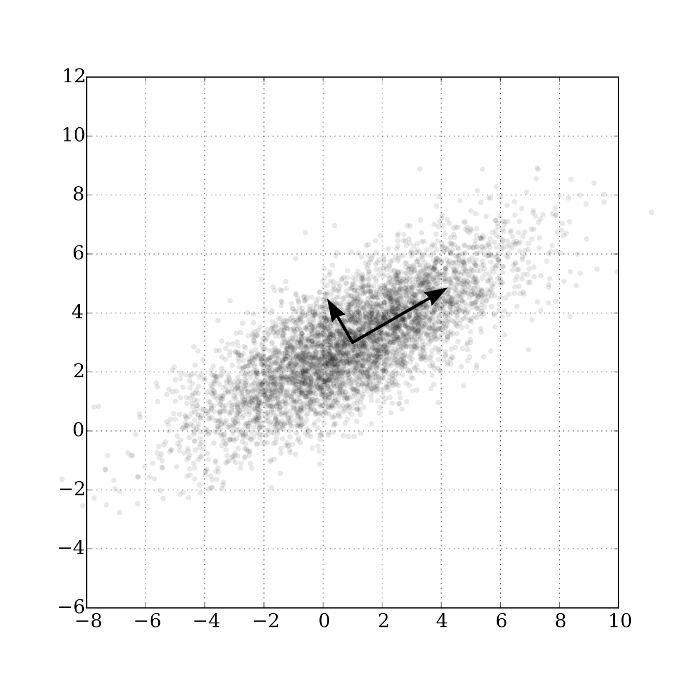
다음의 그림과 같이, 주어진 데이터 샘플들에 대해 두 가지 조건을 만족하는 축을 찾아, 해당 축에 샘플들을 투사^projection하면 낮은 차원의 샘플들로 변환이 가능합니다.

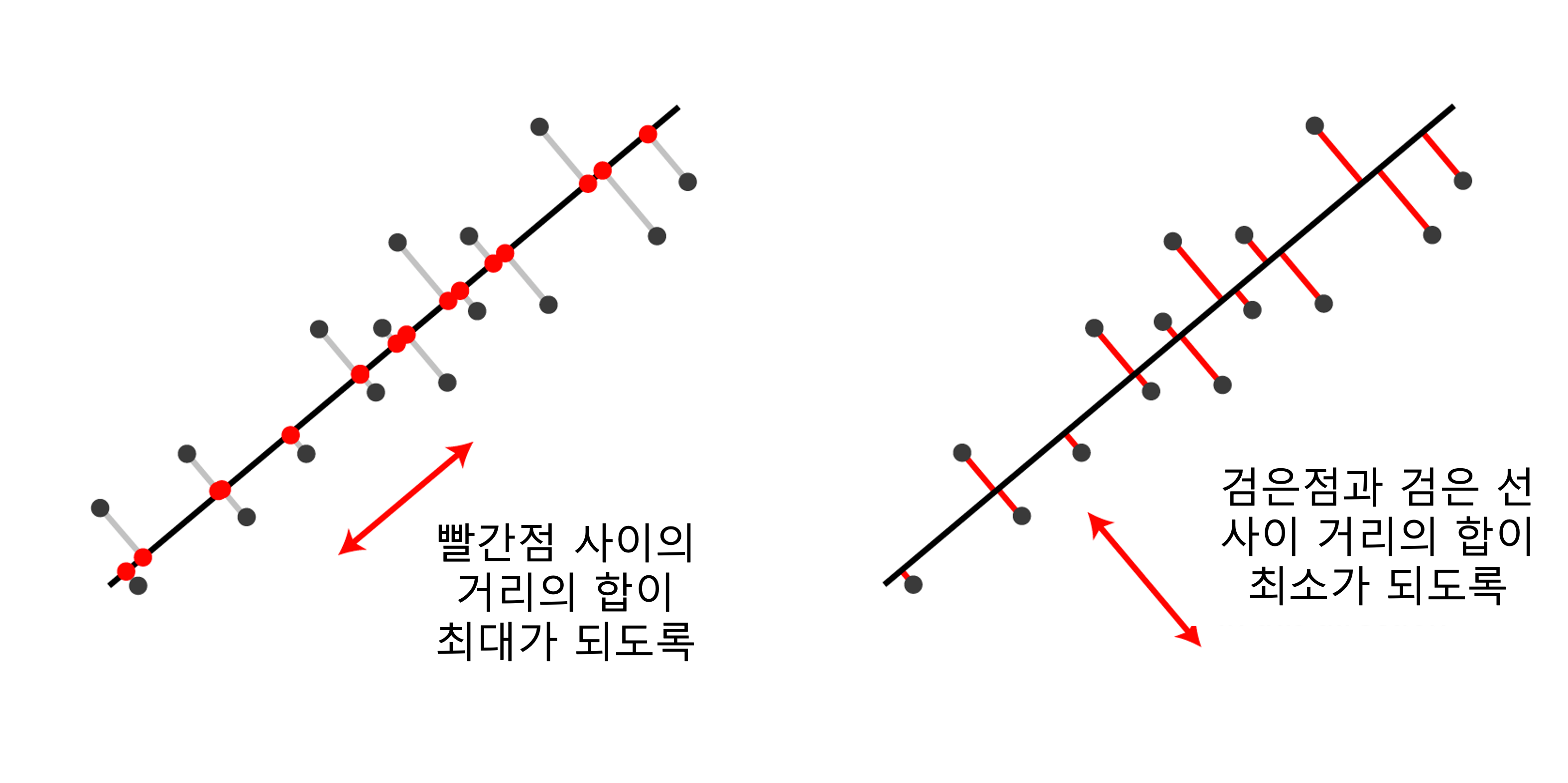
이때 새롭게 찾아낸 축에 투사된 샘플들의 분산이 클 수록 샘플들 사이의 특징을 잘 표현할 수 있으며, 투사하는 거리가 작아질 수록 잃어버리는 정보가 줄어들게 됩니다. PCA를 통해 성공적인 차원 축소를 수행하면, 다음의 그림과 같이 두 그룹을 분리하는 경계선^{dicision boundary}도 성공적으로 찾아낼 수 있을 것입니다.

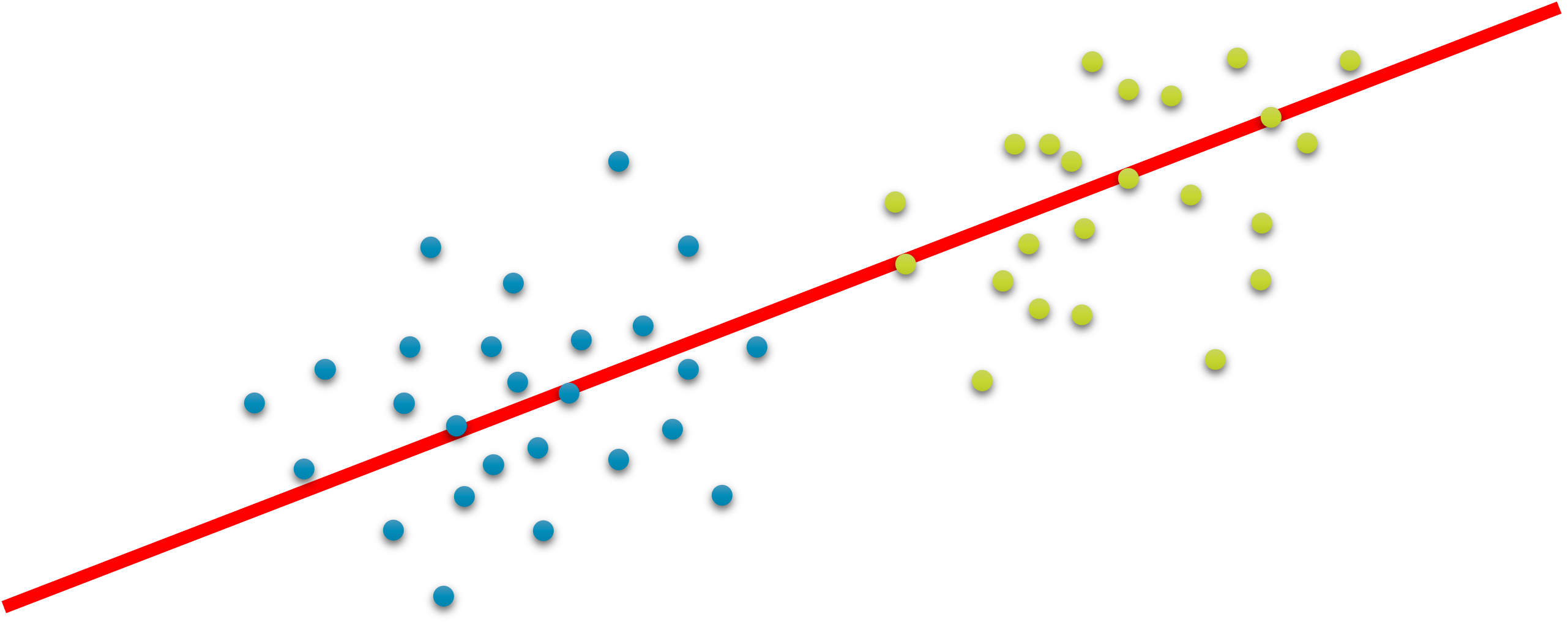
다만, PCA의 경우에는 선형적으로 차원 축소를 수행하기 때문에, 다음의 그림과 같이 비선형적인 경계선을 갖는 경우에는 PCA를 통해 분류를 잘 수행할 수 없습니다. 이러한 케이스들을 해결하기 위해서는, 선형 차원 축소를 뛰어 넘어 비선형 차원 축소를 도입해야 합니다.

---