원 핫 인코딩

앞서 우리는 특징이란 무엇인가에 대해 이야기하고, 특징 벡터를 구성하는 방법에 대해 이야기하였습니다. 이번에는 연속 데이터와 이산 데이터로 구성된 특징들에 대해 이야기하고, 원 핫 인코딩에 대해 배우도록 합니다.

연속 vs 카테고리 값

우리가 다루는 데이터 샘플은 보통 연속 값^{continuous value}과 카테고리 값^{categorical value} 두 가지로 구성됩니다. 연속 값은 보통 키, 몸무게와 같은 실수^{real number} 값으로 표현될 수 있는 값들이 됩니다. 그리고 카테고리 값은 보통 이산 값으로 단어나 클래스로 표현됩니다. 연속 값과 카테고리 값의 결정적인 차이점은, 연속 값은 비슷한 값이라면 비슷한 의미를 지니지만, 카테고리 값은 비슷한 값일지라도 상관 없는 의미를 지닌다는 것입니다.

예를 들어 다음과 같이 단어는 카테고리 값에 속하고, 이것을 사전에 넣어 인덱스^index 값으로 표현해볼 수 있습니다.

사실 우리는 현실 세계에서 볼펜과 연필의 관계는 연필과 자의 관계보다 가깝다는 것을 알고 있습니다.

\[\begin{gathered} \text{distance}(\text{연필},\text{볼펜})<\text{distance}(\text{연필},\text{자}) \end{gathered}\]

하지만 임의로 부여된 인덱스 값을 놓고 보았을 때, 인덱스를 활용하여 계산한 거리는 우리의 상식과 다름을 볼 수 있습니다.

\[\begin{gathered} |\text{연필}-\text{볼펜}|=4>1=|\text{연필}-\text{자}| \end{gathered}\]

그러므로 우리는 카테고리 값을 특징 벡터로 표현할 때, 인덱스 값으로 표기하는 대신 다른 방법을 택해야 합니다. 만약 그대로 인덱스 값으로 나타낸다면, 코사인 유사도^{cosine similarity}나 유클리디안 거리^{Euclidean distance}에서 이상한 계산이 이루어질 것이기 때문입니다.

원 핫 인코딩

이때 사용되는 방법이 원 핫 인코딩^{one-hot encoding}입니다. 크기가 의미를 갖는 정수^integer로 나타내는 방법 대신, 한 개의 1과 $n-1$ 개의 0으로 이루어진 $n$ 차원의 벡터를 의미합니다.

앞의 테이블에서처럼, 공책은 단순이 인덱스 1로 표현되기보단, $n=16$ 차원의 벡터로 표현하되, 두 번째 차원이 1인 것을 볼 수 있습니다. 이렇게 구성된 각각의 원 핫 벡터들은 서로 직교^orthogonal하는 것을 알 수 있습니다. 서로 다른 두 벡터 사이의 코사인 유사도는 항상 0이며, 유클리디안 거리는 $\sqrt{2}$ 인 것을 알 수 있습니다.

이처럼 벡터 대부분의 차원이 0인 경우를 희소 벡터^{sparse vector}라고 부릅니다. 그리고 이의 반대되는 개념은 고밀도 벡터^{dense vector}라고 부릅니다. 앞서 살펴본 것처럼 희소 벡터의 경우, 유사도 계산이나 거리 계산을 통해 샘플 사이의 관계를 파악하는데 어려움을 겪을 수 있습니다. 그리고 원 핫 벡터의 경우에는 희소 벡터의 정점에 있다고 볼 수 있습니다.

단어 임베딩

자연어처리는 단어를 데이터로 다루는 대표적인 분야입니다. 따라서 단어를 모델에 입력으로 넣어주기 위해서 어쩔 수 없이 원 핫 인코딩 벡터를 활용해야 합니다. 하지만 단어의 갯수는 몇 만 개 수준으로 매우 많아 차원이 커져서 비효율 적일 뿐더러, 원 핫 인코딩을 통해서는 단어 사이의 유사도를 표현할 수 없습니다. 분명히 ‘빨강’이라는 단어는 ‘분홍’이라는 단어와 유사한 데, 두 관계는 ‘빨강’과 ‘파랑’ 사이의 관계보다 가깝다는 것을 알 수 없습니다.

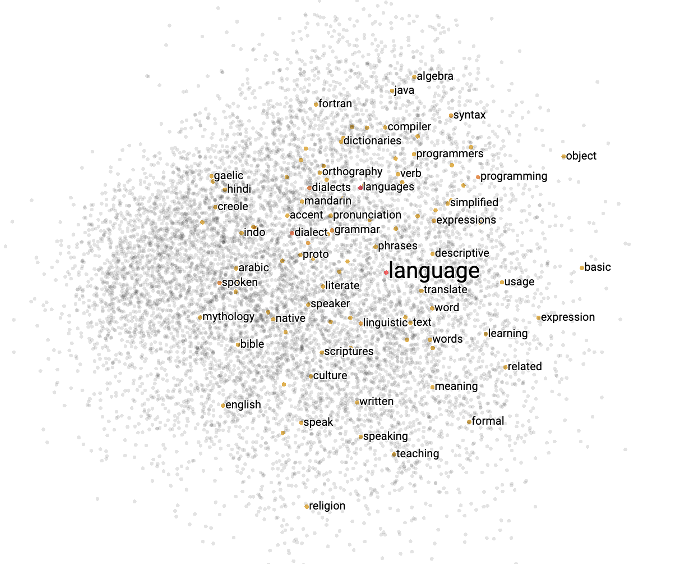
이 때 필요한 것이 단어 임베딩^{word embedding}입니다. 우리는 단어 임베딩 기법^[1]을 통해 원 핫 벡터로 표현된 단어를 고밀도 벡터로 표현할 수 있게 됩니다. 다음의 그림처럼, 고밀도 벡터로 표현된 단어들은 서로 비슷한 단어끼리 비슷한 값을 지니게 됩니다.

[1]: Word2Vec과 같은 방법을 사용할 수도 있고, 임베딩 계층^{embedding layer}을 활용할 수도 있습니다.

---