실습: Regularization

데이터 준비

이번 챕터에서도 MNIST 데이터셋을 활용하여 정규화^{reguarlization} 실습을 진행해보도록 하겠습니다. 앞서 딥러닝을 활용한 분류 문제 실습에서도 MNIST 데이터셋에 대해서 진행하였었는데, 과연 성능이 오르는지 확인해보도록 하겠습니다. 대부분의 코드들은 앞선 챕터에서 구현된 코드들과 동일합니다. 동일한 부분들에 대해서는 자세한 설명은 생략하도록 하겠습니다.

필요한 라이브러리들을 불러옵니다.

import numpy as np
from copy import deepcopy
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

from torchvision import datasets, transforms

MNIST 데이터셋을 불러옵니다. 만약 정해진 위치에 데이터가 없다면 자동으로 다운로드 할 것입니다. 그럼 60,000장의 학습 샘플과 10,000장의 테스트 샘플을 각각 불러올 수 있습니다.

train = datasets.MNIST(
    '../data', train=True, download=True,
    transform=transforms.Compose([
        transforms.ToTensor(),
    ]),
)
test = datasets.MNIST(
    '../data', train=False,
    transform=transforms.Compose([
        transforms.ToTensor(),
    ]),
)

x = train.data.float() / 255.
y = train.targets

x = x.view(x.size(0), -1)
print(x.shape, y.shape)

input_size = x.size(-1)
output_size = int(max(y)) + 1

print('input_size: %d, output_size: %d' % (input_size, output_size))

중요한 점은 이전 실습에서와 같이 2차원 이미지 행렬을 1차원 벡터로 변환했다는 것입니다. 따라서 학습 데이터의 입력과 출력 텐서 크기는 다음과 같습니다.

torch.Size([60000, 784]) torch.Size([60000])
input_size: 784, output_size: 10

MNIST는 테스트 데이터셋이 이미 정해져 있기 때문에, 학습 데이터셋을 학습과 검증 데이터셋으로 나누기만 하면 됩니다. 따라서 8:2의 비율로 나누도록 합니다.

# Train / Valid ratio
ratios = [.8, .2]

train_cnt = int(x.size(0) * ratios[0])
valid_cnt = int(x.size(0) * ratios[1])
test_cnt = len(test.data)
cnts = [train_cnt, valid_cnt]

print("Train %d / Valid %d / Test %d samples." % (train_cnt, valid_cnt, test_cnt))

indices = torch.randperm(x.size(0))

x = torch.index_select(x, dim=0, index=indices)
y = torch.index_select(y, dim=0, index=indices)

x = list(x.split(cnts, dim=0))
y = list(y.split(cnts, dim=0))

x += [(test.data.float() / 255.).view(test_cnt, -1)]
y += [test.targets]

for x_i, y_i in zip(x, y):
    print(x_i.size(), y_i.size())

그럼 48,000장의 학습 샘플과 12,000장의 검증 샘플, 그리고 10,000장의 테스트 샘플로 데이터셋이 구성됩니다.

Train 48000 / Valid 12000 / Test 10000 samples.
torch.Size([48000, 784]) torch.Size([48000])
torch.Size([12000, 784]) torch.Size([12000])
torch.Size([10000, 784]) torch.Size([10000])

학습 코드 구현

앞서의 실습에서는 대부분 nn.Sequential에 원하는 계층과 활성함수를 집어넣어 쉽고 간편하게 모델을 구현할 수 있었습니다. 이번에도 비슷하게 진행할 수 있지만, 한 단계 발전된 방향으로 나아가고자 합니다. 사실 생각해보면 앞서의 실습들에서 활용된 모델들도 선형 계층^{linear layer}과 비선형 활성 함수^{non-linear activation function}의 반복이었습니다. 즉, 하나의 층이 선형 계층과 비선형 활성 함수의 조합으로 이루어지게 되고, 이것을 전체 모듈에 대한 부분 모듈 또는 서브 모듈로 볼 수 있습니다. 그럼 서브 모듈이 입출력 크기만 바뀌어서 반복되고 있던 것으로 볼 수 있습니다. 이번에는 여기에 정규화 계층이 더해져 “선형 계층 + 비선형 활성 함수 + 정규화 계층”이 하나의 서브 모듈이 될 것이고, 마찬가지로 입출력 크기만 바뀌어서 반복 사용되는 것입니다. 그럼 이것에 착안하여 서브 모듈을 nn.Module을 상속받아 하나의 클래스로 정의하고, nn.Sequential에 “선형 계층 + 비선형 활성 함수 + 정규화 계층”을 각각 인자로 넣어주는 대신에, 정의한 클래스 객체를 넣어주면 될 것입니다.

다음 코드는 서브 모듈 클래스를 정의하는 코드입니다. 이 모듈은 생성시에 배치 정규화^{batch normalization}와 드랍아웃^dropout 중에서 선택받고, 입출력 크기를 입력받습니다. 그래서 self.block에 선형 계층, 리키 렐루, 정규화 계층을 nn.Sequential에 넣어 가지고 있습니다. 배치 정규화를 사용한 경우에는 앞서 사용된 선형 계층의 출력 크기를 넣어주어야 하고, 드랍아웃의 경우에는 확률 값을 넣어주어야 합니다. 그리고 forward 함수에서 피드포워드를 구현해줍니다.

class Block(nn.Module):
    
    def __init__(self,
                 input_size,
                 output_size,
                 use_batch_norm=True,
                 dropout_p=.4):
        self.input_size = input_size
        self.output_size = output_size
        self.use_batch_norm = use_batch_norm
        self.dropout_p = dropout_p
        
        super().__init__()
        
        def get_regularizer(use_batch_norm, size):
            return nn.BatchNorm1d(size) if use_batch_norm else nn.Dropout(dropout_p)
        
        self.block = nn.Sequential(
            nn.Linear(input_size, output_size),
            nn.LeakyReLU(),
            get_regularizer(use_batch_norm, output_size),
        )
        
    def forward(self, x):
        # |x| = (batch_size, input_size)
        y = self.block(x)
        # |y| = (batch_size, output_size)
        
        return y

이렇게 정의된 Block 클래스를 곧이어 정의할 MyModel 클래스에서 활용할 계획입니다. 다음의 코드는 MyModel 클래스를 정의한 코드로, nn.Module을 상속받아 만들었습니다. 마찬가지로 init 함수에서 필요한 객체들을 미리 선언해주는데, self.layer는 nn.Sequential 객체를 가지고 있고, 그 내부는 Block 클래스 객체들로 채워져 있습니다. 이전 챕터의 실습과 똑같이 784(input_size) -> 500 -> 400 -> 300 -> 200 -> 100 -> 50 -> 10(output_size) 으로 이어지도록 구성되어 있고, 마지막에는 로그소프트맥스가 위치합니다.

class MyModel(nn.Module):
    
    def __init__(self,
                 input_size,
                 output_size,
                 use_batch_norm=True,
                 dropout_p=.4):
        
        super().__init__()
        
        self.layers = nn.Sequential(
            Block(input_size, 500, use_batch_norm, dropout_p),
            Block(500, 400, use_batch_norm, dropout_p),
            Block(400, 300, use_batch_norm, dropout_p),
            Block(300, 200, use_batch_norm, dropout_p),
            Block(200, 100, use_batch_norm, dropout_p),
            Block(100, 50, use_batch_norm, dropout_p),
            nn.Linear(50, output_size),
            nn.LogSoftmax(dim=-1),
        )
        
    def forward(self, x):
        # |x| = (batch_size, input_size)        
        y = self.layers(x)
        # |y| = (batch_size, output_size)
        
        return y

MyModel 모델 객체를 선언하고 프린트해보도록 합니다.

model = MyModel(input_size,
                output_size,
                use_batch_norm=True)

print(model)

모델을 프린트해보면 기존에 비해 조금 내용이 길어졌지만, 보기 좋게 서브 모듈들이 나뉘어져 반복되고 있는 것을 볼 수 있습니다.

MyModel(
  (layers): Sequential(
    (0): Block(
      (block): Sequential(
        (0): Linear(in_features=784, out_features=500, bias=True)
        (1): LeakyReLU(negative_slope=0.01)
        (2): BatchNorm1d(500, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): Block(
      (block): Sequential(
        (0): Linear(in_features=500, out_features=400, bias=True)
        (1): LeakyReLU(negative_slope=0.01)
        (2): BatchNorm1d(400, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (2): Block(
      (block): Sequential(
        (0): Linear(in_features=400, out_features=300, bias=True)
        (1): LeakyReLU(negative_slope=0.01)
        (2): BatchNorm1d(300, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (3): Block(
      (block): Sequential(
        (0): Linear(in_features=300, out_features=200, bias=True)
        (1): LeakyReLU(negative_slope=0.01)
        (2): BatchNorm1d(200, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (4): Block(
      (block): Sequential(
        (0): Linear(in_features=200, out_features=100, bias=True)
        (1): LeakyReLU(negative_slope=0.01)
        (2): BatchNorm1d(100, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (5): Block(
      (block): Sequential(
        (0): Linear(in_features=100, out_features=50, bias=True)
        (1): LeakyReLU(negative_slope=0.01)
        (2): BatchNorm1d(50, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (6): Linear(in_features=50, out_features=10, bias=True)
    (7): LogSoftmax(dim=-1)
  )
)

그리고 모델 가중치 파라미터를 아담^Adam 옵티마이저에 등록하고, NLL 손실 함수를 선언합니다.

optimizer = optim.Adam(model.parameters())
crit = nn.NLLLoss()

CUDA가 활용 가능할 경우 GPU가 기본 디바이스가 되도록 device 변수에 집어넣어주고, 이를 활용하여 모델과 텐서를 원하는 디바이스로 이동 및 복사 합니다.

device = torch.device('cpu')
if torch.cuda.is_available():
    device = torch.device('cuda')

model = model.to(device)

x = [x_i.to(device) for x_i in x]
y = [y_i.to(device) for y_i in y]

학습에 필요한 하이퍼 파라미터 및 변수들을 미리 초기화 합니다.

n_epochs = 1000
batch_size = 256
print_interval = 10

lowest_loss = np.inf
best_model = None

early_stop = 50
lowest_epoch = np.inf

다음은 학습을 위한 코드입니다. 똑같은 코드가 계속해서 쓰이고 있습니다. 설명은 생략하도록 하겠습니다.

train_history, valid_history = [], []

for i in range(n_epochs):
    model.train()
    
    indices = torch.randperm(x[0].size(0)).to(device)
    x_ = torch.index_select(x[0], dim=0, index=indices)
    y_ = torch.index_select(y[0], dim=0, index=indices)
    
    x_ = x_.split(batch_size, dim=0)
    y_ = y_.split(batch_size, dim=0)
    
    train_loss, valid_loss = 0, 0
    y_hat = []
    
    for x_i, y_i in zip(x_, y_):
        y_hat_i = model(x_i)
        loss = crit(y_hat_i, y_i.squeeze())

        optimizer.zero_grad()
        loss.backward()

        optimizer.step()        
        train_loss += float(loss)

    train_loss = train_loss / len(x_)
        
    model.eval()
    with torch.no_grad():
        x_ = x[1].split(batch_size, dim=0)
        y_ = y[1].split(batch_size, dim=0)
        
        valid_loss = 0
        
        for x_i, y_i in zip(x_, y_):
            y_hat_i = model(x_i)
            loss = crit(y_hat_i, y_i.squeeze())
            
            valid_loss += float(loss)
            
            y_hat += [y_hat_i]
            
    valid_loss = valid_loss / len(x_)
    
    train_history += [train_loss]
    valid_history += [valid_loss]
        
    if (i + 1) % print_interval == 0:
        print('Epoch %d: train loss=%.4e  valid_loss=%.4e  lowest_loss=%.4e' % (
            i + 1,
            train_loss,
            valid_loss,
            lowest_loss,
        ))
        
    if valid_loss <= lowest_loss:
        lowest_loss = valid_loss
        lowest_epoch = i
        
        best_model = deepcopy(model.state_dict())
    else:
        if early_stop > 0 and lowest_epoch + early_stop < i + 1:
            print("There is no improvement during last %d epochs." % early_stop)
            break

print("The best validation loss from epoch %d: %.4e" % (lowest_epoch + 1, lowest_loss))
model.load_state_dict(best_model)

학습 코드를 실행하면 다음과 같은 학습 결과를 얻을 수 있습니다.

Epoch 10: train loss=2.2342e-02  valid_loss=7.7366e-02  lowest_loss=6.9548e-02
Epoch 20: train loss=1.0553e-02  valid_loss=7.4174e-02  lowest_loss=6.7155e-02
Epoch 30: train loss=8.6981e-03  valid_loss=8.2112e-02  lowest_loss=6.7155e-02
Epoch 40: train loss=5.7398e-03  valid_loss=8.4239e-02  lowest_loss=6.7155e-02
Epoch 50: train loss=6.5757e-03  valid_loss=7.6408e-02  lowest_loss=6.7155e-02
Epoch 60: train loss=3.4350e-03  valid_loss=7.8569e-02  lowest_loss=6.7155e-02
There is no improvement during last 50 epochs.
The best validation loss from epoch 16: 6.7155e-02

16번째 에포크에서 최소 검증 손실 값을 얻었음을 볼 수 있고, 학습 손실 값은 계속해서 낮아지며 오버피팅이 진행되고 있는 것을 확인할 수 있습니다. 앞서 챕터에서 진행되었던 MNIST 분류에 비해 더 낮은 검증 손실 값을 얻은 것을 확인할 수 있습니다.

손실 곡선 확인

plot_from = 0

plt.figure(figsize=(20, 10))
plt.grid(True)
plt.title("Train / Valid Loss History")
plt.plot(
    range(plot_from, len(train_history)), train_history[plot_from:],
    range(plot_from, len(valid_history)), valid_history[plot_from:],
)
plt.yscale('log')
plt.show()

손실 곡선을 그려보면 앞서 프린트 된 내용과 같이 학습 손실 곡선은 계속해서 내려가는 것을 볼 수 있고, 검증 손실 곡선은 16 에포크 이후부터 천천히 올라가는 것을 볼 수 있습니다.

결과 확인

과연 테스트셋에 대해서도 이전 챕터보다 더 좋은 성능이 나왔을까요?

test_loss = 0
y_hat = []

model.eval()
with torch.no_grad():
    x_ = x[-1].split(batch_size, dim=0)
    y_ = y[-1].split(batch_size, dim=0)

    for x_i, y_i in zip(x_, y_):
        y_hat_i = model(x_i)
        loss = crit(y_hat_i, y_i.squeeze())

        test_loss += loss # Gradient is already detached.

        y_hat += [y_hat_i]

test_loss = test_loss / len(x_)
y_hat = torch.cat(y_hat, dim=0)

print("Test Loss: %.4e" % test_loss)

correct_cnt = (y[-1].squeeze() == torch.argmax(y_hat, dim=-1)).sum()
total_cnt = float(y[-1].size(0))

print('Test Accuracy: %.4f' % (correct_cnt / total_cnt))

이전 챕터의 실습 결과에 비해 훨씬 더 좋은 결과가 나오는 것을 볼 수 있습니다.

Test loss: 6.8407e-02
Test Accuracy: 0.9832

그럼 지난 챕터 대비 얼마나 성능이 좋아졌을까요? 단순히 성능의 개선폭을 보는 것은 좋은 방법이 아닐 수 있습니다. 예를 들어 성능 60%의 모델이 70%로 개선되는 것보다, 97%의 모델이 98%로 개선되는 것이 더 좋은 것임을 알고 있습니다. 이때 우리는 ERR^{Error Reduction Rate}을 통해 상대적인 모델의 개선 폭을 측정할 수 있습니다. 지난 챕터 대비 이번 챕터에서 상승한 성능을 비교하면 다음과 같습니다.

\[\begin{aligned} \text{ERR}&=\frac{(1-0.9757)-(1-0.9832)}{1-0.9757} \\ &=\frac{0.0243-0.0168}{0.0243} \\ &=\frac{0.0075}{0.0243}=0.3086 \end{aligned}\]

지난 챕터 대비 오류가 약 31% 줄어든 것을 볼 수 있습니다. 물론 지금은 지난 챕터의 실습과 이번 챕터의 실습 모두 각 한 번 씩만 돌린 것이기 때문에 적절한 비교라고는 볼 수 없습니다. 만약 제대로 비교하고자 한다면, 최소한 5번 이상 같은 실험을 반복하여 평균 테스트 정확도를 측정한 후, ERR을 계산해볼 수 있을 것입니다.

import pandas as pd
from sklearn.metrics import confusion_matrix

pd.DataFrame(confusion_matrix(y[-1], torch.argmax(y_hat, dim=-1)),
             index=['true_%d' % i for i in range(10)],
             columns=['pred_%d' % i for i in range(10)])

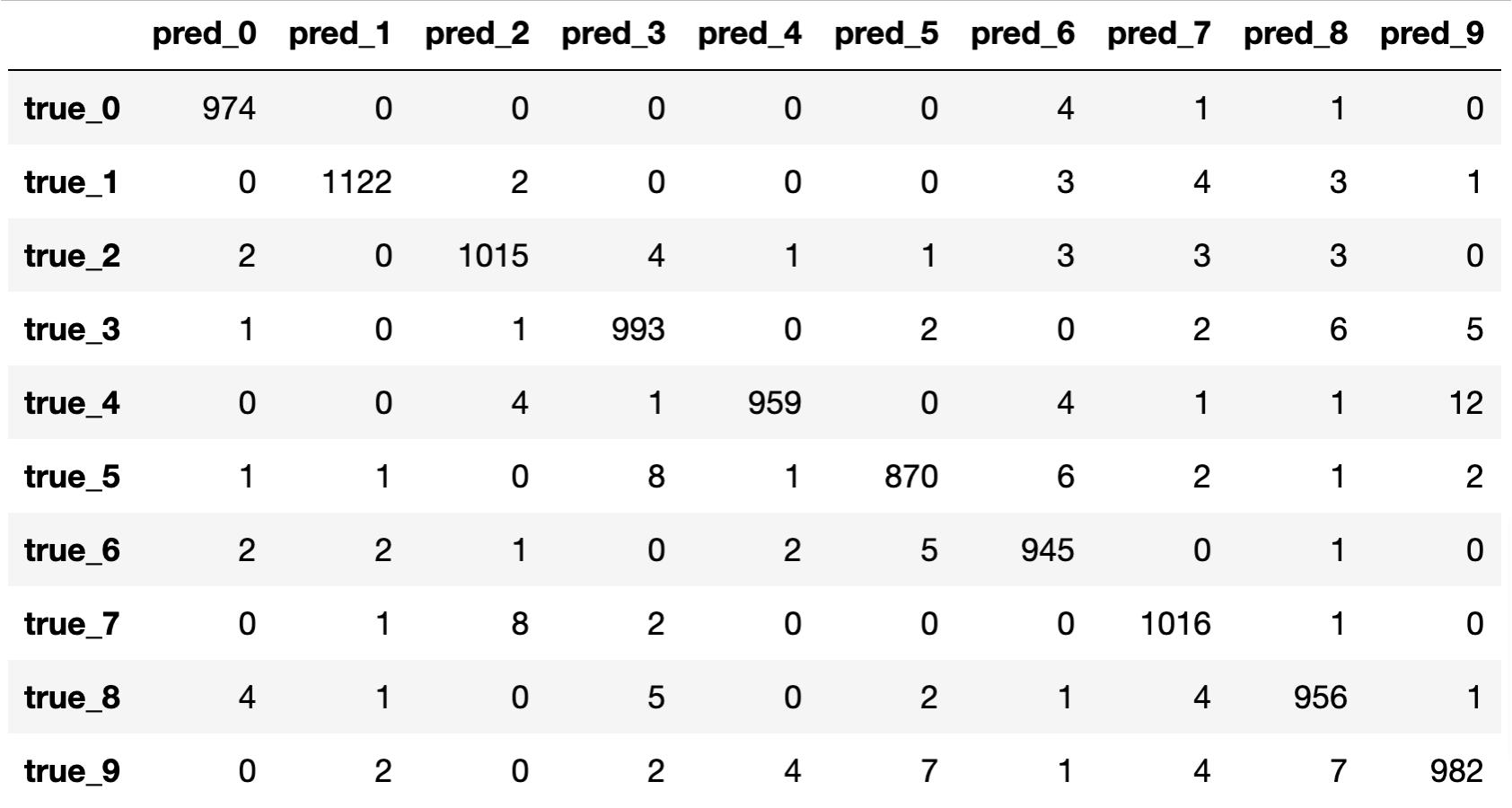
혼동 행렬^{confusion matrix}을 살펴보면, 역시 이전 챕터에 비해 대각 성분의 값이 더 커지고 나머지 값들은 줄어든 것을 확인할 수 있습니다. 그나마 현재 모델의 가장 큰 약점은 4를 9로 잘못 예측하는 경우가 가끔 있다는 점이라고 볼 수 있습니다.

이처럼 우리는 정규화^{regularization}를 도입하여 모델의 오버피팅을 최대한 지연시키고 일반화 성능을 향상시킬 수 있음을 확인하였습니다. 이 과정에서 정규화 계층을 간편하게 모델에 삽입하기 위하여, nn.Module을 상속받은 클래스를 통해 서브 모듈을 정의하여 nn.Sequential에 반복하여 사용하였습니다. 이제 다음 챕터에서는 이제까지 배운 내용들을 총동원하여 MNIST 분류를 좀 더 제대로 구현하는 방법을 살펴보도록 하겠습니다.