드랍아웃

앞서 데이터 증강^{data augmentation} 기법은 데이터에 노이즈를 추가함으로써, 불필요한 특징^feature들을 모델이 학습하는 것을 방지하고자 하였는데요. 이것은 신경망의 입력 또는 출력 위치에 노이즈를 추가하는 것으로 볼 수도 있습니다. 그렇다면 만약 신경망의 중간에 노이즈를 추가 할 수는 없을까요?

드랍아웃의 동작 방식

드랍아웃^dropout[1]이 어쩌면 그 답이 될 수 있을 것 같습니다. 드랍아웃은 임의의 노드를 일정 확률로 드랍^drop해서 학습에 참여하지 않도록 하는 방법입니다. 데이터를 신경망에 통과시키는 과정^feed-forward에서 노드가 생략되므로, 자연스럽게 역전파^{back-propgatiopn}에서도 제외됩니다. 다음 그림은 드랍아웃의 개략적인 동작 방식을 보여줍니다.

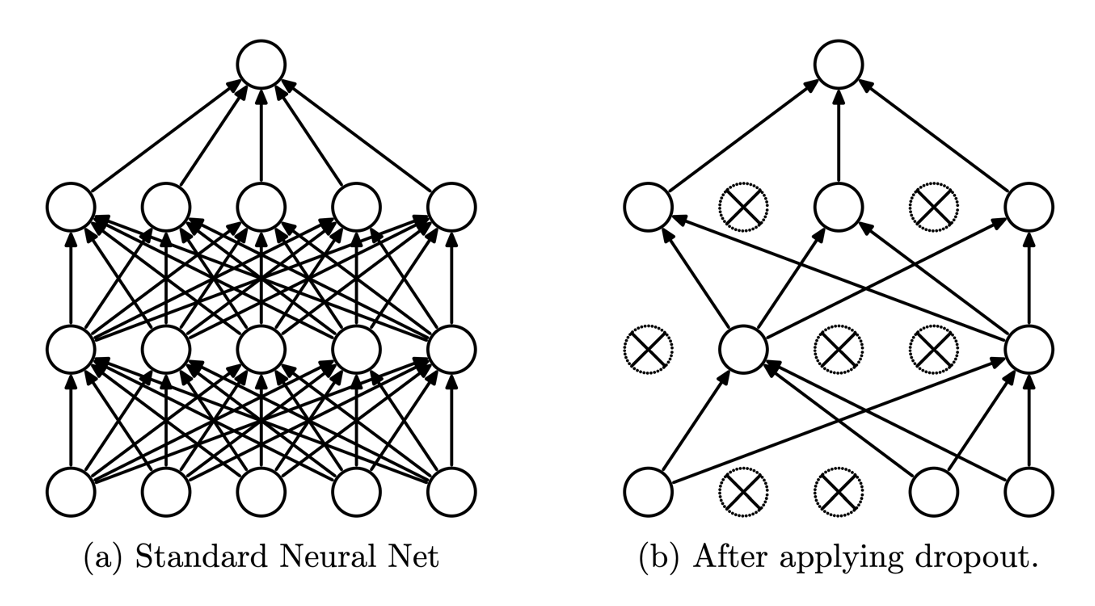
그림과 같이 일부 노드가 드랍되어, 해당 노드와 연결된 가중치들도 끊어지는 것을 볼 수 있습니다. 드랍되는 노드는 매 미니배치마다 이항분포^{binomial distribution}을 활용하여 랜덤으로 선정됩니다. 이때 노드의 드랍 확률 $p$ 가 하이퍼파라미터가 되어, 사용자가 최적의 설정 값을 찾아주어야 합니다.

[1]: Dropout: a simple way to prevent neural networks from overfitting, Srivastava et al., Journal of Machine Learning Research, 2014

학습과 추론 방식의 차이

드랍아웃에서 또 하나 특기해야 할 점은 바로 학습과 추론 방법의 차이입니다. 앞서 설명한 드랍아웃의 동작 방법은 학습에서만 적용되는 방법인데요. 추론^inference에서는 드랍되는 노드 없이 모든 노드가 항상 추론에 참여합니다.

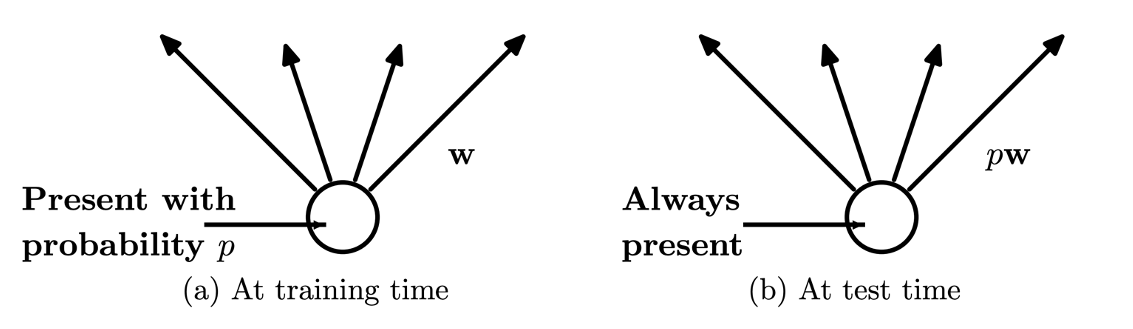
이때 추론할 때 중요한 점은 가중치 파라미터 $W$ 에 $(1-p)$ 를 곱해주어야 한다는 것입니다.^[2] 예를 들어 앞서 그림과 같이 하나의 출력 노드가 3개인 선형 계층^{linear layer}이 있다고 가정하겠습니다. 그런데 만약 $p=0.33$ 의 확률로 출력 노드에 드랍아웃이 적용되었다면, 학습할 때에는 평균적으로 2개의 노드만 살아남을 것입니다. 따라서 학습시에는 다음 계층은 평균적으로 3개 중에서 2개 노드로부터 값을 전달 받을 것입니다. 하지만 추론시에는 다음 계층은 항상 전체 노드로부터 값을 전달 받을 것입니다. 즉, 추론시에 다음 계층은 평균적으로 학습시보다 1.5배 큰 입력 값을 전달 받을 것입니다. 그러므로 추론시에는 가중치 파라미터에 $(1-p)=0.67$ 을 곱해주어 이것을 상쇄해야 합니다.

파이토치에서는 조금 다르게 구현되어 있는데요. 학습시에 $\frac{1}{1-p}$ 를 드랍아웃 계층 출력 값에 곱해주도록 합니다. 그럼 앞서 예제의 설정 값에 따르면, $\frac{1}{1-p}\approx1.5$ 를 학습시에 출력 값에 곱해주어 학습과 추론 사이의 차이를 없애도록 할 수 있습니다.

[2]: 그림에서는 출현 확률 $p$ 로 표현되어 있습니다.

드랍아웃의 구현

드랍아웃은 이전까지 소개한 정규화 기법과 달리 신경망의 계층으로 구현될 수 있습니다. 파이토치에서는 미리 구현된 드랍아웃 계층을 제공하는데요. 우리는 이것을 활용하여 쉽게 드랍아웃을 구현할 수 있습니다. 보통 드랍아웃이 구현되는 위치는 다음 그림과 같이 활성 함수^{activation function}와 다음 계층^layer 사이가 됩니다.

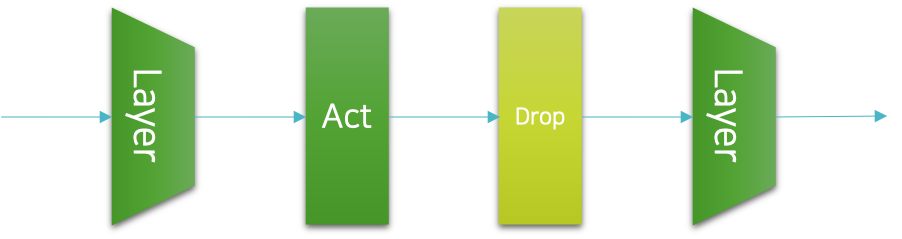
이 그림에서는 이전 계층과 활성 함수 다음에 드랍아웃이 삽입되고, 이후에 다음 계층이 존재하는 것을 확인할 수 있습니다. 이를 코드로 적용하면 다음과 같이 될 것입니다. 참고로 보통은 신경망의 양 끝단인 입력 계층 이전과 출력 계층 이후에는 드랍아웃이 적용되지 않습니다.

p = 0.3

net = nn.Sequential(
    nn.Linear(300, 200),
    nn.LeakyReLU(),
    nn.Dropout(p),
    nn.Linear(200, 100),
    nn.LeakyReLU(),
    nn.Dropout(p),
    nn.Linear(100, 50),
    nn.LeakyReLU(),
    nn.Dropout(p),
    nn.Linear(50, 10)
)

또한 추론과 학습이 다르게 동작하도록 해야 하기 때문에 학습과 추론 코드 상에서 추가적인 구현이 필요합니다. 파이토치의 nn.Module 을 상속받은 클래스는 train() 과 eval() 이라는 메서드를 제공하여 모델의 학습 모드와 추론 모드를 쉽게 왔다갔다 할 수 있도록 합니다. train() 과 eval() 이 호출되면 해당 객체 안에 포함된 드랍아웃과 같이 학습과 추론에서 다르게 동작하는 계층들은 자동으로 학습 모드와 추론 모드로 전환됩니다. 물론 드랍아웃 자체도 nn.Module 을 상속받은 클래스의 객체일테니, train() 과 eval() 을 통해 모드를 직접 전환할 수 있습니다.

for epoch_idx in range(n_epochs):
    net.train()
    for iter_idx in range(n_train_iters):
        # Training procedure

    net.eval()
    for iter_idx in range(n_valid_iters):
        # Validation procedure

따라서 학습^training과 검증^validation으로 구성되는 에포크^epoch는 내부에서 모델의 학습 모드와 추론 모드의 전환 과정이 포함되어 있어야 합니다. 모델의 기본 모드는 학습 모드이기 때문에, 만약 테스트와 같은 추론을 수행할 때 추론 모드로의 전환을 깜빡한다면 모델의 성능이 실제 성능이 비해서 낮게 나올 것입니다. 그러므로 적절한 위치에서 train() 과 eval() 의 호출을 해주는 것을 잊지 않도록 해야 합니다. 이것은 이후에 소개할 다른 정규화 기법을 포함한 대부분의 정규화 기법에서 마찬가지이기 때문에, 지금 당장의 정규화 여부와 상관 없이 기본적으로 모드 변환 코드를 항상 집어넣는 것을 권장합니다.

드랍아웃의 의미와 한계

앞서 드랍아웃을 처음 소개할 때, 드랍아웃은 신경망의 중간에 노이즈를 추가하는 기법으로 볼 수 있다고 하였습니다. 다시 생각해보면, 드랍아웃은 임의의 노드를 학습에서 생략하는 과정을 통해 특정 노드 사이의 관계가 불필요하게 강해지는 것을 방지하며, 앞서 다른 정규화 방식과 마찬가지로 학습을 방해하는 방식으로 동작하는 것임을 알 수 있습니다.

따라서 드랍아웃이 적용되면 비록 일반화 성능이 개선될 수는 있어도 손실 값의 수렴^convergence 속도가 저하될 수 있고 학습 오차^{training error}가 증가될 수 있습니다. 또한 노드의 드랍 확률 값 $p$ 가 하이퍼파라미터^{hyper-parameter}가 추가됨으로써, 사용자의 추가적인 튜닝을 요구하게 됩니다. 다행히 보통은 해당 하이퍼파라미터를 0.1 에서 0.5 사이의 값으로 0.1 단위로 튜닝하므로 많은 실험이 필요하진 않습니다.