실습: Deep Classification
이번 실습에서는 드디어 MNIST 데이터셋 분류를 해보고자 합니다. MNIST 데이터셋[1]은 한 샘플당 한 개의 0에서부터 9까지의 손 글씨 숫자로 구성되어 있습니다. 따라서 우리는 딥러닝을 통해 각 샘플이 0에서부터 9 사이에 어떤 클래스에 속하는지 분류해야 합니다.

MNIST 데이터셋은 사실 딥러닝계의 Hello World나 마찬가지인데요. 보통은 딥러닝을 접할 때 가장 먼저 접해보는 데이터셋 중에 하나입니다.[2] 하지만 우리 책에서는 이제서야 이 MNIST 데이터셋을 다루게 되는데요. 단순히 Hello World에 그치는 것이 아니라, 그동안 딥러닝의 기초를 탄탄히 배워온 만큼, MNIST 분류 문제도 여러 챕터에 걸쳐서 제대로 다뤄보고자 합니다.
[1]: https://ko.wikipedia.org/wiki/MNIST_데이터베이스
[2]: 사실 딥러닝에 와서야 굉장히 쉬운 문제로 전락했지만, 절대 만만한 문제가 아니었습니다.
데이터 준비
데이터 로딩과 학습에 필요한 라이브러리와 패키지들을 불러옵니다.
import numpy as np
from copy import deepcopy
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
파이토치 비전torchvision에서 제공하는 datasets 패키지에서 MNIST 데이터셋을 불러옵니다. 훌륭하게도 datasets 패키지는 MNIST 데이터셋이 경로에 없다면 자동으로 다운로드 받아 “../data” 경로에 저장합니다. MNIST 데이터셋은 테스트셋은 따로 제공하기때문에, train 인자를 통해서 학습과 테스트 데이터셋을 각각 불러옵니다. 이후에 이 학습 데이터셋은 다시 학습 데이터셋과 검증 데이터셋을 나뉘게 됩니다.
train = datasets.MNIST(
'../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
]),
)
test = datasets.MNIST(
'../data', train=False,
transform=transforms.Compose([
transforms.ToTensor(),
]),
)
데이터 샘플을 시각화할 수 있는 함수를 미리 하나 만들어보려합니다. 지금이야 MNIST라는 유명한 데이터셋을 다루기 때문에 딱히 데이터에 대한 분석 없이 넘어가지만, 만약 처음보는 데이터셋이라면 다양한 시각화를 통해 데이터셋에 대한 특성을 먼저 파악해야 할 것입니다.
def plot(x):
img = (np.array(x.detach().cpu(), dtype='float')).reshape(28, 28)
plt.imshow(img, cmap='gray')
plt.show()
앞서 만든 plot 함수에 학습 데이터셋의 첫 번째 샘플을 집어넣어보겠습니다.
plot(train.data[0])

MNIST 샘플의 각 픽셀은 0에서부터 255까지의 숫자로 이루어진 그레이스케일gray scale로 구성되어 있습니다. 따라서 255로 각 픽셀 값을 나눠주면, 0에서 1까지의 값으로 정규화normalization할 수 있습니다. 그리고 현재 우리의 신경망은 선형 계층으로만 이루어질 것이기 때문에, 2D 이미지도 1차원 벡터로 flatten하여 나타내야 합니다. 하나의 샘플은 $28\times28$ 크기의 픽셀들로 이루어져 있습니다.[3] 따라서 이 2차원 행렬을 1차원 벡터로 flatten할 경우, 784 크기의 벡터가 될 것입니다.
x = train.data.float() / 255.
y = train.targets
x = x.view(x.size(0), -1)
print(x.shape, y.shape)
다음의 프린트 결과와 같이 MNIST는 60,000개의 학습 데이터셋 샘플을 가지고 있습니다.
torch.Size([60000, 784]) torch.Size([60000])
앞서와 마찬가지로, 우리는 항상 하드코딩hard-coding[4]을 최소화 해야 합니다. 따라서 어떠한 크기의 흑백 이미지가 들어오더라도 동작하는 코드를 만들어보겠습니다. 이를 위해서 딥러닝 모델의 입력과 출력의 크기를 자동으로 계산하도록 합니다.
input_size = x.size(-1)
output_size = int(max(y)) + 1
print('input_size: %d, output_size: %d' % (input_size, output_size))
데이터셋의 차원의 크기를 활용하여 모델 입력 크기를 알아내고, 최대 클래스 인덱스를 알아내어 모델 출력의 크기를 알아냅니다. 그 결과, 모델은 784 크기의 입력을 받아, 10 개의 확률 값을 뱉어낼 것입니다.
input_size: 784, output_size: 10
앞서 말했듯이, MNIST는 테스트 데이터셋을 따로 제공하므로, 학습 데이터와 검증 데이터를 나누는 작업만 수행하면 됩니다. 따라서 이번에는 8:2의 비율로 학습/검증 데이터셋을 나누도록 하겠습니다.
# Train / Valid ratio
ratios = [.8, .2]
train_cnt = int(x.size(0) * ratios[0])
valid_cnt = int(x.size(0) * ratios[1])
test_cnt = len(test.data)
cnts = [train_cnt, valid_cnt]
print("Train %d / Valid %d / Test %d samples." % (train_cnt, valid_cnt, test_cnt))
indices = torch.randperm(x.size(0))
x = torch.index_select(x, dim=0, index=indices)
y = torch.index_select(y, dim=0, index=indices)
x = list(x.split(cnts, dim=0))
y = list(y.split(cnts, dim=0))
x += [(test.data.float() / 255.).view(test_cnt, -1)]
y += [test.targets]
for x_i, y_i in zip(x, y):
print(x_i.size(), y_i.size())
60,000개의 학습 데이터 샘플들이 각각 48,000개와 12,000개로 학습/검증 데이터로 다시 나뉘어졌습니다.
Train 48000 / Valid 12000 / Test 10000 samples.
torch.Size([48000, 784]) torch.Size([48000])
torch.Size([12000, 784]) torch.Size([12000])
torch.Size([10000, 784]) torch.Size([10000])
[3]: 여기서 만약에 컬러 이미지라면 RGB 각 색깔을 나타내야 하기 때문에, $28\times28\times3$ 크기가 되어야 할 것입니다.
[4]: 소스코드에 직접 특정 상수 값을 적어 넣는 것을 의미합니다. 하드코딩이 많아지면 추후 코드 유지/보수 측면에서 굉장히 큰 부담이 됩니다.
학습 코드 구현
이번에도 nn.Sequential을 활용하여 MNIST 이미지를 분류하기 위한 모델을 구현해봅니다. 한 개의 MNIST 이미지는 변환을 통해 784개의 요소를 갖는 1차원 벡터가 될 것입니다. 그리고 우리의 모델은 784차원 벡터를 입력을 받아, 10개 클래스에 속할 확률 값을 각각 출력해야 합니다. 즉, 입력의 크기는 784, 출력의 크기는 10이 됩니다. 앞서의 문제들보다 입력 크기가 더 큰 것을 볼 수 있습니다. 다시말해 MNIST는 훨씬 더 큰 공간인 784차원에 정의되어 있는 데이터셋으로 볼 수 있으며, 해당 공간의 대부분은 샘플이 존재하지 않는 비어있는 공간이기 때문에 희소한 데이터라고 말할 수 있습니다. 그러므로 이전까지의 문제들보다 더 어려운 문제라고 볼 수 있으며, 우리는 딥러닝 모델의 용량capacity을 늘려 문제 해결 능력을 향상시켜야 할 것입니다. 따라서 모델의 크기를 충분히 깊고 넓게 가져가도록 하겠습니다.
model = nn.Sequential(
nn.Linear(input_size, 500),
nn.LeakyReLU(),
nn.Linear(500, 400),
nn.LeakyReLU(),
nn.Linear(400, 300),
nn.LeakyReLU(),
nn.Linear(300, 200),
nn.LeakyReLU(),
nn.Linear(200, 100),
nn.LeakyReLU(),
nn.Linear(100, 50),
nn.LeakyReLU(),
nn.Linear(50, output_size),
nn.LogSoftmax(dim=-1),
)
이렇게 선언한 모델의 가중치 파라미터를 아담Adam 옵티마이저에 등록하고, NLLNegative Log-likelihood 손실 함수도 선언합니다. NLL 손실 함수를 사용하기 위해서 로그소프트맥스Log softmax 함수를 모델의 마지막에 사용한 것에 주목하세요.
optimizer = optim.Adam(model.parameters())
crit = nn.NLLLoss()
이제까지는 작은 데이터셋과 작은 모델 위주로 실습을 진행하였기 때문에, CPU에서 학습을 진행하였더라도 큰 불편함이 없었습니다. 이번에는 6만장의 이미지 데이터를 조금 더 큰 모델에서 학습 할 것이므로 가능하다면 GPU에서 학습을 진행해보도록 합니다. 물론 아직 실무에서의 작업량에 비해서는 매우 작은 데이터셋과 작은 모델이므로 CPU에서 학습을 진행해도 무방합니다. 다음의 코드는 만약 CUDA가 활용 가능하다면, GPU를 기본 디바이스로 지정하는 코드입니다.
device = torch.device('cpu')
if torch.cuda.is_available():
device = torch.device('cuda')
이렇게 지정된 device 변수를 to함수나 cuda함수에 넣어주면, 텐서나 모델을 GPU로 옮기거나 복사할 수 있게 됩니다. 다음 코드에서는 모델의 to 함수에 device를 지정해주어 원하는 디바이스로 모델을 이동하고, 학습/검증/테스트 데이터셋에 대해서도 복사를 진행하는 내용이 구현되어 있습니다. 똑같은 to 함수이더라도 모델은 이동이고, 텐서를 복사로 적용된다는 점에 유의하세요. 또한 GPU가 없어서 device 변수가 CPU로 적용되어 있다면, 해당 코드가 실행되더라도 아무 작업도 수행되지 않습니다.
model = model.to(device)
x = [x_i.to(device) for x_i in x]
y = [y_i.to(device) for y_i in y]
다음은 학습에 필요한 하이퍼 파라미터 및 변수들을 초기화 해줍니다.
n_epochs = 1000
batch_size = 256
print_interval = 10
lowest_loss = np.inf
best_model = None
early_stop = 50
lowest_epoch = np.inf
다음의 학습 코드는 앞서의 실습과 완전 똑같은 코드입니다. n_epochs 만큼의 에포크를 반복하는 for 반복문 내부에는 학습과 검증을 위한 for 반복문이 각각 존재하며, 학습에 앞서 학습 데이터를 임의의 순서로 섞어주는 코드가 구현되어 있습니다. 학습에서는 피드포워드feed-forward, 역전파back-propagation, 경사하강gradient descent이 진행됩니다. 검증에서는 피드포워드만 진행됩니다. 그리고 학습/검증의 두 for 반복문이 끝나면, 최저 검증 손실 값과 현재 검증 손실 값을 비교하여 모델을 저장하는 로직이 구현되어 있습니다.
train_history, valid_history = [], []
for i in range(n_epochs):
indices = torch.randperm(x[0].size(0)).to(device)
x_ = torch.index_select(x[0], dim=0, index=indices)
y_ = torch.index_select(y[0], dim=0, index=indices)
x_ = x_.split(batch_size, dim=0)
y_ = y_.split(batch_size, dim=0)
train_loss, valid_loss = 0, 0
y_hat = []
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = crit(y_hat_i, y_i.squeeze())
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += float(loss)
train_loss = train_loss / len(x_)
with torch.no_grad():
x_ = x[1].split(batch_size, dim=0)
y_ = y[1].split(batch_size, dim=0)
valid_loss = 0
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = crit(y_hat_i, y_i.squeeze())
valid_loss += float(loss)
y_hat += [y_hat_i]
valid_loss = valid_loss / len(x_)
train_history += [train_loss]
valid_history += [valid_loss]
if (i + 1) % print_interval == 0:
print('Epoch %d: train loss=%.4e valid_loss=%.4e lowest_loss=%.4e' % (
i + 1,
train_loss,
valid_loss,
lowest_loss,
))
if valid_loss <= lowest_loss:
lowest_loss = valid_loss
lowest_epoch = i
best_model = deepcopy(model.state_dict())
else:
if early_stop > 0 and lowest_epoch + early_stop < i + 1:
print("There is no improvement during last %d epochs." % early_stop)
break
print("The best validation loss from epoch %d: %.4e" % (lowest_epoch + 1, lowest_loss))
model.load_state_dict(best_model)
이렇게 구현한 코드를 통해 학습을 수행하면 다음과 같이 손실 값이 출력됩니다.
Epoch 10: train loss=2.2119e-02 valid_loss=1.1302e-01 lowest_loss=9.5662e-02
Epoch 20: train loss=1.1494e-02 valid_loss=1.1124e-01 lowest_loss=9.5662e-02
Epoch 30: train loss=7.9660e-03 valid_loss=1.1719e-01 lowest_loss=9.5662e-02
Epoch 40: train loss=4.3731e-03 valid_loss=1.2816e-01 lowest_loss=9.5662e-02
Epoch 50: train loss=4.4661e-03 valid_loss=1.3524e-01 lowest_loss=9.5662e-02
There is no improvement during last 50 epochs.
The best validation loss from epoch 8: 9.5662e-02
일찌감치 8번째 에포크에서 최저 검증 손실 값이 달성된 것을 볼 수 있습니다. 그 이후에는 학습 데이터에 대한 손실 값은 계속 내려가고 있지만, 검증 손실 값이 점차 높아지는 것을 보아, 완전히 오버피팅 단계에 접어들었음을 알 수 있습니다.
손실 곡선 확인
이번에도 앞서 보았던 손실 값의 변화를 직접 화면에 그려보도록 하겠습니다. train_history와 valid_history에 저장된 각 에포크별 손실 값들을 그려주도록 합니다.
plot_from = 0
plt.figure(figsize=(20, 10))
plt.grid(True)
plt.title("Train / Valid Loss History")
plt.plot(
range(plot_from, len(train_history)), train_history[plot_from:],
range(plot_from, len(valid_history)), valid_history[plot_from:],
)
plt.yscale('log')
plt.show()
앞서 보았던 대로 학습 초반에 제일 낮은 검증 손실 값을 찍은 후에, 점차 천천히 검증 손실 값이 올라가는 것을 보여줍니다. 그리고 학습 손실 값은 재미있게도 후반부에 좀 더 급격하게 떨어지는 모습을 보여줍니다.

결과 확인
이번에는 검증 손실 값을 통해 선정된 베스트 모델을 활용하여 테스트 데이터셋에 대해 성능을 측정해보도록 하겠습니다. 앞서 말했듯이, MNIST 데이터셋은 테스트 데이터셋은 10,000장의 이미지 샘플이 따로 지정되어 있습니다. 따라서 임의로 나눈 학습/검증/테스트 데이터셋에 비해 좀 더 객관적으로 테스트 데이터셋에 대한 성능을 측정할 수 있습니다. 아래의 코드는 앞서 실습에서와 똑같은 코드입니다.
test_loss = 0
y_hat = []
with torch.no_grad():
x_ = x[-1].split(batch_size, dim=0)
y_ = y[-1].split(batch_size, dim=0)
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = crit(y_hat_i, y_i.squeeze())
test_loss += loss
y_hat += [y_hat_i]
test_loss = test_loss / len(x_)
y_hat = torch.cat(y_hat, dim=0)
print("Test loss: %.4e" % test_loss)
테스트 손실은 검증 손실 값보다 약간 더 작은 값이 나오는 것을 확인할 수 있습니다. 어쨌든 오차 범위 내의 비슷한 값이라고 볼 수 있으므로, 정상적인 상황이라고 볼 수 있습니다. 만약 검증 손실 값과 테스트 손실 값이 오차 범위 밖의 차이를 보여준다면, 뭔가 잘못된 상황이라고 볼 수 있겠지요.
Test loss: 8.9894e-02
그럼 좀 더 명확하게 성능을 파악하기 위해서, 테스트 데이터셋에 대해 정확도를 측정해보도록 하겠습니다. 우리는 분류 문제를 다루고 있으므로, 신경망의 마지막 계층은 확률값 또는 로그 확률값을 나타내고 있을 것입니다. 따라서 마지막 계층의 출력값 중에서 가장 높은 값을 가지고 있는 클래스 인덱스가 모델이 예측한 클래스의 인덱스라고 볼 수 있습니다. 이는 파이토치의 argmax 함수를 통해 구현할 수 있습니다.
argmax를 통해 구한 예측 클래스 인덱스가 실제 정답 클래스 인덱스와 같은 경우를 모두 더하면, 테스트 데이터셋에서 예측이 맞은 횟수를 구할 수 있을 것입니다. 그럼 전체 테스트셋의 갯수로 맞은 횟수를 나누어주어 정확도를 계산할 수 있습니다.
correct_cnt = (y[-1].squeeze() == torch.argmax(y_hat, dim=-1)).sum()
total_cnt = float(y[-1].size(0))
print("Test Accuracy: %.4f" % (correct_cnt / total_cnt))
정확도를 계산해보니 무려 97.57%의 정확도를 보여줍니다. 딱히 튜닝을 한 부분이 없는데도 불구하고 매우 높은 정확도를 보여주네요.
Test Accuracy: 0.9757
이번에는 혼동 행렬confusion matrix을 출력하기 위해 필요한 패키지들을 불러옵니다.
import pandas as pd
from sklearn.metrics import confusion_matrix
sklearn에서 제공하는 confusion_matrix 함수를 통해 우리는 쉽게 혼동 행렬을 계산할 수 있습니다. confusion_matrix 함수의 결과물을 받아 화면에 이쁘게 찍어주기 위해서 판다스Pandas 데이터프레임에 넣어줍니다.
pd.DataFrame(confusion_matrix(y[-1], torch.argmax(y_hat, dim=-1)),
index=['true_%d' % i for i in range(10)],
columns=['pred_%d' % i for i in range(10)])
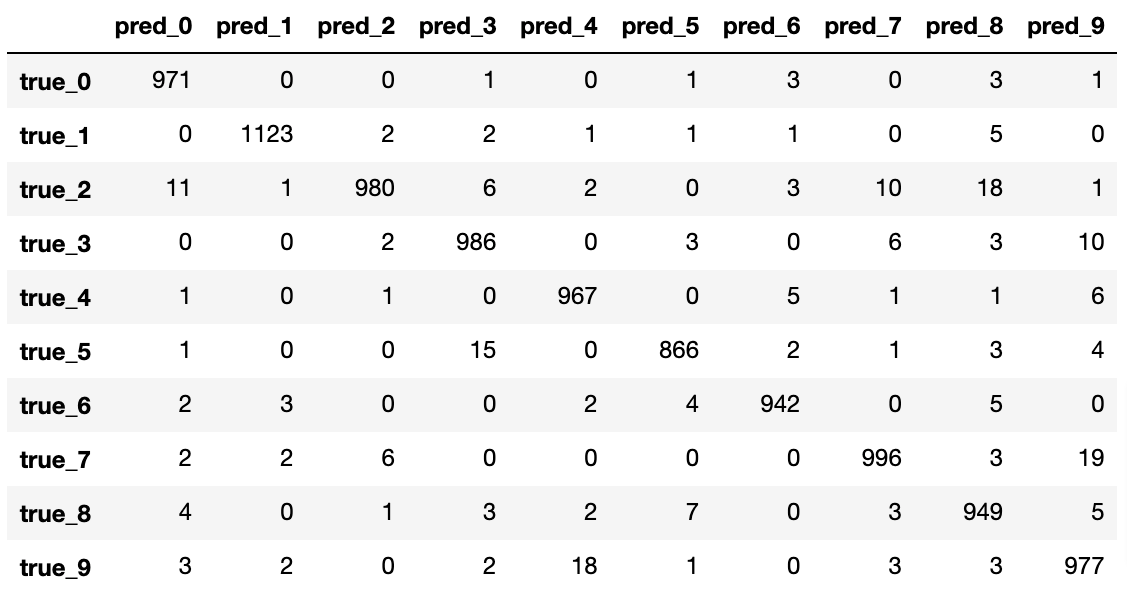
결과를 해석해보면 당연히 대부분의 문제들에 대해서는 정답을 맞추었기 때문에 행렬의 대각 성분의 값이 높은 것을 확인할 수 있습니다. 그리고 대각 성분 이외에서 높은 부분들을 확인하면 현재 모델이 약한 부분을 확인할 수 있을텐데요. 우리의 모델은 2를 8이라고 예측하거나, 7을 9라고 예측하거나, 9를 4라고 예측하는 경우가 많음을 확인할 수 있습니다. 재미있는 것은 헷갈림이 방향성을 지니고 있다는 것이네요. 예를 들어, 7을 9라고 헷갈리는 경우는 많지만, 9를 7이라고 헷갈리는 경우는 많지 않는 것을 확인할 수 있습니다. 만약 우리가 실무를 수행하고 있다면, 이처럼 약한 부분을 파악하고, 데이터를 보강하거나 모델을 보강하는 형태로 나아가야 할 것입니다.