실습: Deep Binary Classification
데이터 준비
앞서 로지스틱 회귀logistic regression에서 실습했던 유방암 예측 데이터셋을 활용하여 딥러닝을 통한 이진 분류를 실습하도록 합니다. 다음과 같이 필요한 라이브러리들을 불러옵니다.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from copy import deepcopy
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_breast_cancer
유방암 데이터셋을 판다스Pandas 데이터프레임에 넣고, class 열에 정답 데이터를 넣어줍니다.
cancer = load_breast_cancer()
df = pd.DataFrame(cancer.data, columns=cancer.feature_names)
df['class'] = cancer.target
앞서 로지스틱 회귀에서 데이터셋에 대한 분석은 어느정도 진행하였으니, 바로 데이터셋 분할에 나서도록 하겠습니다. 이를 위해서 파이토치에서 필요한 패키지들을 불러옵니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
데이터프레임의 넘파이Numpy 데이터를 파이토치 데이터로 변환하고 크기를 확인합니다.
data = torch.from_numpy(df.values).float()
x = data[:, :-1]
y = data[:, -1:]
print(x.shape, y.shape)
유방암 데이터는 569개의 입출력 쌍으로 샘플이 구성되어 있습니다. 입력 데이터는 한 샘플이 569 차원의 벡터로 구성되며, 출력 데이터 샘플은 하나의 이진 값으로 표현됩니다.
torch.Size([569, 30]) torch.Size([569, 1])
이제 이 데이터를 6:2:2의 비율로 학습/검증/테스트 데이터셋으로 나눠보겠습니다. 앞서 챕터의 실습과 똑같은 코드입니다.
# Train / Valid / Test ratio
ratios = [.6, .2, .2]
train_cnt = int(data.size(0) * ratios[0])
valid_cnt = int(data.size(0) * ratios[1])
test_cnt = data.size(0) - train_cnt - valid_cnt
cnts = [train_cnt, valid_cnt, test_cnt]
print("Train %d / Valid %d / Test %d samples." % (train_cnt, valid_cnt, test_cnt))
6:2:2의 비율로 나눌 경우, 각각 341개, 113개, 115개의 샘플로 학습/검증/테스트 데이터셋이 구성됩니다.
Train 341 / Valid 113 / Test 115 samples.
이제 이 갯수대로 랜덤하게 섞어 나누어줍니다.
indices = torch.randperm(data.size(0))
x = torch.index_select(x, dim=0, index=indices)
y = torch.index_select(y, dim=0, index=indices)
x = x.split(cnts, dim=0)
y = y.split(cnts, dim=0)
for x_i, y_i in zip(x, y):
print(x_i.size(), y_i.size())
나뉜 크기를 확인해봅니다.
torch.Size([341, 30]) torch.Size([341, 1])
torch.Size([113, 30]) torch.Size([113, 1])
torch.Size([115, 30]) torch.Size([115, 1])
그리고 학습 데이터를 기준으로 표준 스케일러를 학습한 후, 해당 스케일러를 학습/검증/테스트 데이터셋에 똑같이 적용합니다.
scaler = StandardScaler()
scaler.fit(x[0].numpy())
x = [torch.from_numpy(scaler.transform(x[0].numpy())).float(),
torch.from_numpy(scaler.transform(x[1].numpy())).float(),
torch.from_numpy(scaler.transform(x[2].numpy())).float()]
학습 코드 구현
nn.Sequential 클래스를 활용하여 모델을 구현합니다. 선형 계층과 리키 렐루를 차례로 집어넣어줍니다.[1] 이어지는 계층의 입력 크기가 이전 계층의 출력 크기와 맞도록 해줘야 함을 참고하세요. 모델 구조의 마지막에는 시그모이드를 넣어주어 이진 분류를 위한 준비를 마칩니다. 그리고 아담 옵티마이저에 선언한 모델 가중치 파라미터를 등록해줍니다.
model = nn.Sequential(
nn.Linear(x[0].size(-1), 25),
nn.LeakyReLU(),
nn.Linear(25, 20),
nn.LeakyReLU(),
nn.Linear(20, 15),
nn.LeakyReLU(),
nn.Linear(15, 10),
nn.LeakyReLU(),
nn.Linear(10, 5),
nn.LeakyReLU(),
nn.Linear(5, y[0].size(-1)),
nn.Sigmoid(),
)
optimizer = optim.Adam(model.parameters())
다음은 학습에 필요한 하이퍼파라미터를 설정해줍니다. 어차피 조기 종료를 걸어두었으니, n_epochs 파라미터를 굉장히 크게 잡아보았습니다.
n_epochs = 10000
batch_size = 32
print_interval = 10
early_stop = 100
lowest_loss = np.inf
best_model = None
lowest_epoch = np.inf
다음은 모델 학습 이터레이션을 진행하는 반복문 코드입니다. 여기서 눈여겨 보아야 할 부분은 손실 함수를 BCE 함수로 쓴다는 점이고, 이는 F.binary_cross_entropy를 활용하는 것을 볼 수 있습니다. 나머지는 앞서 챕터에서 실습한 코드와 거의 똑같기 때문에 자세한 설명은 생략하도록 하겠습니다. 설명이 필요하신 독자분들은 앞 챕터들을 참고 바랍니다. 이처럼 한번 만든 학습 코드는 제대로 만든다면 계속 재활용해서 쓸 수 있게 됩니다.
train_history, valid_history = [], []
for i in range(n_epochs):
indices = torch.randperm(x[0].size(0))
x_ = torch.index_select(x[0], dim=0, index=indices)
y_ = torch.index_select(y[0], dim=0, index=indices)
x_ = x_.split(batch_size, dim=0)
y_ = y_.split(batch_size, dim=0)
train_loss, valid_loss = 0, 0
y_hat = []
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = F.binary_cross_entropy(y_hat_i, y_i)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += float(loss)
train_loss = train_loss / len(x_)
with torch.no_grad():
x_ = x[1].split(batch_size, dim=0)
y_ = y[1].split(batch_size, dim=0)
valid_loss = 0
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = F.binary_cross_entropy(y_hat_i, y_i)
valid_loss += float(loss)
y_hat += [y_hat_i]
valid_loss = valid_loss / len(x_)
train_history += [train_loss]
valid_history += [valid_loss]
if (i + 1) % print_interval == 0:
print('Epoch %d: train loss=%.4e valid_loss=%.4e lowest_loss=%.4e' % (
i + 1,
train_loss,
valid_loss,
lowest_loss,
))
if valid_loss <= lowest_loss:
lowest_loss = valid_loss
lowest_epoch = i
best_model = deepcopy(model.state_dict())
else:
if early_stop > 0 and lowest_epoch + early_stop < i + 1:
print("There is no improvement during last %d epochs." % early_stop)
break
print("The best validation loss from epoch %d: %.4e" % (lowest_epoch + 1, lowest_loss))
model.load_state_dict(best_model)
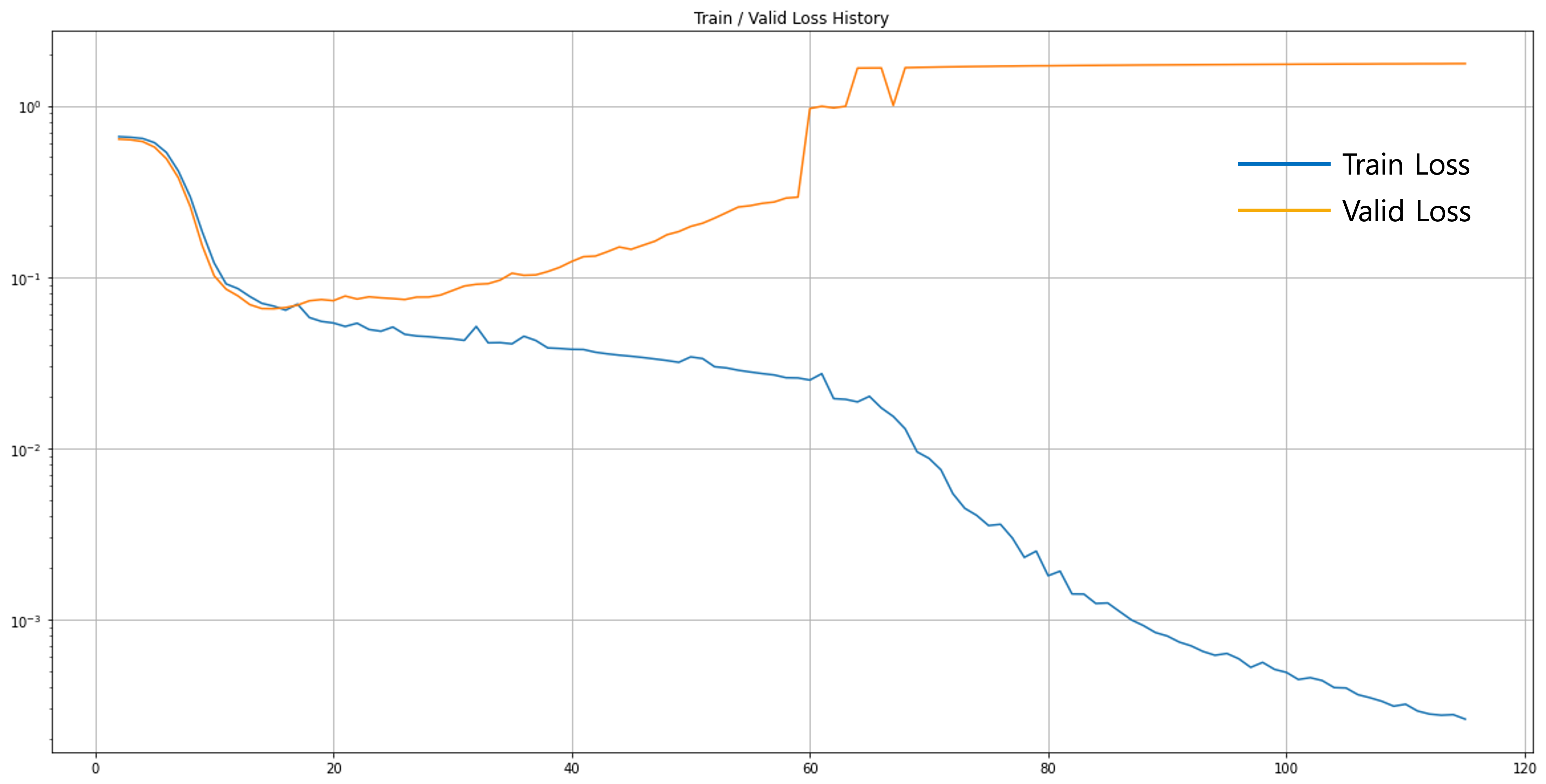
학습을 실행하면 다음과 같이 10 에포크마다 손실 값을 프린트하는 것을 확인할 수 있습니다. 재미있게도 워낙 데이터가 작고 단순하기 때문인지 16번째 에포크에서 최소 손실 값을 기록한 것을 확인할 수 있습니다. 이후에는 확연한 오버피팅이 시작되어 학습 손실 값은 계속해서 작아지는데 반해, 검증 손실 값이 계속해서 올라가버리는 것을 볼 수 있습니다.
Epoch 10: train loss=1.8343e-01 valid_loss=1.5224e-01 lowest_loss=2.5708e-01
Epoch 20: train loss=5.4922e-02 valid_loss=7.3675e-02 lowest_loss=6.5090e-02
Epoch 30: train loss=4.4038e-02 valid_loss=7.8259e-02 lowest_loss=6.5090e-02
Epoch 40: train loss=3.8160e-02 valid_loss=1.1363e-01 lowest_loss=6.5090e-02
Epoch 50: train loss=3.1684e-02 valid_loss=1.8388e-01 lowest_loss=6.5090e-02
Epoch 60: train loss=2.5677e-02 valid_loss=2.9206e-01 lowest_loss=6.5090e-02
Epoch 70: train loss=9.5019e-03 valid_loss=1.6712e+00 lowest_loss=6.5090e-02
Epoch 80: train loss=2.5008e-03 valid_loss=1.7079e+00 lowest_loss=6.5090e-02
Epoch 90: train loss=8.3700e-04 valid_loss=1.7277e+00 lowest_loss=6.5090e-02
Epoch 100: train loss=5.0989e-04 valid_loss=1.7420e+00 lowest_loss=6.5090e-02
Epoch 110: train loss=3.1076e-04 valid_loss=1.7533e+00 lowest_loss=6.5090e-02
There is no improvement during last 100 epochs.
The best validation loss from epoch 16: 6.5090e-02
[1]: 사실 데이터가 적기 때문에 이렇게 깊게 쌓을 필요가 없을 수도 있습니다.
손실 곡선 확인
그래서 손실 곡선을 찍어 확인해보면 학습 초반부 함께 내려가던 손실 값이 16번째 에포크 이후로 벌어지는 것을 확인할 수 있습니다. 실제로 조기 종료 파라미터를 바꿔 학습을 더 진행해보면 학습 손실 값은 계속해서 내려가는 것을 확인할 수 있습니다.
plot_from = 2
plt.figure(figsize=(20, 10))
plt.grid(True)
plt.title("Train / Valid Loss History")
plt.plot(
range(plot_from, len(train_history)), train_history[plot_from:],
range(plot_from, len(valid_history)), valid_history[plot_from:],
)
plt.yscale('log')
plt.show()
결과 확인
앞서와 마찬가지로 같은 코드를 활용하여 테스트 데이터셋에 대해서 평균 손실 값을 구해봅니다.
test_loss = 0
y_hat = []
with torch.no_grad():
x_ = x[2].split(batch_size, dim=0)
y_ = y[2].split(batch_size, dim=0)
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = F.binary_cross_entropy(y_hat_i, y_i)
test_loss += loss # Gradient is already detached.
y_hat += [y_hat_i]
test_loss = test_loss / len(x_)
y_hat = torch.cat(y_hat, dim=0)
sorted_history = sorted(zip(train_history, valid_history),
key=lambda x: x[1])
print("Train loss: %.4e" % sorted_history[0][0])
print("Valid loss: %.4e" % sorted_history[0][1])
print("Test loss: %.4e" % test_loss)
Train loss: 6.7450e-02
Valid loss: 6.5090e-02
Test loss: 4.1954e-02
이번 실습은 일반적인 회귀regression가 아닌 분류 실습이기 때문에, 정확도accruracy도 계산할 수 있습니다. 모델의 예측 값이 0.5보다 클 경우에는 1로 예측한 것으로 가정하고, 작거나 같은 경우에는 0으로 예측한 것이라고 가정합니다. 그렇게 가정했을 때, 실제 정답과 똑같은 갯수를 구하고 전체 갯수로 나누면 정확도를 구할 수 있습니다.
correct_cnt = (y[2] == (y_hat > .5)).sum()
total_cnt = float(y[2].size(0))
print('Test Accuracy: %.4f' % (correct_cnt / total_cnt))
계산 결과 테스트 데이터셋에 대해서 무려 98%의 높은 정확도를 보이는 것으로 나타났습니다.
Test Accuracy: 0.9826
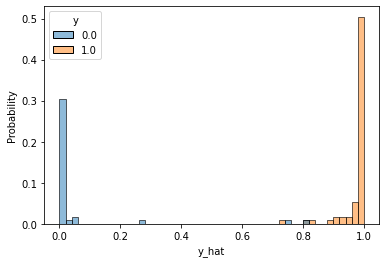
그럼 예측 값의 분포도 확인해보도록 하겠습니다. 각 클래스별로 다른 색깔로 칠해 히스토그램histogram으로 나타냈을 떄, 각 클래스의 분포가 서로 겹치지 않을수록 좋은 예측이라고 볼 수 있습니다.
df = pd.DataFrame(torch.cat([y[2], y_hat], dim=1).detach().numpy(),
columns=["y", "y_hat"])
sns.histplot(df, x='y_hat', hue='y', bins=50, stat='probability')
plt.show()
그림을 확인해보면 극히 일부를 제외하고 대부분 왼쪽과 오른쪽에 잘 나뉘어져 있는 것을 확인할 수 있습니다.
이번에는 AUROC를 구해보도록 하겠습니다. AUROC는 sklearn을 활용해서 쉽게 계산할 수 있습니다.
from sklearn.metrics import roc_auc_score
roc_auc_score(df.values[:, 0], df.values[:, 1])
정답 값과 예측 실수 값을 함께 넣어주면 자동으로 계산해주는데요, 앞서 그림에서 보았듯이 두 클래스의 분포가 확연하게 나뉠 수 있는 상황이기 때문에 매우 높은 값을 보여줍니다.
0.9990112063282794