실습: 데이터 나누기
데이터 준비
사실 이제까지 실습은 모두 잘못된 방법이었습니다. 이제까지는 학습데이터셋에 모델을 피팅fitting시키면서 학습 손실 값만 살펴보았습니다. 그리고 학습 데이터의 손실 값을 낮추고선, 모델의 성능을 확인한다고 손실 값이나 정확도accuracy를 찍어보며 잘했다고 박수쳐왔습니다. 하지만 이번 챕터를 배운 여러분은 이제 그 방법은 잘못된 것임을 잘 아실 것입니다. 이제 학습, 검증, 테스트 데이터를 잘 나누고 모델을 학습시키고, 모델이 객관적으로 잘 학습되었는지 체크하는 실습을 수행할 것입니다.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_california_housing
필요한 라이브러리 패키지들을 불러옵니다. 그리고 앞서 실습에서 활용했던 캘리포니아 하우징 데이터셋을 불러옵니다. 앞서 실습과 같이 Target 열에 우리가 예측해야하는 출력 값들을 넣어줍니다.
california = fetch_california_housing()
df = pd.DataFrame(california.data, columns=california.feature_names)
df["Target"] = california.target
본격적으로 데이터를 나누기에 앞서, 필요한 파이토치 패키지들을 불러옵니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
캘리포니아 하우징 데이터셋의 값을 파이토치 Float 텐서로 변환합니다. 그리고 입력 데이터를 x 변수에 슬라이싱하여 할당하고, 출력 데이터를 y 변수에 슬라이싱하여 할당합니다.
data = torch.from_numpy(df.values).float()
x = data[:, :-1]
y = data[:, -1:]
print(x.size(), y.size())
x와 y의 크기를 출력해보면, 20640의 샘플들로 데이터셋이 구성된 것을 확인할 수 있습니다. 입력 변수는 한 샘플당 8개의 값을 가지고 있으며, 출력 변수는 하나의 값(스칼라scalar)으로 되어 있음을 볼 수 있습니다.
torch.Size([20640, 8]) torch.Size([20640, 1])
이렇게 준비된 입출력을 이제 임의로 학습, 검증, 테스트 데이터로 나눌 차례입니다. 앞서 이론에서 배웠듯이, 60%의 학습 데이터와 20%의 검증 데이터, 20%의 테스트 데이터로 구성하기 위해서 미리 비율을 설정합니다.
# Train / Valid / Test ratio
ratios = [.6, .2, .2]
그럼 ratios에 담긴 값들을 활용하여 실제 데이터셋에서 몇 개의 샘플들이 각각 학습, 검증, 테스트셋에 할당되어야 하는지 구할 수 있습니다.
train_cnt = int(data.size(0) * ratios[0])
valid_cnt = int(data.size(0) * ratios[1])
test_cnt = data.size(0) - train_cnt - valid_cnt
cnts = [train_cnt, valid_cnt, test_cnt]
print("Train %d / Valid %d / Test %d samples." % (train_cnt, valid_cnt, test_cnt))
전체 20640개의 샘플들 중에 학습 데이터는 12384개가 되어야 하며, 검증 데이터와 테스트 데이터는 각각 4128개가 되어야 합니다.
Train 12384 / Valid 4128 / Test 4128 samples.
다시 한번 이때 중요한건 앞의 비율로 데이터셋을 나누되, 임의로 샘플들을 선정하여 나누어야 한다는 것입니다. 다음 코드를 통해서 데이터셋 랜덤 셔플링random shuffling 후, 나누기를 수행합니다. 또 주목해야 할 점은 x와 y에 대해서 각각 랜덤 선택 작업을 수행하는 것이 아닌, 쌍으로 짝지어 수행한다는 점입니다. 이것은 마치 앞서 SGD를 실습 할 때와 똑같은 상황인데요. 만약 x와 y를 각각 따로 섞어 둘의 관계가 깨져버린다면, 아무 의미 없는 노이즈로 가득찬 데이터가 될 것이기 때문입니다. 다음의 코드를 보면, 데이터셋을 나누는 코드는 사실 앞서 SGD에서 미니배치를 나누는 것과 상당히 유사한 것을 볼 수 있습니다.
# Shuffle before split.
indices = torch.randperm(data.size(0))
x = torch.index_select(x, dim=0, index=indices)
y = torch.index_select(y, dim=0, index=indices)
# Split train, valid and test set with each count.
x = list(x.split(cnts, dim=0))
y = y.split(cnts, dim=0)
for x_i, y_i in zip(x, y):
print(x_i.size(), y_i.size())
이 작업이 끝나면, 앞서 6:2:2 의 비율대로 학습, 검증, 테스트셋이 나뉜 것을 확인할 수 있습니다. 이제 학습에 들어가면 12384개의 학습 샘플들을 매 에포크epoch마다 임의로 섞어 미니배치들을 구성하여 학습 이터레이션iteration을 돌게 됩니다.
torch.Size([12384, 8]) torch.Size([12384, 1])
torch.Size([4128, 8]) torch.Size([4128, 1])
torch.Size([4128, 8]) torch.Size([4128, 1])
이처럼 데이터셋이 정상적으로 나뉜 것을 확인하면, 데이터셋 정규화normalization 작업을 마저 수행합니다. 사실 돌이켜보면, 이전 실습에서는 데이터셋을 불러오자마자 표준 스케일링을 통해 정규화를 진행했습니다. 하지만 이번 실습에서는 이제서야 정규화를 진행하고 있는데요. 왜냐하면 여기서도 데이터셋을 피팅하는 작업이 수행되기 때문입니다.
표준 스케일링의 과정을 자세히 들여다보면, 표준 스케일링을 위해서는 데이터셋의 각 열에 대해서 평균과 표준편차를 구해야 합니다. 이 과정을 통해서 데이터셋의 각 열의 분포를 추정하고, 추정된 평균과 표준편차를 활용하여 표준정규분포standard normal distribution로 변환합니다. 그러므로 만약 검증 데이터 또는 테스트 데이터를 학습 데이터와 합친 상태에서 평균과 표준편차를 추정한다면, 정답을 보는 것과 같습니다. 물론 아주 잘 정의된 매우 큰 데이터셋이라면, 임의로 학습 데이터와 검증/테스트 데이터셋을 나눌 때 그 분포가 매우 유사하겠지만, 그렇다고 해서 학습 데이터와 테스트 데이터를 합친 상태에서 평균과 표준편차를 추정해도 되는 것은 아닙니다.
따라서 다음 코드를 보면 학습데이터인 x[0] 에 대해서 표준 스케일링을 피팅fitting시키고, 이후에 해당 스케일러를 활용하여 학습(x[0]), 검증(x[1]), 테스트(x[2]) 데이터에 대해서 정규화를 진행하는 것을 볼 수 있습니다. 이처럼 학습 데이터만을 활용하여 정규화를 진행하는 것은 매우 중요하고 실수가 잦은 부분이오니, 여러분들도 주의깊게 살펴보시고 유념하시기 바랍니다.
scaler = StandardScaler()
scaler.fit(x[0].numpy()) # You must fit with train data only.
x[0] = torch.from_numpy(scaler.transform(x[0].numpy())).float()
x[1] = torch.from_numpy(scaler.transform(x[1].numpy())).float()
x[2] = torch.from_numpy(scaler.transform(x[2].numpy())).float()
학습 코드 구현
앞서와 똑같이 nn.Sequential을 활용하여 모델을 선언하고, 아담 옵티마이저에 등록합니다.
model = nn.Sequential(
nn.Linear(x[0].size(-1), 6),
nn.LeakyReLU(),
nn.Linear(6, 5),
nn.LeakyReLU(),
nn.Linear(5, 4),
nn.LeakyReLU(),
nn.Linear(4, 3),
nn.LeakyReLU(),
nn.Linear(3, y[0].size(-1)),
)
optimizer = optim.Adam(model.parameters())
모델 학습에 필요한 셋팅 값을 설정합니다.
n_epochs = 4000
batch_size = 256
print_interval = 100
앞서 이론 파트에서 우리가 원하는 모델은 가장 낮은 검증 손실 값validation loss을 갖는 모델이라고 이야기하였습니다. 따라서 매 에포크epoch마다 학습이 끝날 때, 검증 데이터셋을 똑같이 피드포워딩feed-forwarding하여 검증 데이터셋 전체에 대한 평균 손실 값을 구하고, 이전 에포크의 검증 손실 값과 비교하는 작업을 수행해야합니다. 만약 현재 에포크의 검증 손실 값이 이전 에포크 까지의 최저lowest 검증 손실 값보다 더 낮다면, 최저 검증 손실 값은 새롭게 갱신되고, 현재 에포크의 모델은 따로 저장되어야 할 것입니다. 또는 현재 에포크의 검증 손실 값이 이전 에포크 까지의 최저 검증 손실 값보다 크다면, 그냥 이번 에포크의 모델을 따로 저장할 필요 없이 넘어가면 됩니다. 그렇게 학습이 모두 끝났을 때, 정해진 에포크가 n_epochs 번 진행되는 동안 최저 검증 손실 값을 뱉어냈던 모델이 우리가 원하는 잘 일반화generaliztaion된 모델이라고 볼 수 있습니다. 따라서 학습이 종료되고 나면 최저 검증 손실 값의 모델을 다시 복원하고 사용자에게 반환하면 됩니다.
이를 위해서 다음 코드들은 최저 검증 손실을 추적하기 위한 변수 lowest_loss와 최저 검증 손실 값을 뱉어낸 모델을 저장하기 위한 변수 best_model을 미리 생성하는 모습입니다. 이때 best_model에 단순히 현재 모델을 저장한다면 얇은 복사shallow copy가 수행되어 주소값이 저장되므로, 깊은 복사deep copy를 통해 값 자체를 복사하여 저장해야 합니다. 이를 위해서 copy 패키지의 deepcopy 함수를 불러오는 것을 볼 수 있습니다.
from copy import deepcopy
lowest_loss = np.inf
best_model = None
early_stop = 100
lowest_epoch = np.inf
또한 학습 조기 종료early stopping을 위한 셋팅 값과, 가장 낮은 검증 손실 값을 뱉어낸 에포크를 저장하기 위한 변수 lowest_epoch도 선언합니다.
이제 본격 학습을 위한 for 반복문을 수행합니다. 이전까지의 실습과 달라진 점은 바깥 for 반복문의 후반부에 검증 작업을 위한 코드가 추가되었다는 점입니다. 따라서 코드가 굉장히 길어지게 되는데요. 설명을 위해 같은 for 반복문 안쪽에 있지만, 검증 작업을 위한 코드는 따로 떼어내보겠습니다. 그럼 앞서 우리가 보았던 코드와 상당히 유사한 코드가 나타납니다. 새롭게 추가된 코드는 학습/검증 손실 값 히스토리를 저장하기 위한 train_history와 valid_history 변수가 추가되었다는 것 정도입니다.
train_history, valid_history = [], []
for i in range(n_epochs):
# Shuffle before mini-batch split.
indices = torch.randperm(x[0].size(0))
x_ = torch.index_select(x[0], dim=0, index=indices)
y_ = torch.index_select(y[0], dim=0, index=indices)
# |x_| = (total_size, input_dim)
# |y_| = (total_size, output_dim)
x_ = x_.split(batch_size, dim=0)
y_ = y_.split(batch_size, dim=0)
# |x_[i]| = (batch_size, input_dim)
# |y_[i]| = (batch_size, output_dim)
train_loss, valid_loss = 0, 0
y_hat = []
for x_i, y_i in zip(x_, y_):
# |x_i| = |x_[i]|
# |y_i| = |y_[i]|
y_hat_i = model(x_i)
loss = F.mse_loss(y_hat_i, y_i)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += float(loss)
train_loss = train_loss / len(x_)
이처럼 학습 데이터셋을 미니배치로 나누어 한바퀴 학습하고 나면, 검증 데이터셋을 활용하여 검증 작업을 수행합니다. 학습과 달리 검증 작업은 역전파back-propagation를 활용하여 학습을 수행하지 않습니다. 따라서 그래디언트를 계산할 필요가 없기 때문에, torch.no_grad 함수를 호출하여 with 내부에서 검증 작업을 진행합니다. 그럼 그래디언트를 계산하기위한 배후 작업들이 없어지기 때문에 계산 오버헤드가 줄어들어 속도가 빨라지고 메모리 사용량도 줄어들게 됩니다.
그럼 with 내부를 살펴보겠습니다. split 함수를 써서 미니배치 크기로 나눠주는 것을 볼 수 있습니다. 앞서 이야기한 것처럼 검증 작업은 메모리 사용량이 적기 때문에, 검증 작업을 위한 미니배치 크기는 학습용보다 더 크게 가져가도 됩니다만, 간편함을 위해서 그냥 기존 학습용 미니배치 크기와 같은 크기를 사용하였습니다. 그리고 학습과 달리 셔플링shuffling 작업이 빠진 것을 볼 수 있습니다. 또한 for 반복문 내부에서도 피드포워드feed-forward만 있고, 역전파back-propagation 관련 코드는 없는 것을 볼 수 있습니다.
# You need to declare to PYTORCH to stop build the computation graph.
with torch.no_grad():
# You don't need to shuffle the validation set.
# Only split is needed.
x_ = x[1].split(batch_size, dim=0)
y_ = y[1].split(batch_size, dim=0)
valid_loss = 0
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = F.mse_loss(y_hat_i, y_i)
valid_loss += loss
y_hat += [y_hat_i]
valid_loss = valid_loss / len(x_)
# Log each loss to plot after training is done.
train_history += [train_loss]
valid_history += [valid_loss]
if (i + 1) % print_interval == 0:
print('Epoch %d: train loss=%.4e valid_loss=%.4e lowest_loss=%.4e' % (
i + 1,
train_loss,
valid_loss,
lowest_loss,
))
앞서와 같이 학습과 검증 작업이 끝나고 나면, 검증 손실 값을 기준으로 모델 저장 여부를 결정합니다. 우리가 원하는 것은 검증 손실을 낮추는 것입니다. 따라서 기존 최소 손실 값 변수 lowest_loss와 현재 검증 손실 값 valid_loss를 비교하여 최소 손실 값이 갱신될 경우, 현재 에포크의 모델을 저장합니다.[1] 또한 정해진 기간(early_stop 변수)동안 최소 검증 손실 값의 갱신이 없을 경우, 학습을 종료합니다. 이 조기 종료early stopping 파라미터 또한 하이퍼 파라미터임을 잊지 마세요.
if valid_loss <= lowest_loss:
lowest_loss = valid_loss
lowest_epoch = i
# 'state_dict()' returns model weights as key-value.
# Take a deep copy, if the valid loss is lowest ever.
best_model = deepcopy(model.state_dict())
else:
if early_stop > 0 and lowest_epoch + early_stop < i + 1:
print("There is no improvement during last %d epochs." % early_stop)
break
print("The best validation loss from epoch %d: %.4e" % (lowest_epoch + 1, lowest_loss))
# Load best epoch's model.
model.load_state_dict(best_model)
모든 작업이 수행되고 나면, for 반복문을 빠져나와 best_model에 저장되어있던 가중치 파라미터를 모델 가중치 파라미터로 복원합니다. 그럼 우리는 최소 검증 손실 값을 얻은 모델으로 되돌릴 수 있게 됩니다.
코드를 수행하면 다음과 같이 출력되는 것을 볼 수 있습니다. 539번째 에포크에서 최소 검증 손실 값을 얻었음을 알 수 있습니다. 만약 여러분이 보기에 손실 값이 좀 더 떨어질 여지가 있다면, 조기 종료 파라미터를 늘릴 수도 있습니다.
Epoch 100: train loss=3.4720e-01 valid_loss=3.3938e-01 lowest_loss=3.4056e-01
Epoch 200: train loss=3.0026e-01 valid_loss=2.9215e-01 lowest_loss=2.9067e-01
Epoch 300: train loss=2.9045e-01 valid_loss=2.8444e-01 lowest_loss=2.8279e-01
Epoch 400: train loss=2.8746e-01 valid_loss=2.8237e-01 lowest_loss=2.8207e-01
Epoch 500: train loss=2.8728e-01 valid_loss=2.8370e-01 lowest_loss=2.8160e-01
Epoch 600: train loss=2.8657e-01 valid_loss=2.8159e-01 lowest_loss=2.8090e-01
There is no improvement during last 100 epochs.
The best validation loss from epoch 539: 2.8090e-01
[1]: state_dict 함수가 현재 모델 파라미터를 key-value 형태로 주소값을 반환하기에, 그냥 변수에 state_dict 결과값을 저장할 경우 에포크가 끝날 때마다 best_model에 저장된 값이 바뀔 수 있습니다. 따라서 deepcopy를 활용하여 현재 모델의 가중치 파라미터를 복사하여 저장합니다.
손실 곡선 확인
그럼 이제 train_history, valid_history에 쌓인 손실 값들을 그림으로 그려 확인해보도록 하겠습니다. 이렇게 그림을 통해서 확인하면 화면에 프린트된 숫자들 보다 훨씬 쉽게 손실 값 추세를 확인할 수 있습니다.
plot_from = 10
plt.figure(figsize=(20, 10))
plt.grid(True)
plt.title("Train / Valid Loss History")
plt.plot(
range(plot_from, len(train_history)), train_history[plot_from:],
range(plot_from, len(valid_history)), valid_history[plot_from:],
)
plt.yscale('log')
plt.show()
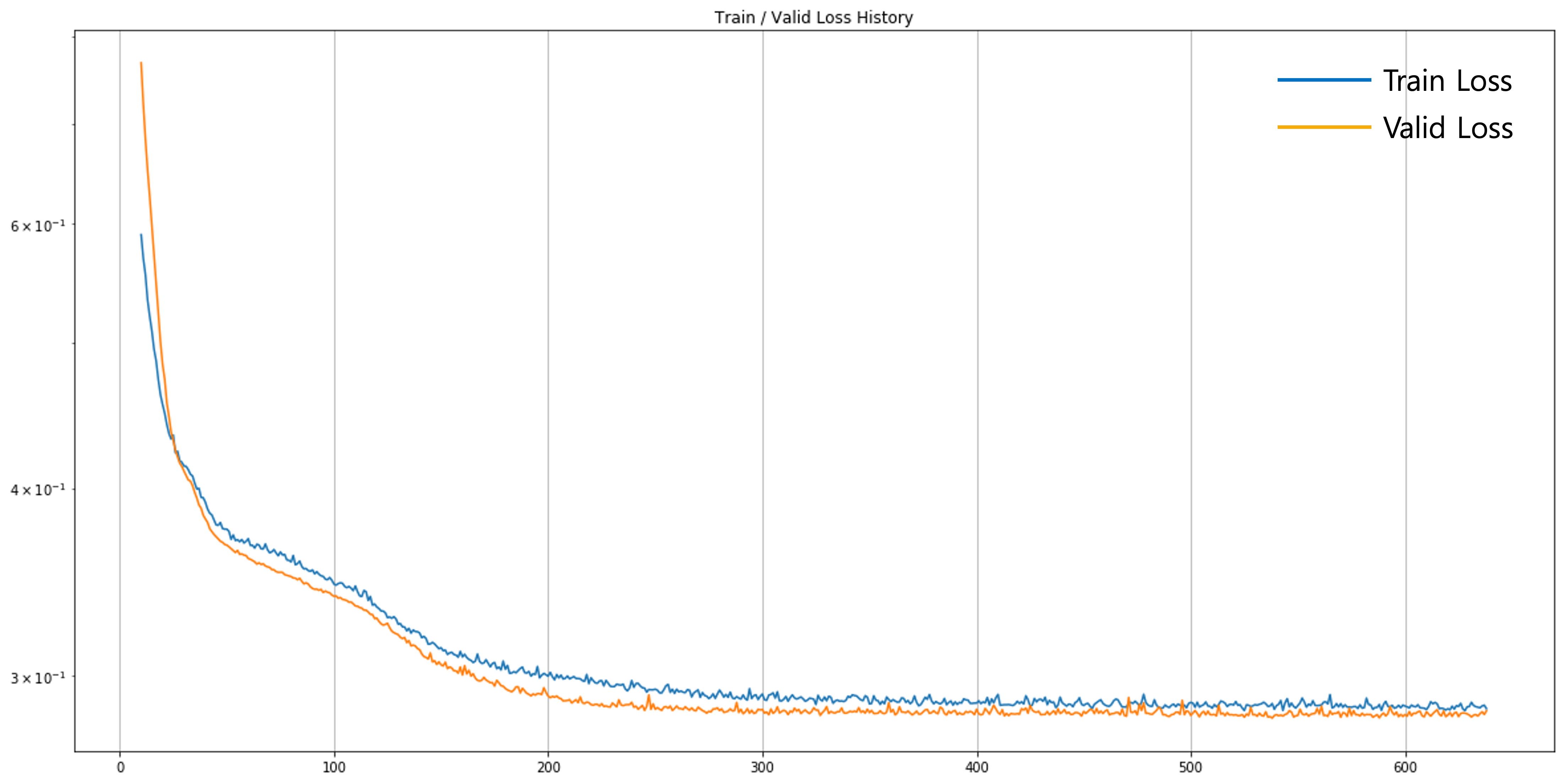
먼저 가장 눈에 띄는 부분은 대부분의 구간에서 검증 손실 값이 학습 손실 값 보다 낮다는 점입니다. 아무래도 검증 데이터셋은 학습 데이터셋에 비해서 일부에 불과하기 때문에 편향bias이 있을 수 있습니다. 따라서 우연하게 검증 데이터셋이 좀 더 쉽게 구성이 되었다면, 학습 데이터셋에 비해 더 낮은 손실 값을 가질 수도 있습니다. 만약 이 두 손실 값이 차이가 너무 크게 나지만 않는다면 크게 신경쓰지 않아도 됩니다.
그리고 검증 손실 값과 학습 손실 값의 차이가 학습 후반부로 갈수록 점점 더 줄어드는 것을 확인할 수 있습니다. 모델이 학습 데이터에만 존재하는 특성을 학습하는 과정이라고도 볼 수 있습니다. 하지만 어쨌든 검증 손실 값도 천천히 감소하고 있는 상황이므로, 온전한 오버피팅에 접어들었다고 볼 수는 없습니다.[2] 독자 분들도 조기 종료 파라미터 등을 바꿔가며 좀 더 낮은 검증 손실 값을 얻기 위한 튜닝을 해보시는 것도 좋습니다.
[2]: 조기 종료를 하지 않고 계속 학습시킨다면 오버피팅이 될 겁니다.
결과 확인
테스트 데이터셋에 대해서도 성능을 확인해보려 합니다. 우리의 최종 목표는 테스트 성능이 좋은 모델을 얻는 것이지만, 이 과정에서 학습 데이터셋과 검증 데이터셋만 활용할 수 있었고, 중간 목표는 검증 손실 값을 낮추는 것이었습니다. 이제 이렇게 얻어진 모델이 테스트 데이터셋에 대해서도 여전히 좋은 성능을 유지하는지 확인해보려 합니다. 다음의 코드를 보면 검증 작업과 거의 비슷하게 진행되는 것을 볼 수 있습니다. torch.no_grad 함수를 활용하여 with 내부에서 그래디언트 계산 없이 모든 작업이 수행됩니다. 또한 미니배치 크기로 split하여 for 반복문을 통해서 피드포워드feed-forward 합니다.
test_loss = 0
y_hat = []
with torch.no_grad():
x_ = x[2].split(batch_size, dim=0)
y_ = y[2].split(batch_size, dim=0)
for x_i, y_i in zip(x_, y_):
y_hat_i = model(x_i)
loss = F.mse_loss(y_hat_i, y_i)
test_loss += loss # Gradient is already detached.
y_hat += [y_hat_i]
test_loss = test_loss / len(x_)
y_hat = torch.cat(y_hat, dim=0)
sorted_history = sorted(zip(train_history, valid_history),
key=lambda x: x[1])
print("Train loss: %.4e" % sorted_history[0][0])
print("Valid loss: %.4e" % sorted_history[0][1])
print("Test loss: %.4e" % test_loss)
마지막으로 sorted 함수를 활용하여 가장 낮은 검증 손실 값과 이에 대응하는 학습 손실 값을 찾아서, 테스트 손실 값과 함께 출력합니다. 최종적으로 이 모델은 0.296 테스트 손실 값이 나오는 것으로 확인 되었습니다. 만약 여러분에 다른 방법론이나 모델 구조 변경등을 한다면, 0.296 테스트 손실 값이 나오는 모델이 베이스라인baseline 모델이 될 것입니다. 그럼 새로운 모델은 이 베이스라인을 이겨야 할 것입니다.[3]
Train loss: 2.8728e-01
Valid loss: 2.8090e-01
Test loss: 2.9679e-01
이번에는 앞서의 실습들과 마찬가지로 샘플들에 대한 정답과 예측 값을 페어플랏pair plot해보도록 하겠습니다. 앞서의 실습들과 다른 점은 테스트셋에 대해서만 그림을 그려본다는 점입니다.
df = pd.DataFrame(torch.cat([y[2], y_hat], dim=1).detach().numpy(),
columns=["y", "y_hat"])
sns.pairplot(df, height=5)
plt.show()

[3]: 따라서 정말 정당한 비교를 위해서는 매번 랜덤하게 학습/검증/테스트셋을 나누기보단, 아예 테스트셋을 따로 빼두는 것도 좋습니다.