실습: Adam Optimizer 적용하기
데이터 준비
이번 실습은 기존 캘리포니아 하우징 데이터셋에서 SGD를 Adam으로 교체하는 방법에 대해서 다루려고 합니다. 사실 코드의 대부분은 이전과 동일하며, 옵티마이저를 선언하는 부분만 바뀌게 되므로, 동일한 부분에 대해서는 길게 설명하지 않도록 하겠습니다.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_california_housing
필요한 패키지들과 데이터셋을 불러오고, 판다스Pandas에서 읽어들여, Target이라는 이름을 갖는 열에 출력 데이터를 넣어줍니다.
california = fetch_california_housing()
df = pd.DataFrame(california.data, columns=california.feature_names)
df["Target"] = california.target
df.tail()
그리고 앞서와 마찬가지로 표준 스케일링을 적용하여 입력 데이터를 정규화normalization합니다.
scaler = StandardScaler()
scaler.fit(df.values[:, :-1])
df.values[:, :-1] = scaler.transform(df.values[:, :-1])
df.tail()
학습 코드 구현
학습에 필요한 파이토치 관련 패키지들을 불러옵니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
그리고 넘파이Numpy로 되어 있는 데이터셋을 파이토치 텐서로 변환합니다.
data = torch.from_numpy(df.values).float()
x = data[:, :-1]
y = data[:, -1:]
print(x.shape, y.shape)
입력 데이터와 출력 데이터에 해당하는 열을 각각 슬라이싱하여 변수 x와 y에 집어넣고 크기를 출력해봅니다. 다음 출력 결과에서 알 수 있듯이, 20640개의 입출력 쌍 샘플들이 줄어졌고, 입력 샘플은 8차원의 벡터로 이루어지며 출력 샘플은 스칼라scalar 값으로 되어 있습니다.
torch.Size([20640, 8]) torch.Size([20640, 1])
이제 드디어 다른 코드가 나옵니다. 학습에 필요한 셋팅 값들을 선언해주는 부분인데, 이제 학습률learning rate이 필요없게 되었습니다. 눈에 띄도록 삭제하는 대신 일부러 주석처리하였습니다.
n_epochs = 4000
batch_size = 256
print_interval = 200
#learning_rate = 1e-2
그리고 nn.Sequential을 활용하여 똑같이 모델을 만듭니다.
model = nn.Sequential(
nn.Linear(x.size(-1), 6),
nn.LeakyReLU(),
nn.Linear(6, 5),
nn.LeakyReLU(),
nn.Linear(5, 4),
nn.LeakyReLU(),
nn.Linear(4, 3),
nn.LeakyReLU(),
nn.Linear(3, y.size(-1)),
)
이제 만든 모델을 옵티마이저에 등록할 차례입니다. 앞서는 optim.SGD 클래스를 통해서 모델을 학습하기 위한 옵티마이저 객체를 생성하였습니다. 이번에는 optim.Adam 클래스를 통해서 아담 옵티마이저를 선언합니다. 그리고 이때 모델 파라미터만 등록하되, 학습률은 인자로 넣어주지 않는 모습을 볼 수 있습니다.
# We don't need learning rate hyper-parameter.
optimizer = optim.Adam(model.parameters())
사실은 다음 그림과 같이 아담 옵티마이저 클래스도 생성시에 lr 인자를 입력으로 받을수 있긴 합니다. 하지만 이 학습률은 왠만해선 튜닝할 필요가 없습니다. 나중에 자연어처리나 영상처리, 음성인식 등 다양한 분야의 심화과정에서 쓰이는 트랜스포머Transformer를 사용하는 수준에 다다르면 그때서야 아담의 학습률을 튜닝해야 할 필요성이 생길겁니다. 당분간은 잊으셔도 좋습니다.

다음은 두 단계의 for 반복문을 통해 학습을 진행하는 코드입니다. 아담 옵티마이저의 도입으로 인해 바뀐 부분은 없습니다.
# |x| = (total_size, input_dim)
# |y| = (total_size, output_dim)
for i in range(n_epochs):
# Shuffle the index to feed-forward.
indices = torch.randperm(x.size(0))
x_ = torch.index_select(x, dim=0, index=indices)
y_ = torch.index_select(y, dim=0, index=indices)
x_ = x_.split(batch_size, dim=0)
y_ = y_.split(batch_size, dim=0)
# |x_[i]| = (batch_size, input_dim)
# |y_[i]| = (batch_size, output_dim)
y_hat = []
total_loss = 0
for x_i, y_i in zip(x_, y_):
# |x_i| = |x_[i]|
# |y_i| = |y_[i]|
y_hat_i = model(x_i)
loss = F.mse_loss(y_hat_i, y_i)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += float(loss)
y_hat += [y_hat_i]
total_loss = total_loss / len(x_)
if (i + 1) % print_interval == 0:
print('Epoch %d: loss=%.4e' % (i + 1, total_loss))
y_hat = torch.cat(y_hat, dim=0)
y = torch.cat(y_, dim=0)
# |y_hat| = (total_size, output_dim)
# |y| = (total_size, output_dim)
아담 옵티마이저 덕분인지 좀 더 낮은 손실 값을 보여주는 것을 볼 수 있습니다. 만약 여러분이 SGD를 사용했다면 비슷한 손실 값을 얻기 위해서는 여러번의 튜닝이 필요했거나, 학습 중에 학습률을 바꿔주는 등의 다양한 트릭이 필요했을 수도 있습니다. 하지만 아담 옵티마이저를 사용하여 훨씬 편리하고 빠르게 더 낮은 손실 값에 수렴할 수 있게 되었습니다.
Epoch 200: loss=3.1430e-01
Epoch 400: loss=3.0689e-01
Epoch 600: loss=3.0328e-01
Epoch 800: loss=3.0001e-01
Epoch 1000: loss=2.9695e-01
Epoch 1200: loss=2.9685e-01
Epoch 1400: loss=2.9601e-01
Epoch 1600: loss=2.9575e-01
Epoch 1800: loss=2.9495e-01
Epoch 2000: loss=2.9482e-01
Epoch 2200: loss=2.9314e-01
Epoch 2400: loss=2.9309e-01
Epoch 2600: loss=2.9253e-01
Epoch 2800: loss=2.9197e-01
Epoch 3000: loss=2.9228e-01
Epoch 3200: loss=2.9151e-01
Epoch 3400: loss=2.9211e-01
Epoch 3600: loss=2.9156e-01
Epoch 3800: loss=2.9199e-01
Epoch 4000: loss=2.9094e-01
결과 확인
df = pd.DataFrame(torch.cat([y, y_hat], dim=1).detach().numpy(),
columns=["y", "y_hat"])
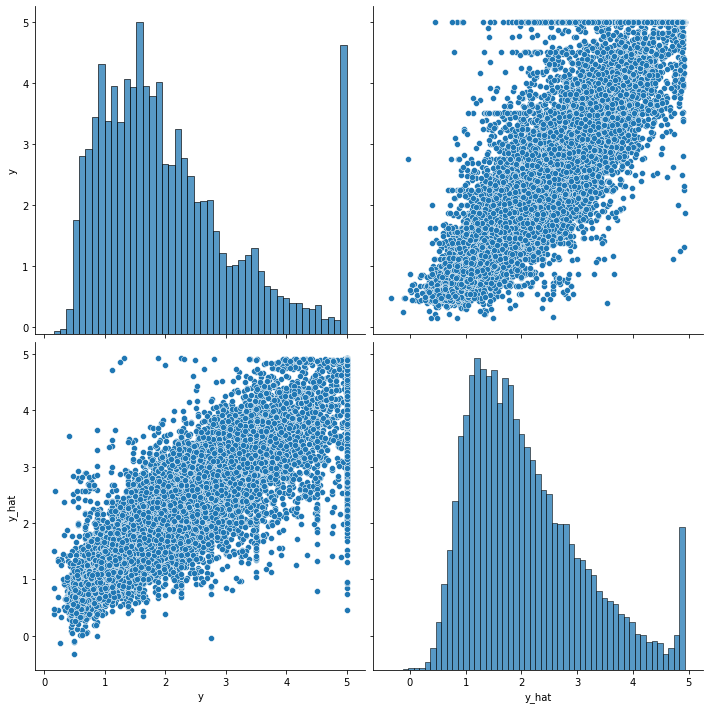
sns.pairplot(df, height=5)
plt.show()
재미있게도 이번 실습에서는 y_hat에서 가장 큰 값에서의 분포가 마치 실제 정답 y처럼 튀어나와있는 것을 확인할 수 있고, 이로인해 이번 예측이 좀 더 잘 이루어졌다고 볼 수 있습니다.