실습: 로지스틱 회귀

데이터 준비

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

필요한 라이브러리와 데이터셋을 불러옵니다.

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

print(cancer.DESCR)

위스콘신 유방암^{Breast cancer wisconsin} 데이터셋은 30개의 속성을 가지며, 이를 통해 유방암 여부를 예측해야 합니다. 앞서 선형 회귀와 마찬가지로 판다스^Pandas로 데이터를 변환합니다. 여기서는 출력 값을 class 속성으로 저장합니다.

df = pd.DataFrame(cancer.data, columns=cancer.feature_names)
df['class'] = cancer.target

이 데이터셋의 설명을 잘 읽어보면 속성이 30개인 이유는 각 10개 속성의 평균^mean, 표준편차^{standard error}, 최악^worst 값을 나타내고 있기 때문임을 알 수 있습니다. 따라서 평균과 표준편차 그리고 최악 속성들만 따로 모아서 class 속성과 비교하는 페어 플랏^{pair plot} 그리도록 하겠습니다.

sns.pairplot(df[['class'] + list(df.columns[:10])])
plt.show()

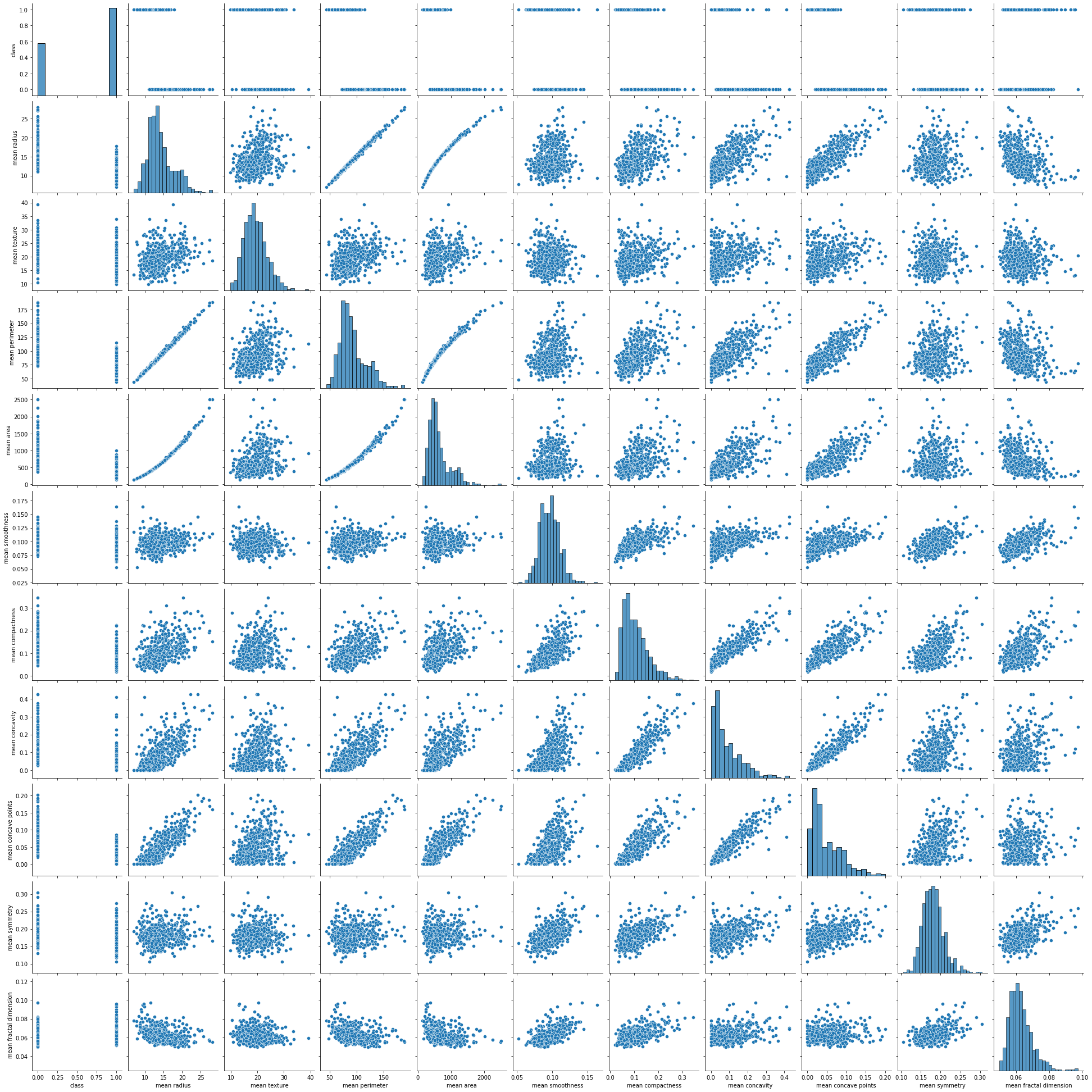
여기서 맨 윗 줄만 떼어서 자세히 볼까요?

각 속성별 샘플의 점들이 0번 클래스에 해당하는 경우 아래쪽, 1번 클래스에 해당하는 경우 윗쪽으로 찍혀 있는 것을 볼 수 있습니다. 만약 이 점들의 클래스별 그룹이 명확하게 특정 값을 기준으로 나눠진다면 좋은 것을 볼 수 있습니다. 마찬가지로 다른 속성들에 대해서도 페어 플랏을 그려줍니다.

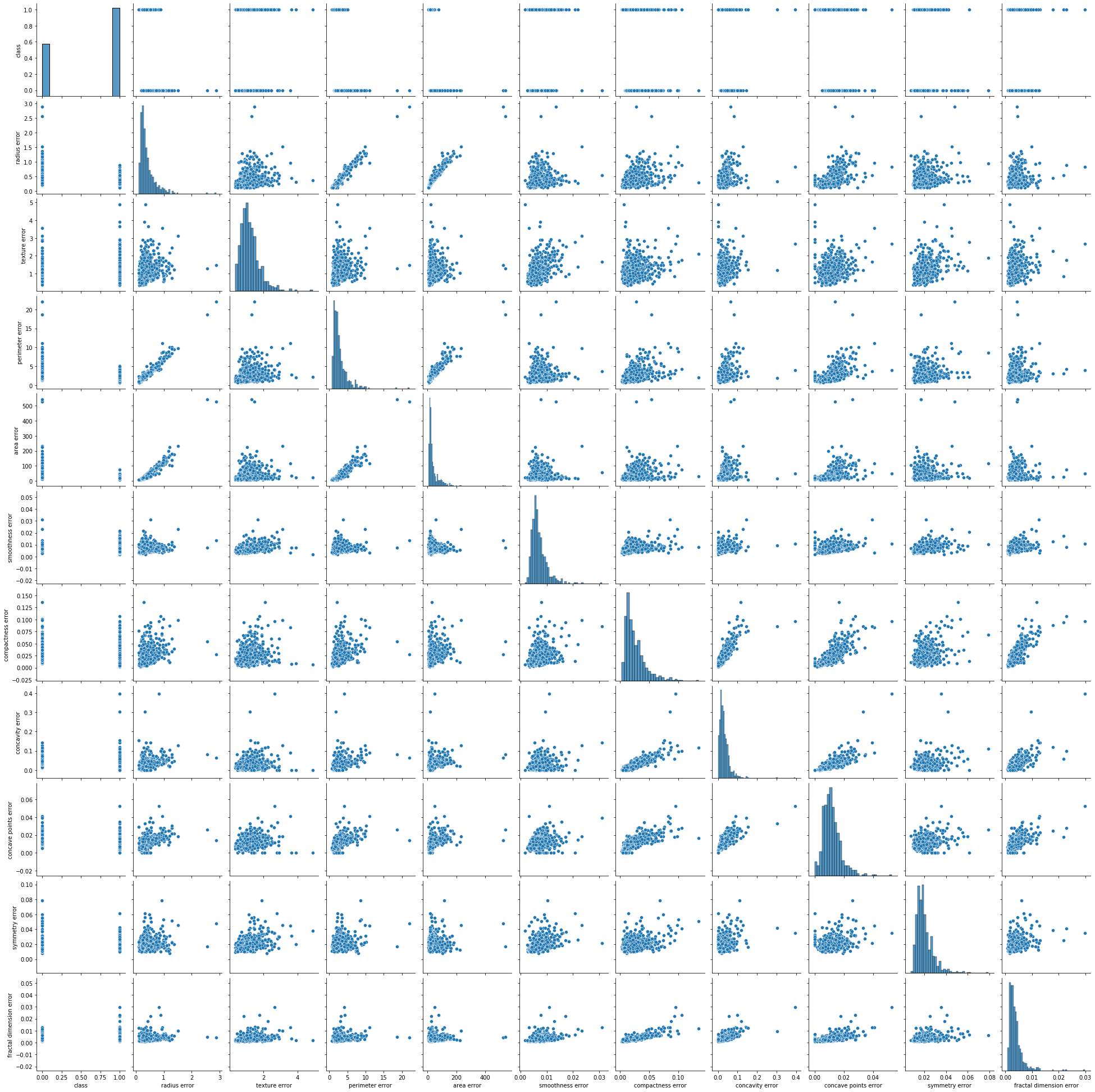
sns.pairplot(df[['class'] + list(df.columns[10:20])])
plt.show()

sns.pairplot(df[['class'] + list(df.columns[20:30])])
plt.show()

이렇게 그림을 그려놓고 보니, 대략적으로 정답 클래스와의 관계를 파악할 수 있습니다. 살펴보면 표준편차 속성의 경우에는 크게 도움이 되지 않는 것 같습니다. 이번에는 이 그림들을 바탕으로 몇 개 골라서 좀 더 이쁘게 그려보도록 하겠습니다.

cols = ["mean radius", "mean texture",
        "mean smoothness", "mean compactness", "mean concave points",
        "worst radius", "worst texture",
        "worst smoothness", "worst compactness", "worst concave points",
        "class"]

for c in cols[:-1]:
    sns.histplot(df, x=c, hue=cols[-1], bins=50, stat='probability')
    plt.show()

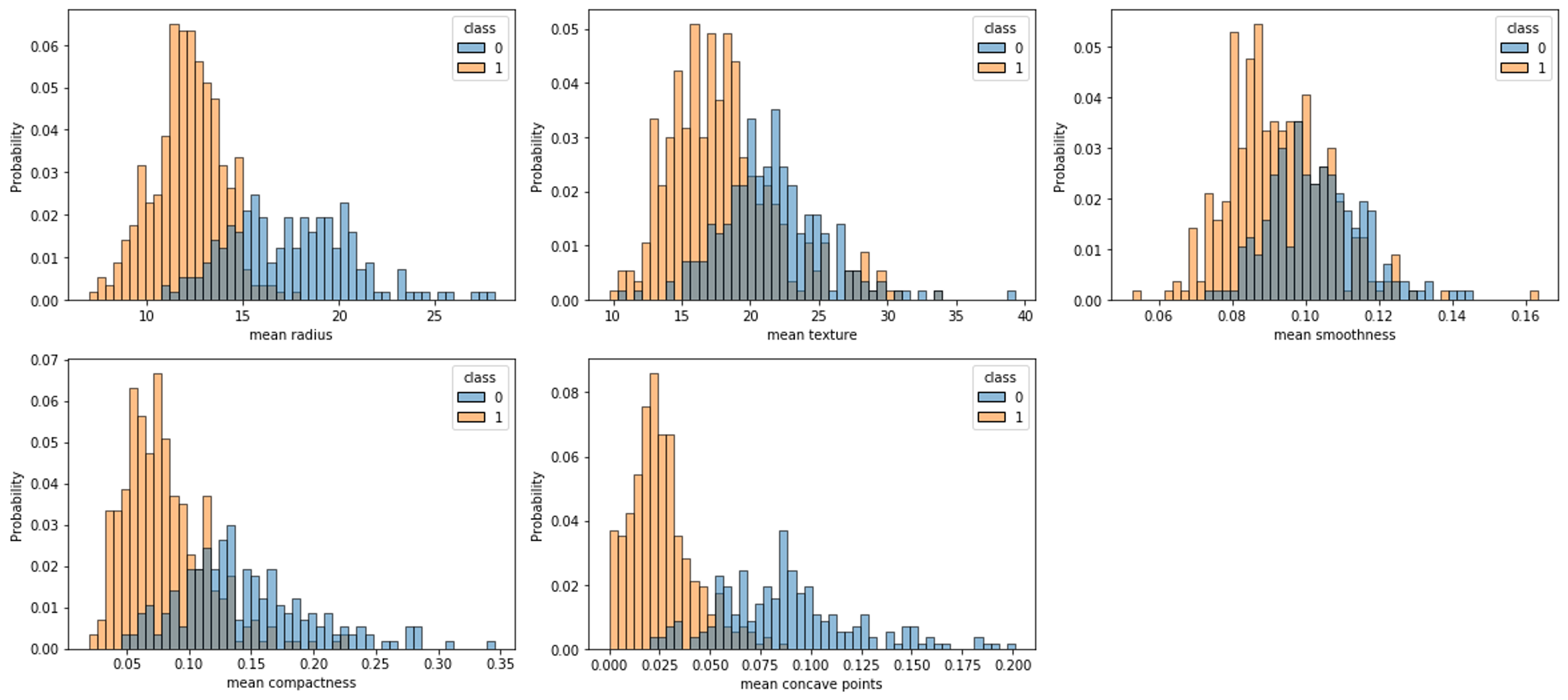
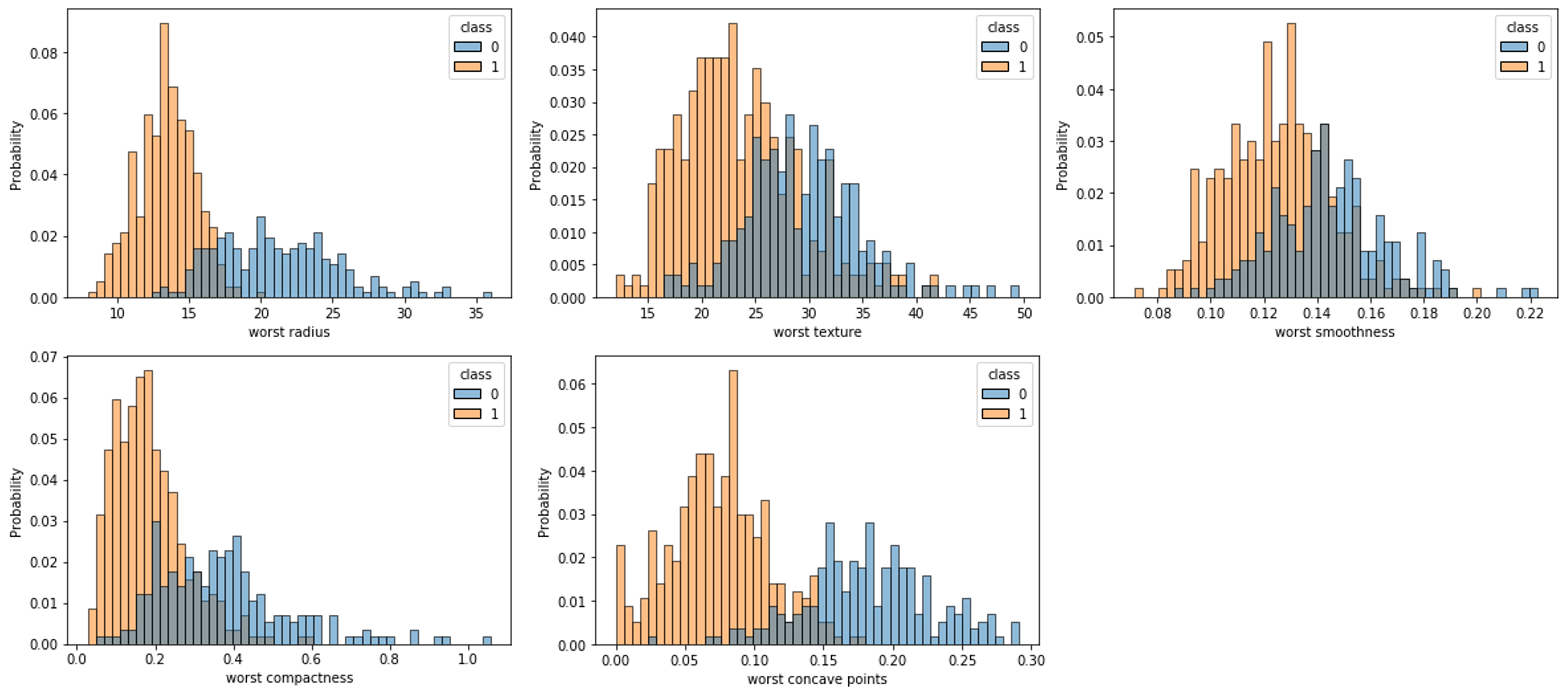
클래스에 따른 속성별 분포를 나타낸 것입니다. 0번 클래스는 파란색, 1번 클래스는 주황색으로 표시되었음을 볼 수 있습니다. 겹치는 영역이 적을수록 좋은 속성이라고 볼 수 있습니다. 완벽하게 두 클래스를 나눠주는 속성은 없지만, 부족한 부분은 다른 속성에서 보완받을 수 있을 것이라 믿고, 해당 속성들을 가지고 로지스틱 회귀를 진행해보도록 하겠습니다.

학습 코드 구현

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

data = torch.from_numpy(df[cols].values).float()

data.shape

# Split x and y.
x = data[:, :-1]
y = data[:, -1:]

print(x.shape, y.shape)

앞서 선형회귀와 똑같은 방식으로 텐서 x와 텐서 y를 가져옵니다. 그리고 학습에 필요한 설정 값들을 정해줍니다.

# Define configurations.
n_epochs = 200000
learning_rate = 1e-2
print_interval = 10000

이제 모델을 준비할 차례입니다. 앞서 선형 회귀에서는 선형 계층^{linear layer} 하나만 필요했던 것과 달리, 이번에는 시그모이드^sigmoid 함수도 모델이 포함되어야 합니다. 따라서 nn.Module을 상속받아 클래스를 정의하고, 내부에 필요한 계층들을 소유하도록 합니다.

앞서 배웠던 것처럼 nn.Module을 상속받은 자식 클래스를 정의할 때는 보통 두 개의 함수(메서드^method)를 오버라이드^override합니다. __init__ 함수를 통해 모델을 구성하는데 필요한 내부 모듈(e.g. 선형 계층)들을 미리 선언해두고, forward 함수에서는 미리 선언된 내부 모듈들을 활용해 계산을 수행합니다.

# Define costum model.
class MyModel(nn.Module):
    
    def __init__(self, input_dim, output_dim):
        self.input_dim = input_dim
        self.output_dim = output_dim
        
        super().__init__()
        
        self.linear = nn.Linear(input_dim, output_dim)
        self.act = nn.Sigmoid()
        
    def forward(self, x):
        # |x| = (batch_size, input_dim)
        y = self.act(self.linear(x))
        # |y| = (batch_size, output_dim)
        
        return y

이제 정의한 나만의 로지스틱 회귀 모델 클래스를 생성하고, BCE 손실함수, 옵티마이저도 준비합니다. 선형회귀와 마찬가지로 모델의 입력 크기는 텐서 x의 마지막 차원의 크기가 되고, 출력 크기는 텐서 y의 마지막 차원의 크기가 됩니다.

model = MyModel(input_dim=x.size(-1),
                output_dim=y.size(-1))
crit = nn.BCELoss() # Define BCELoss instead of MSELoss.

optimizer = optim.SGD(model.parameters(),
                      lr=learning_rate)

이제 학습을 위한 준비가 끝났습니다. 선형회귀와 똑같은 코드로 학습을 진행할 수 있습니다.

for i in range(n_epochs):
    y_hat = model(x)
    loss = crit(y_hat, y)
    
    optimizer.zero_grad()
    loss.backward()
    
    optimizer.step()
    
    if (i + 1) % print_interval == 0:
        print('Epoch %d: loss=%.4e' % (i + 1, loss))

결과를 확인하면 점점 손실 값이 작아지는 것을 볼 수 있습니다.^[1]

Epoch 10000: loss=2.7814e-01
Epoch 20000: loss=2.2899e-01
Epoch 30000: loss=1.9974e-01
Epoch 40000: loss=1.8068e-01
Epoch 50000: loss=1.6739e-01
Epoch 60000: loss=1.5761e-01
Epoch 70000: loss=1.5011e-01
Epoch 80000: loss=1.4418e-01
Epoch 90000: loss=1.3937e-01
Epoch 100000: loss=1.3538e-01
Epoch 110000: loss=1.3202e-01
Epoch 120000: loss=1.2914e-01
Epoch 130000: loss=1.2665e-01
Epoch 140000: loss=1.2447e-01
Epoch 150000: loss=1.2255e-01
Epoch 160000: loss=1.2084e-01
Epoch 170000: loss=1.1930e-01
Epoch 180000: loss=1.1792e-01
Epoch 190000: loss=1.1666e-01
Epoch 200000: loss=1.1551e-01

[1]: 모델 마지막의 시그모이드로 인해 그래디언트가 작아지므로 좀 더 수렴에 오래걸리는 것을 볼 수 있습니다.

결과 확인

지금은 분류 문제이므로 분류 예측 결과에 대해서 정확도로 평가가 가능합니다. 그럼 마지막으로 모델을 통과^feed-forward하여 얻은 y_hat과 y를 비교하여 정확도를 계산하여 보겠습니다.

correct_cnt = (y == (y_hat > .5)).sum()
total_cnt = float(y.size(0))

print('Accuracy: %.4f' % (correct_cnt / total_cnt))

이번 학습에서는 0.9649의 정확도가 나오는 것을 볼 수 있습니다.^[2] 좀 전에 데이터를 분석하던 방법을 활용하여 예측된 결과 값들이 분포도 살펴볼 수 있습니다.

df = pd.DataFrame(torch.cat([y, y_hat], dim=1).detach().numpy(),
                  columns=["y", "y_hat"])

sns.histplot(df, x='y_hat', hue='y', bins=50, stat='probability')
plt.show()

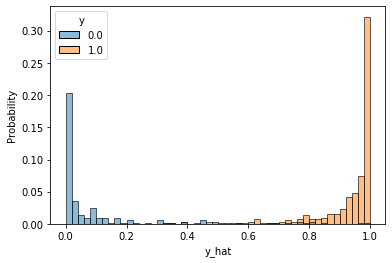
만약 각 클래스별 분포가 양 극단으로 완벽하게 치우쳐져 나타난다면 모델이 매우 예측을 잘하고 있는 것이 됩니다. 지금은 그정도는 아니지만 대부분의 값들이 양 쪽에 치우쳐져 나타나고 있는 것을 볼 수 있으며, 일부 샘플들이 중간에 뒤엉켜 혼재하고 있음을 확인할 수 있습니다.

[2]: 학습 할 때마다 성능은 달라질 수 있습니다.