실습: 선형 회귀

데이터 준비

먼저 실습에 필요한 라이브러리들을 설치합니다.

!pip install matplotlib seaborn pandas sklearn

그리고 필요한 라이브러리들을 불러옵니다.

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

이번에는 이번 실습에서 사용할 데이터셋을 불러옵니다.

from sklearn.datasets import load_boston
boston = load_boston()

print(boston.DESCR)

그럼 보스턴 주택 가격 데이터셋^{Boston house prices dataset}에 대한 설명이 자세히 출력될 것입니다. 이 데이터셋은 506개의 샘플을 가지고 있으며, 13개의 속성^attribute들과 이에 대한 타겟 값을 갖고 있습니다.

간단한 탐험적 데이터 분석^{exploratory data analysis, EDA}을 위해서 판다스^Pandas 데이터 프레임으로 변환 후, 데이터 일부를 확인합니다.

df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["TARGET"] = boston.target
df.tail()

각 속성의 분포와 속성 사이의 선형적 관계 유무를 파악하기 위해서 페어 플랏^{pair plot}을 그려봅니다.

sns.pairplot(df)
plt.show()

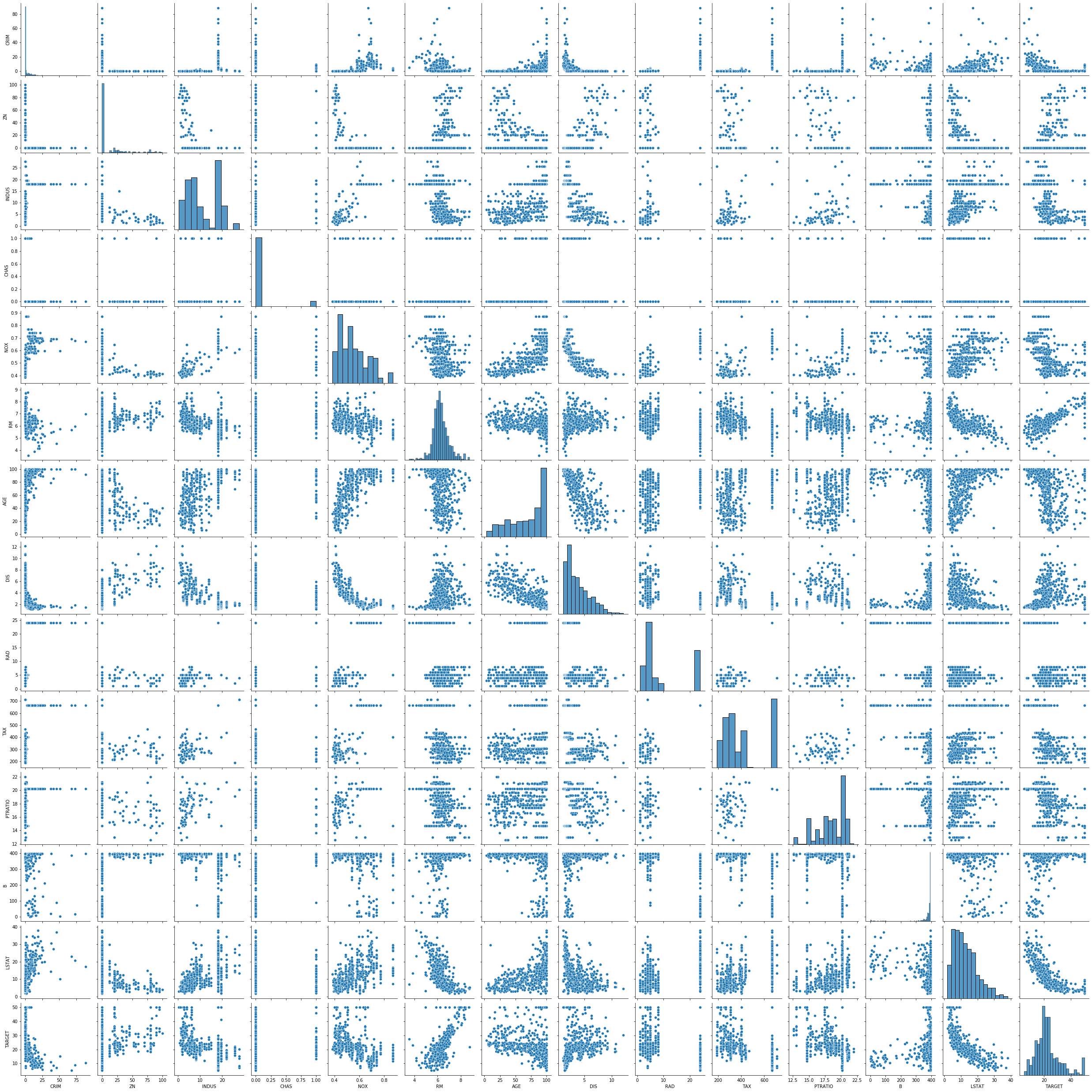
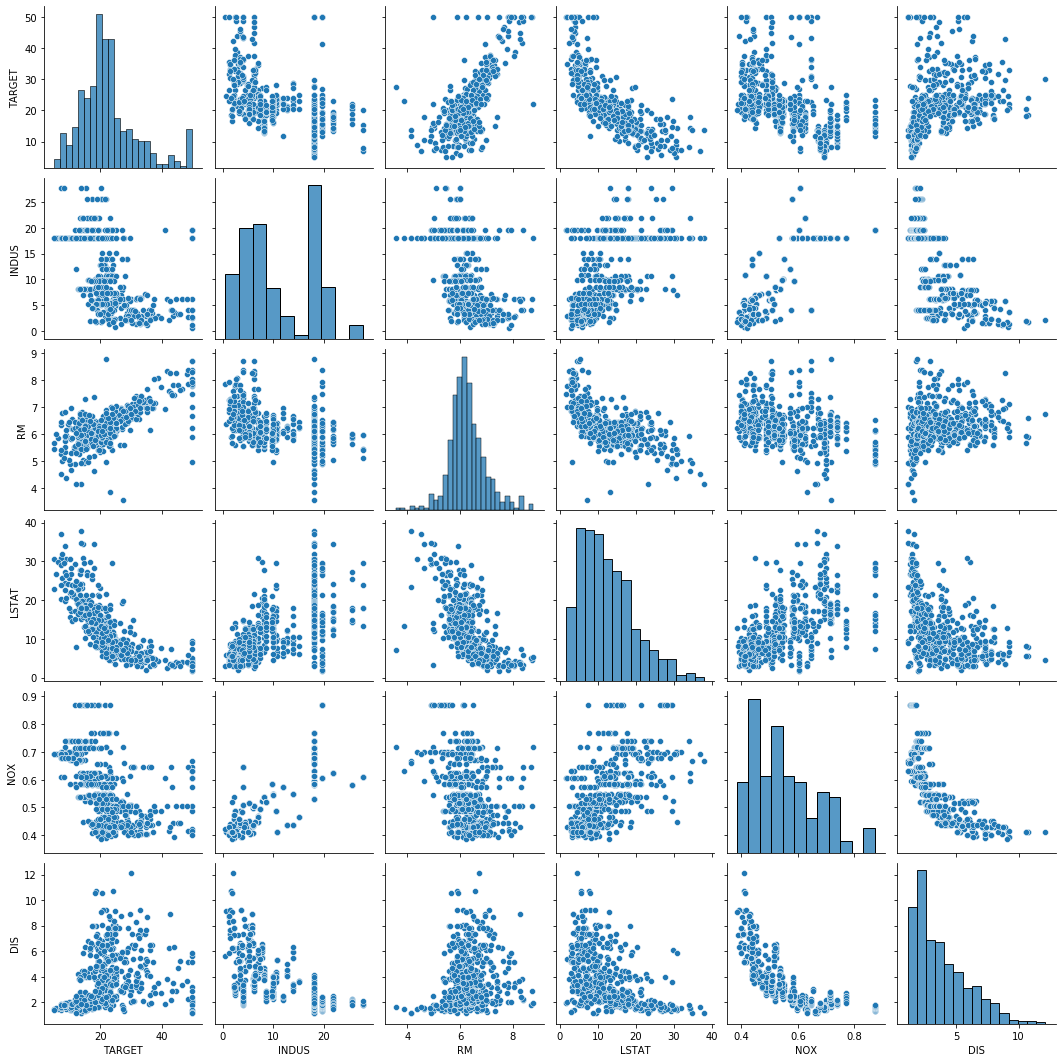
TARGET 속성에 대응되는 맨 마지막줄을 살펴보면 일부 속성들이 TARGET 속성과 약간의 선형적 관계를 띄는 것을 볼 수 있습니다. 선형적 관계를 띄는 것으로 보이는 일부 속성을 추려내서 다시 페어 플랏을 그려봅니다. 이번에는 그림의 맨 첫 줄이 TARGET 속성과 대응하여 그린 것입니다.

cols = ["TARGET", "INDUS", "RM", "LSTAT", "NOX", "DIS"]
sns.pairplot(df[cols])
plt.show()  

학습 코드 구현

>>> import torch
>>> import torch.nn as nn
>>> import torch.nn.functional as F
>>> import torch.optim as optim

Numpy 데이터를 파이토치 실수형 텐서로 변환합니다.

>>> data = torch.from_numpy(df[cols].values).float()
>>> data.shape
torch.Size([506, 6])

이제 이 데이터를 입력 $x$ 와 출력 $y$ 로 나눠봅니다.

>>> y = data[:, :1]
>>> x = data[:, 1:]
>>> print(x.shape, y.shape)
torch.Size([506, 5]) torch.Size([506, 1])

학습에 필요한 설정 값들을 정합니다.

>>> n_epochs = 2000
>>> learning_rate = 1e-3
>>> print_interval = 100

모델을 생성합니다. 텐서 x의 마지막 차원의 크기를 선형 계층의 입력 크기로 주고, 텐서 y의 마지막 차원의 크기를 선형 계층의 출력 크기로 줍니다.

>>> model = nn.Linear(x.size(-1), y.size(-1))
>>> print(model)
Linear(in_features=5, out_features=1, bias=True)

그리고 옵티마이저^optimizer를 생성합니다. 앞서 경사하강법^{gradient descent}를 실습하였을 때, 직접 경사하강법을 구현하였지만, 사실 파이토치에서는 옵티마이저 클래스를 제공하여 해당 작업을 대신 수행합니다. backward 함수를 호출 한 후, 옵티마이저 객체에서 step 함수를 호출하면, 경사하강을 1번 수행합니다.

>>> optimizer = optim.SGD(model.parameters(),
...                       lr=learning_rate)

그럼 이제 학습을 진행할 준비를 마쳤습니다. 다음 코드를 통해 정해진 에포크^epoch^[1]만큼 for 반복문을 통해 최적화를 수행합니다.

for i in range(n_epochs):
    y_hat = model(x)
    loss = F.mse_loss(y_hat, y)
    
    optimizer.zero_grad()
    loss.backward()
    
    optimizer.step()
    
    if (i + 1) % print_interval == 0:
        print('Epoch %d: loss=%.4e' % (i + 1, loss))

다음은 학습 코드를 실행한 결과입니다. 100 에포크마다 손실값^loss이 출력되는 것을 볼 수 있으며, 그 값은 계속해서 줄어들다가 29 부근^[2]에서 수렴하고 있음을 알 수 있습니다.

Epoch 100: loss=4.1877e+01
Epoch 200: loss=3.6177e+01
Epoch 300: loss=3.3046e+01
Epoch 400: loss=3.1282e+01
Epoch 500: loss=3.0288e+01
Epoch 600: loss=2.9727e+01
Epoch 700: loss=2.9410e+01
Epoch 800: loss=2.9232e+01
Epoch 900: loss=2.9131e+01
Epoch 1000: loss=2.9074e+01
Epoch 1100: loss=2.9041e+01
Epoch 1200: loss=2.9022e+01
Epoch 1300: loss=2.9012e+01
Epoch 1400: loss=2.9005e+01
Epoch 1500: loss=2.9001e+01
Epoch 1600: loss=2.8999e+01
Epoch 1700: loss=2.8997e+01
Epoch 1800: loss=2.8996e+01
Epoch 1900: loss=2.8995e+01
Epoch 2000: loss=2.8994e+01

[1]: 한 번의 에포크는 학습 데이터 전체를 한번 모델이 학습하는 것을 가리킵니다.

[2]: 학습할 때마다 결과는 달라질 수 있습니다.

결과 확인

그럼 학습이 잘 수행되었는지 확인해볼 차례입니다. 사실 2.9라는 손실 값을 통해서도 학습이 진행된 정도를 파악할 수 있었지만, 사실 해당 값만 놓고 보아서는 느낌이 잘 오지 않기 때문에 시각화를 통해 다시 한번 확인해보고자 합니다. 마지막으로 모델을 통과^feed-forward한 y_hat을 가져와서 실제 y와 비교하기위한 페어 플랏을 그려봅니다.

df = pd.DataFrame(torch.cat([y, y_hat], dim=1).detach_().numpy(),
                  columns=["y", "y_hat"])

sns.pairplot(df, height=5)
plt.show()

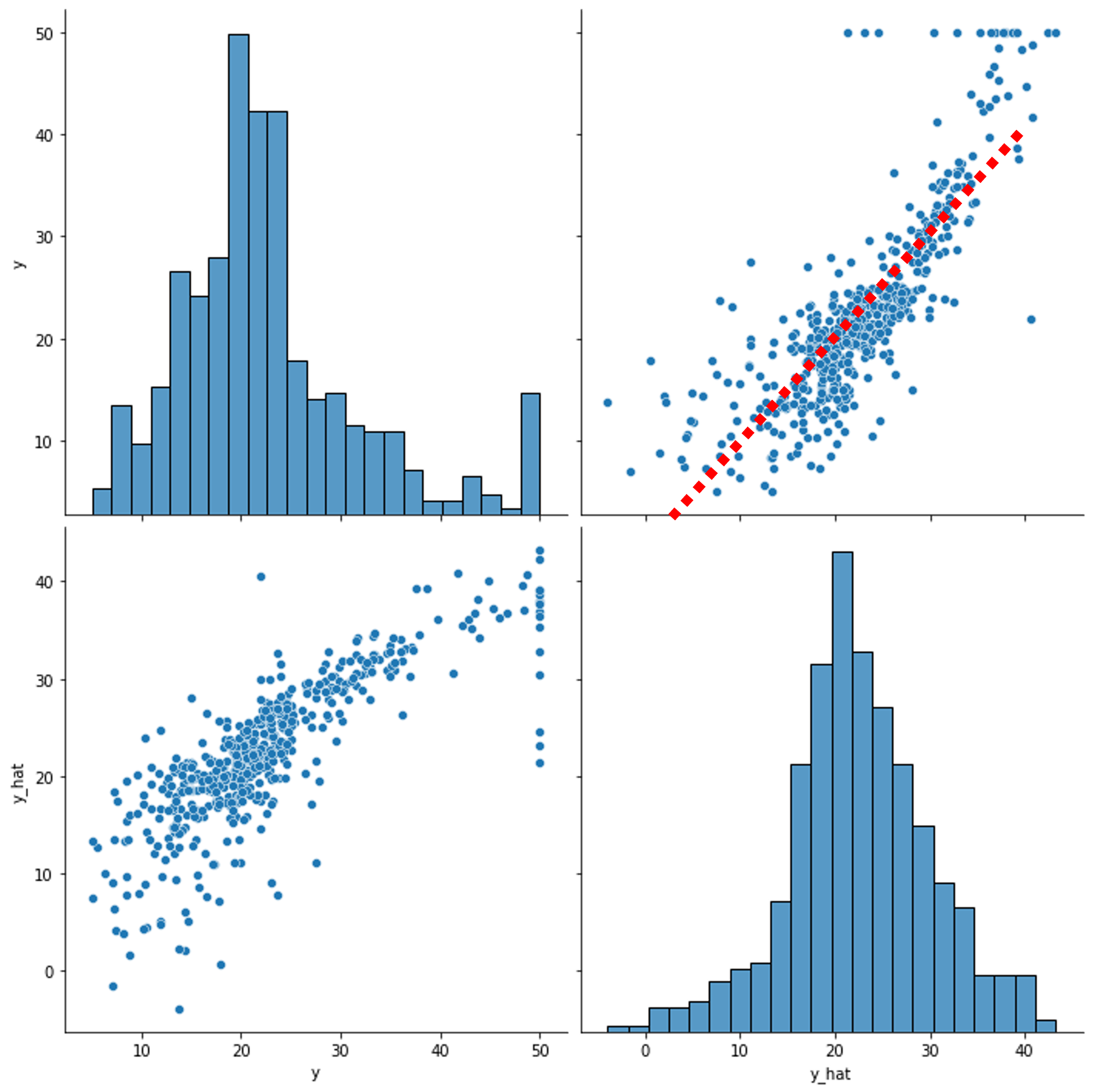
왼쪽 위에 그려진 y의 분포와 오른쪽 아래에 그려진 y_hat의 분포가 약간은 다르게 나오는 것을 볼 수 있습니다. 하지만 오른쪽 위에 그려진 y와 y_hat의 직접 비교에서는 대부분의 점들이 빨간색 점선 부근에서 나타나는 것을 볼 수 있습니다.