텐서란?

텐서^tensor는 딥러닝에서 가장 기본이 되는 단위 중 하나입니다. 스칼라^scalar, 벡터^vector, 행렬^matrix, 그리고 텐서를 통해 우리는 딥러닝의 연산을 수행할 수 있습니다. 다음 그림은 스칼라, 벡터, 행렬, 텐서의 관계를 나타냅니다.

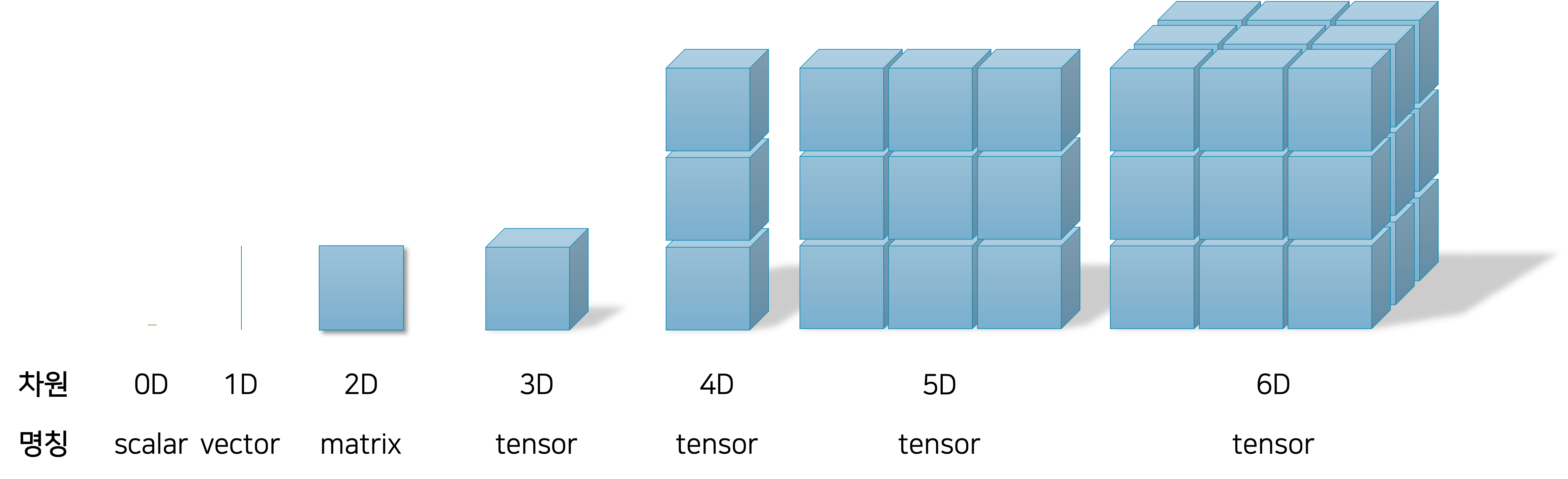
각 값을 메모리에 저장할 때, 스칼라는 하나의 변수로 나타낼 수 있고, 벡터는 1차원의 배열로 나타낼 수 있습니다. 그리고 행렬은 2차원의 배열로 나타내며, 텐서부터는 3차원 이상의 배열로 나타냅니다. 2차원까지는 각각 명칭이 따로 있지만, 3차원부터는 모두 텐서라고 묶어 부르는 점에 유의하세요.

행렬의 표현

우리가 다룰 대부분의 값들은 보통은 float 타입이나 double 타입으로 표현되느 실수^{real number}입니다. 그럼 실수들로 채워진 행렬은 다음 그림과 같이 표현할 수 있습니다.

행렬 $x$ 는 $k$ 개의 행^row과 $n$ 개의 열^column으로 이루어져 있으며 값들은 모두 실수로 이루어져 있습니다. 이것을 수식으로 표현하면 다음과 같습니다.

공신력 있는 정식 표현은 아닙니다만, 표기의 편의성을 위해서 이 책에서는 이 행렬을 아래와 같이 병기하기로 합니다.

이것은 마치 나중에 배울 텐서에 대한 size() 함수를 호출한 것과 같다고 보면 됩니다. 그리고 앞서 그림에서 첫 번째 차원^dimension $k$ 가 세로축의 크기를 나타내고 있는 것에 주목해주세요. 이어서 두 번째 차원 $n$ 이 가로축의 크기를 나타내고 있습니다.

텐서의 표현

이번에는 행렬에 이어서 텐서의 표현에 대해서도 살펴보도록 하겠습니다. 다음의 그림은 실수로 이루어진 $k\times{n}\times{m}$ 차원의 텐서를 나타냅니다.

중요한 점은 마찬가지로 첫 번째 차원 $k$ 가 세로축의 크기를 나타내며, 이후 차례대로 $n$ 이 가로축의 차원을 나타내고, $m$ 이 마지막 남은 축의 차원을 나타냅니다. 이렇게 순서대로 나타내라고 약속이 정해져 있는 것은 아닙니다. 하지만 여러분들이 앞으로 딥러닝을 공부할 때, 이렇게 시각화를 할 일이 굉장히 많아질텐데요. 그럼 각 차원의 순서가 뒤죽박죽 되는 것보단, 일괄적으로 이처럼 자신만의 약속을 만들어 표현하는 것이 훨씬 효율적입니다. 따라서 저는 독자분들이 앞서 그림과 같이 각 축에 대해서 일괄적으로 순서대로 차원을 할당하시길 권장합니다.

앞으로 우리가 자주 만날 행렬/텐서의 모양들

앞으로 여러분은 딥러닝을 통해 다양한 분야의 많은 문제들을 풀어나갈 것입니다. 이때 데이터의 도메인에 따라서 문제들을 나눠 볼 수 있습니다. 각 도메인에 따라서 우리가 자주 다루게 될 텐서의 형태 또한 상이합니다. 이번에는 각 도메인 별 자주 만날 행렬/텐서의 형태에 대해서 이야기해보겠습니다.

데이터 사이언스: 테이블 형태의 데이터셋

데이터 사이언스 또는 데이터 분석을 수행할때에는 주로 테이블 형태^tabular의 데이터셋을 다루게 됩니다. 한마디로 엑셀 파일을 생각하면 쉽습니다. 엑셀 파일에는 여러개의 열^column이 존재하고, 각 샘플들은 각 열에 대해서 값을 가지며 하나의 행^row을 이루게 됩니다. 테이블 형태의 데이터를 텐서로 나타내면 다음과 같습니다.

$N$ 개의 샘플이 존재하므로, $N$ 이 세로축의 크기를 나타냅니다. $n$ 은 열의 갯수를 나타내고, 가로축의 크기를 나타냅니다. 열은 피쳐^feature라고 부르며, 각 샘플의 고유한 속성을 설명하는 값을 담고 있습니다. 만약 피쳐의 값들이 비슷한 샘플끼리는 비슷한 속성을 가진다고 볼 수 있습니다.

그리고 그림에서 빨간색 점선으로 둘러싸인 부분은 하나의 샘플을 나타냅니다. 전체 데이터가 $N\times{n}$ 행렬이므로, 하나의 샘플은 $n$ 개의 요소를 갖는 $n$ 차원의 벡터가 됩니다. $n$ 차원의 벡터가 $N$ 개 모이므로, $N\times{n}$ 차원의 행렬이 되겠지요.

여기서 재미있는 점은 딥러닝은 병렬^parallel연산을 수행한다는 것입니다. 만약에 $N$ 개의 샘플을 신경망에 통과시킨다면, $N$ 번의 연산을 각각 수행하는 것이 아닌, 메모리의 크기가 허용되는 한에서 덩어리로 통과시키게 됩니다. 예를 들어, $k$ 개의 샘플 벡터들을 통과시킨다면, 이를 위해서는 $k$ 의 샘플들은 $k\times{n}$ 의 행렬이 되어 신경망을 통과하게 될 것입니다. 다음의 그림은 이러한 병렬 연산을 위한 행렬을 빨간 점선으로 나타낸 것입니다.

빨간색 점선 부분의 $k\times{n}$ 행렬은 전체 데이터셋 $N\times{n}$ 행렬에서 슬라이싱^slicing을 통해 얻는다고 봐도 될 것입니다.

자연어처리: 문장 데이터셋

이번에는 자연어처리에 대해서 살펴보도록 하겠습니다. 자연어처리가 주로 다루는 데이터의 대상은 문장일 것입니다. 문장은 단어(토큰^token)들이 모여서 이루어진, 시퀀셜^sequential 데이터입니다. 시퀀셜 데이터는 내부 토큰들의 출현과 순서 관계에 의해서 속성의 정의됩니다.

단어(토큰)는 각각이 의미를 지니기 때문에, 의미를 나타내기 위한 벡터로 표현됩니다. 우리는 이것을 단어 임베딩 벡터^{word embedding vector}라고 부릅니다. 그리고 단어들이 모여서 문장이 될텐데요. 따라서 단어 임베딩 벡터가 모여서 문장을 표현하는 행렬이 될 것입니다. 그리고 우리는 문장 행렬을 병렬처리를 위해 덩어리로 묶어야 할테니, 3차원의 텐서가 됩니다. 이것을 그림으로 나타내면 다음과 같습니다.

$N$ 개의 문장을 갖는 텐서 $x$ 는 다음과 같이 나타내질 것입니다.

각 문장은 최대 $\ell$ 개의 단어를 갖고 있을 것이고, 이것은 문장의 길이를 나타냅니다.^[1] 그리고 각 단어는 $d$ 차원의 벡터로 표현될 것입니다.

이와같이 자연어처리를 위한 데이터는 3차원의 텐서로 나타내어집니다. 또 이 데이터의 가장 큰 특징은 문장의 길이에 따라 텐서의 크기가 변할 수 있다는 것입니다. 데이터셋(코퍼스^corpus) 내부의 문장의 길이가 전부 제각각일 것이므로, 어떻게 문장을 선택하여 덩어리로 구성하느냐에 따라서 $\ell$ 의 크기가 바뀌게 됩니다. 즉, 프로그램이 실행되는 와중에 덩어리 텐서의 크기가 가변적이게 되므로, 일반적인 신경망 계층(e.g. 선형 계층)을 활용하여 처리하기 어렵습니다. 따라서 자연어처리의 경우에는 주로 순환 신경망^{recurrent neural networks}을 사용하거나, 트랜스포머^Transformer를 사용하게 됩니다.

컴퓨터비전: 이미지 데이터셋

이번에는 컴퓨터비전^{computer vision}(영상처리) 분야의 텐서의 형태에 대해서 살펴보겠습니다. 주로 이미지 데이터를 다루게 되는데, 먼저 흑백^{gray scale} 이미지부터 보도록 하겠습니다. 다음의 그림은 흑백 이미지 덩어리 텐서를 그림으로 나타낸 것입니다.

흑백 이미지의 각 픽셀은 0부터 255까지의 8 비트^bit(1 바이트^byte) 값으로 표현됩니다. 한 장의 이미지는 세로축 $\times$ 가로축 만큼의 픽셀들로 이루어져 있으며, 이것은 행렬로 표현 가능합니다. 그리고 여러장의 이미지 행렬이 합쳐지면 3차원의 텐서가 됩니다.

다음의 그림은 컬러 이미지의 텐서를 그림으로 나타낸 것입니다. 컬러 픽셀은 RGB 값으로 표현됩니다. RGB 값은 빨강(0~255), 초록(0~255), 파랑(0~255) 값이 모여 $8\times3$ 비트로 표현됩니다. 여기서 각 색깔을 나타내는 값은 채널이라고 부릅니다. 즉, RGB에는 3개의 채널이 존재합니다.

따라서 기존에 한장의 흑백 이미지를 표현하기 위해서는 행렬이 필요했던 반면에, 컬러 이미지는 한장을 표현하기 위해서 3차원의 텐서가 필요합니다. 정확하게는 빨강 값을 나타내는 행렬, 초록 값을 나타내는 행렬, 파랑 값을 나타내는 행렬이 합쳐져서 텐서가 됩니다. 그러므로 이미지 덩어리를 표현하기 위해서는 4차원의 텐서가 필요하고, 이것을 시각화하기는 어려우므로 앞서 그림에서는 $\text{#images}\times$ 라고 표현하였습니다.

테이블 형태의 데이터는 각 열(피쳐^feature)의 값이 굉장히 중요합니다. 예를 들어 첫 번째 열의 값이 실수로 두 번째 열로 옮겨진다면 샘플의 속성이 굉장히 달라지게 됩니다. 하지만 이미지의 경우에는 한 픽셀씩 그림이 평행 이동하더라도 그림의 속성이 바뀌진 않습니다. 따라서 이러한 이미지의 속성을 반영하기 위해서는 마찬가지로 일반적인 계층(e.g. 선형 계층)을 사용하기보단, 합성곱 신경망^{convolution neural network}을 주로 사용합니다.^[2]

[1]: $\ell$ 개보다 적은 단어를 갖고 있는 경우에는 “PAD”라는 특수한 토큰으로 채워질 것입니다.

[2]: 다만 난이도 조절을 위하여, 당분간은 이미지 데이터인 MNIST 라고 할지라도, 가장 기본적인 선형 계층을 사용하도록 합니다.

파이토치 텐서 생성하기

먼저 파이토치를 불러옵니다.

import torch

파이토치 텐서도 다양한 타입의 텐서를 지원합니다.^[3] 다음의 코드는 실수형 Float 텐서를 선언하는 모습입니다.

>>> ft = torch.FloatTensor([[1, 2],
...                         [3, 4]])
>>> ft
tensor([[1., 2.],
        [3., 4.]])

출력 결과를 보면 실수형 값들로 요소들이 채워진 것을 확인할 수 있습니다. 해당 텐서를 실제 행렬로 나타내면 다음과 같습니다.

이처럼 다차원 배열 값(또는 배열 값이 담겨있는 변수)을 넣어 원하는 요소 값을 갖는 텐서를 직접 생성할 수 있습니다. 같은 방법으로 Long 타입과 Byte 타입을 선언할 수 있습니다.

>>> lt = torch.LongTensor([[1, 2],
...                        [3, 4]])
>>> bt = torch.ByteTensor([[1, 0],
...                        [0, 1]])

그리고 임의의 값으로 채워진 원하는 크기의 텐서를 만들고자 한다면 다음과 같이 간단하게 만들 수 있습니다.

>>> x = torch.FloatTensor(3, 2)
>>> x
tensor([[0.0000e+00, 4.6566e-10],
        [0.0000e+00, 4.6566e-10],
        [9.8091e-45, 0.0000e+00]])

[3]: https://pytorch.org/docs/stable/tensors.html

넘파이 호환

파이토치는 넘파이^NumPy와 높은 호환성을 자랑합니다. 실제로 대부분의 함수들은 넘파이와 비슷한 사용법을 가지고 있기도 합니다. 다음과 같이 넘파이를 불러온 후, 넘파이의 배열을 선언하고 출력하면 numpy.ndarray가 할당되어 있는 것을 확인할 수 있습니다.

>>> import numpy as np

>>> x = np.array([[1, 2],
...               [3, 4]]) # Define numpy array.
>>> print(x, type(x))
[[1 2]
 [3 4]] <class 'numpy.ndarray'>

이렇게 선언한 ndarray를 파이토치 텐서로 변환할 수 있습니다.

>>> x = torch.from_numpy(x)
>>> print(x, type(x))
tensor([[1, 2],
        [3, 4]]) <class 'torch.Tensor'>

출력 결과를 보면 파이토치 텐서로 잘 변환된 것을 볼 수 있습니다. 그럼 반대로 파이토치 텐서를 넘파이 ndarray로 변환할 수도 있습니다.

>>> x = x.numpy()
>>> print(x, type(x))
[[1 2]
 [3 4]] <class 'numpy.ndarray'>

텐서 타입 변환

파이토치 텐서의 타입 변환도 굉장히 간단합니다. 단순히 원하는 타입을 함수로 호출하면 됩니다. 다음의 코드는 Float 타입 텐서를 Long 타입 텐서로 변환하는 코드입니다.

>>> ft.long()
tensor([[1, 2],
        [3, 4]])
>>> lt.float()
tensor([[1., 2.],
        [3., 4.]])

텐서 크기 구하기

딥러닝 계산을 수행하다보면 텐서의 크기를 구해야 할 때가 많습니다. 텐서의 크기를 구하는 방법을 알아봅니다. 다음과 같이 $3\times2\times2$ 텐서 x를 선언합니다.

>>> x = torch.FloatTensor([[[1, 2],
...                         [3, 4]],
...                        [[5, 6],
...                         [7, 8]],
...                        [[9, 10],
...                         [11, 12]]])

텐서의 크기를 구하는 방법은 size() 함수를 호출하거나 shape 속성에 접근하면 됩니다. 두 방법의 차이는 없고, size() 함수의 결과 값이 shape 속성에 담겨있다고 보면 됩니다.

>>> print(x.size())
torch.Size([3, 2, 2])
>>> print(x.shape)
torch.Size([3, 2, 2])

이 크기 정보는 배열^list에 담겨있다고 보면 됩니다. 따라서 특정 차원의 크기를 알기 위해서는, shape 속성의 해당 차원 인덱스에 접근하거나 size() 함수의 인자에 원하는 차원의 인덱스를 넣어주면 됩니다.

>>> print(x.size(1))
2
>>> print(x.shape[1])
2

마찬가지로 음수(e.g. -1)를 넣어주면 뒤에서의 순서에 해당합니다.

>>> print(x.size(-1))
2
>>> print(x.shape[-1])
2

그리고 텐서의 차원의 갯수를 알기 위해서는 dim() 함수를 활용합니다. 이것은 shape 속성의 배열 크기와 같습니다.

>>> print(x.dim())
3
>>> print(len(x.size()))
3