AI-Hub 공개 데이터셋을 활용한 한/영 기계번역

이번 포스팅은 AI-Hub에서 공개한 160만 문장쌍의 한국어-영어 문장쌍 코퍼스를 활용한 한/영 기계번역기를 만드는 과정을 공유하고자 합니다. 활용한 전처리 방식에 대해 소개 및 공유하고, Sequence-to-Sequence[1, 2]와 Transformer[3]에 대해서 소개하고 기계번역 학습 결과 성능을 공유하고자 합니다. 또한 강화학습을 활용한 MRT[4]와 Dual Learning에 기반한 DSL[5]을 소개하고, 이를 각 모델에 도입한 결과도 공유하고자 합니다.

이 포스팅의 모든 내용은 패스트캠퍼스의 온라인 자연어생성 강의에 수록되어 있습니다. 해당 강의는 자연어처리 초급 강의에 이어 자연어생성(NLG)를 주로 다루고 있습니다. 특히 아래에서 소개할 기계번역의 사례를 통해, 자연어 생성의 이론과 실습을 총 30시간 이상에 걸쳐 이야기합니다. 해당 강의 또는 이 포스팅과 같은 방법을 통해 우리는 준수한 성능의 기계번역기를 혼자서 개발할 수 있습니다. – 아래의 성능 단락을 참고 바랍니다. 만약 사용자가 적절한 크롤링을 통해 얻은 코퍼스까지 추가한다면 더욱 좋은 기계번역기를 만들 수 있을 것입니다.

깃 저장소(Simple NMT)에 전체 코드가 공개되어 있으니, 필요에 따라 참고하시기 바랍니다. Simple NMT는 Sequence-to-Sequence와 Transformer를 기본 모델로 제공하며, MLE 방식의 학습 이외에도 강화학습을 활용한 MRT 방식, 그리고 Dual Supervised Learning 방식을 통해 학습할 수 있는 코드를 제공합니다. 또한, Beam-search를 지원하여 일반적인 추론방식 대비 더 높은 성능을 얻을 수 있게 합니다.

Preprocessing

Cleaning

다행히 AI-Hub의 데이터들은 이미 잘 정제되어 있는 상태이므로, 굳이 별도의 정제 과정을 거칠 필요가 없습니다. 만약 웹크롤링 또는 영화/드라마 자막을 코퍼스로 삼고자 한다면, 번역에 알맞은 형태로 노이즈를 제거하거나, timestamp를 맞추는 작업 등을 수행해줘야 할 것입니다.

Tokenization

한국어는 말이 길어질 것 같으니, 먼저 영어의 분절(tokenization)에 대해서 먼저 소개합니다.

영어는 굴절어의 성격을 띄는 고립어에 속합니다. (라틴어가 굴절어에 속하지만, 세월이 지나면서 영어는 고립어에 속하게 되었습니다.) 영어의 경우에는 띄어쓰기가 도입된 역사가 훨씬 오래됐기 때문에, 언어 자체가 띄어쓰기와 궁합이 매우 좋습니다. 따라서 띄어쓰기를 따로 교정해줘야 할 필요성은 거의 없습니다. 다만 서로 다른 타입의 캐릭터(character)들 사이에 공백(white-space)을 넣어주는 작업은 필요합니다. 이 작업은 MosesTokenizer를 통해 수행할 수 있습니다.

영어와 달리, 한국어는 교착어에 속합니다. 교착어는 어간에 접사가 붙어 문장 내에서 해당 단어의 의미와 역할이 정해지게 됩니다. 따라서 우리는 하나의 어간에 다양한 접사가 붙을 수 있기 때문에, 단순히 공백을 delimiter로 삼는다면 너무 큰 어휘사전(vocabulary)을 갖게 될 것입니다. 따라서 어간과 접사를 분리함으로써, 어휘사전의 단어 수를 줄이고 단어에 대한 희소성을 감소시킬 수 있습니다.

더욱이 한국어의 경우에는 근대에 띄어쓰기가 도입되었기 때문에, 아직 띄어쓰기와 궁합이 좋지 않습니다. – 여전히 중국어와 일본어에는 띄어쓰기가 존재하지 않습니다. 따라서 우리는 띄어쓰기가 불분명하더라도 의사소통을 하는데 전혀 무리가 없으며, 결과적으로 띄어쓰기가 잘 지켜지지 않는 원인이 됩니다. 즉, 우리가 수집한 데이터셋은 띄어쓰기가 중구난방일 수 있으며, 웹크롤링 등을 통해 수집한 문장이 많을수록 훨씬 더 중구난방이 될 것입니다. 그러므로 우리는 분절(tokenization)을 통해 코퍼스의 띄어쓰기를 정제(normalization)할 수 있습니다.

최신 유행을 따른다면 뒷 단락에서 소개할 서브워드 분절(Subword Segmentation)은 필수적인 요소로 자리잡고 있는데, 이러한 한국어의 언어적 특징을 무시한 채 곧바로 서브워드 분절을 적용한다면, 중구난방 띄어쓰기로 인해 서브워드 분절이 이상적으로 이루어지지 않을 것입니다.

Split into Train/Valid/Test set

이제 이렇게 일차로 분절된 코퍼스를 정해진 비율에 따라 학습/검증/테스트의 3가지 데이터셋으로 분리합니다. AI-Hub에서는 160만 문장쌍으로 이루어진 코퍼스를 제공합니다. 만약 테스트셋을 별도로 마련하지 않고 임의로 구성한다면 아래와 같은 비율도 괜찮은 선택이 될 수 있습니다.

데이터셋	#Lines
학습	140만
검증	19.9만
테스트	0.1만

아쉽게도 저는 처음에 “아무 생각 없이” 일괄적으로 “120만/20만/20만”의 구성을 하는 바람에 학습 데이터가 위의 제안보다 적게 들어갔습니다. 어떻게 보면 위의 구성보다 더 나은 비율 구성 같지만, 20만 문장의 테스트셋은 빔써치(beam-search)와 BLEU측정에서 너무 많은 시간이 소요되어 실제 테스트셋으로 활용하는 것은 사실상 불가능합니다. 따라서 제안된 위의 구성에서 테스트셋이 너무 작은 것이 흠이지만, 어차피 따로 성의있게 잘 구성된 테스트셋이 아니므로 적당히 모델 사이의 성능을 비교하기 위한 용도로 사용하고자 합니다.

Subword Segmentation (Byte Pair Encoding, BPE)

Rich Sennrich 교수에 의해 처음 제안된 서브워드 분절(Subword Segmentation)[6]은 압축 알고리즘인 BPE 알고리즘을 활용합니다. 이제 이 알고리즘은 자연어처리 분야에서 거의 기본이 되었는데요. 중요한 점은 학습셋(training set)을 기준으로 BPE 모델이 학습되어야 한다는 것입니다. 이것도 데이터에 기반하여 통계를 작성하고 이를 바탕으로 분절을 수행하는 것이기 때문에, 학습 데이터만을 보고 분절이 수행되어야 추후에 분절 여부에 따른 정확한 성능을 측정할 수 있습니다.

본래 영어의 경우에도 라틴어의 영향을 받았기 때문에, 각기 다른 의미를 지닌 subword들이 모여 하나의 단어를 이룹니다. 한글의 경우에도 원래 한자의 영향을 받았기 때문에, 각 캐릭터가 의미를 지니고 이것들이 모여 하나의 전체 의미를 지닌 단어를 만들어냅니다.

언어	서브워드	단어
영어	Con(together) + centr(center) + ate(make)	Concentrate
한글	집(모을 집) + 중(가운데 중)	집중

이런 언어의 특성을 반영하여 각 언어별로 별도의 알고리즘을 적용하여 서브워드 분절기를 만드는 대신, BPE 알고리즘을 활용하여 데이터에 기반하여 서브워드 분절을 수행합니다. 다만, 앞선 단락에서 이야기 한 것처럼, 한국어의 경우에는 띄어쓰기가 워낙 중구난방이므로 Mecab을 활용한 분절 이후에 서브워드 분절을 추가로 적용합니다. (Mecab을 활용한 분절은 생략하여도 괜찮습니다.)

Detokenization

텍스트 분류와 같은 task와 달리, 기계번역과 같은 NLG task들은 생성된 문장을 사람이 읽고 이해할 수 있는 형태여야 합니다. 따라서 신경망에 입력되기 좋은 형태로 분절된 생성 문장들을 다시 사람이 읽기 좋은 형태로 만들어주는 작업이 필요합니다. 이러한 작업을 detokenization이라고 부르며, 이는 분절을 수행할 때 약간의 트릭을 추가함으로써 쉽게 해결될 수 있습니다.

영어 원문

There's currently over a thousand TED Talks on the TED website.

tokenization을 수행하고, 기존 띄어쓰기와 구분을 위해 ▁ (U+2581) 삽입

▁There 's ▁currently ▁over ▁a ▁thousand ▁TED ▁Talks ▁on ▁the ▁TED ▁website .

subword segmentation을 수행, 공백 구분 위한 ▁ 삽입

▁▁There ▁'s ▁▁currently ▁▁over ▁▁a ▁▁thous and ▁▁TED ▁▁T al ks ▁▁on ▁▁the ▁▁TED ▁▁we b site ▁. 

whitespace를 제거

▁▁There▁'s▁▁currently▁▁over▁▁a▁▁thousand▁▁TED▁▁Talks▁▁on▁▁the▁▁TED▁▁website▁.

▁▁을 white space로 치환

There▁'s currently over a thousand TED Talks on the TED website▁.

▁를 제거

There's currently over a thousand TED Talks on the TED website.

모델 학습

Simple NMT는 Sequence-to-Sequence 모델과 Transformer 모델을 제공합니다. 또한, 강화학습을 활용한 MRT 방식, Dual Supervised Learning (DSL) 방식을 통해 해당 모델들을 학습할 수 있도록 합니다.

학습 환경

저의 경우에는 MRT와 DSL에서의 적절한 hyper-parameter를 찾기 위해 힘든 과정을 거쳤는데요. 특히, 기계번역의 경우에는 학습의 결과가 1~2일은 소요되기 때문에, 빠르게 결과를 보고 튜닝할 수 없어 어려움이 많았습니다. 처음에는 1080Ti 한 대를 가지고 학습을 진행하다가, 더딘 진행속도에 결국 2080Ti를 2대 더 구입하여 학습을 진행하였습니다. 그 결과 PyTorch에서 제공하는 AMP(Automatic Mixed Precision)[7] 기능의 효과를 체감할 수 있었는데요. 1080Ti의 경우에는 메모리 사용량 개선 뿐, AMP로 인한 속도 개선은 없었던 것에 반해, 2080Ti의 경우에는 메모리 사용량 개선 뿐만 아니라, 속도 개선까지 확인할 수 있었습니다. 결과적으로 2080Ti의 경우에는 같은 조건일 때의 1080Ti에 비해서 2배 이상의 속도 개선이 이루어질 수 있었습니다. 최종적으로는 1대의 1080Ti와 2대의 2080Ti를 갖고 학습을 진행하였습니다.

Sequence-to-Sequence with Attention

Sequence-to-Sequence(Seq2seq)는 이전까지 별다른 연구가 진행되지 못하던 NLP 학계에 큰 파란을 일으키며, NLG의 시대를 연 장본인입니다. 특히, Attention과 함께 시너지를 내며, 순식간에 기계번역을 정복하였습니다. Seq2seq는 크게 3가지 서브모듈로 이루어져 있습니다.

첫 번째로는 인코더입니다. 인코더는 입력 문장을 처음부터 끝까지 받아, bi-directional LSTM을 통해 문장을 하나의 벡터로 압축변환 합니다. 그리고 디코더는 인코더로부터 해당 벡터를 넘겨받아 디코딩을 시작합니다. 디코딩 작업은 <BOS>라는 special token이 첫 번째 입력으로 들어오면 다음 단어를 예측하기위한 출력(hidden state)을 반환합니다. 마지막으로 제너레이터는 이 hidden state를 입력으로 받아 softmax layer를 거쳐 각 단어별 확률 값을 반환합니다.

이를 아래와 같이 Maximum Likelihood Estimation (MLE)를 통해 학습을 진행하게 됩니다.

\[\begin{gathered} \mathcal{D}=\{(x_i, y_i)\}_{i=1}^N \\ \text{where }x_i=\{x_{i,1},\cdots,x_{i,n}\}\text{ and }y_i=\{\text{<BOS>},y_{i,1},\cdots,y_{i,m},\text{<EOS>}\}. \\ \\ \begin{aligned} \mathcal{L}(\theta)&=-\frac{1}{N}\sum_{i=1}^N{ \log{P(y_i|x_i;\theta)} } \\ &=-\frac{1}{N}\sum_{i=1}^N{ \sum_{t=1}^{m+1}{ \log{P(y_{i,t}|x_i,y_{i,<t};\theta)} } } \end{aligned} \\ \\ \hat{\theta}=\underset{\theta\in\Theta}{\text{argmin }}{\mathcal{L}(\theta)} \end{gathered}\]

Transformer

Transformer는 현재 자연어처리의 모든것이라고 해도 과언이 아닙니다. 2017년 처음 발명된 이래로, 자연어 생성 분야 뿐만 아니라 자연어 이해 분야에서도 주도적인 역할을 하고 있으며, 심지어 영상처리(Computer Vision)이나 음성인식(Automatic Speech Recognition, ASR)에서도 두각을 나타냅니다. Simple NMT에서는 Transformer를 제공함으로써 더 나은 기계번역 성능을 쉽게 얻을 수 있도록 합니다. 또한 기존의 original paper에서 제시된 vanilla Transformer 대신에, Pre-Layer-Normalized Transformer[8]를 직접 구현하여 제공합니다.

기존의 Transformer의 경우에는 비록 논문에서 제시된 성능은 매우 높았지만, learning-rate warm-up & decay 방식을 통해 학습을 진행해야 하고, 이는 Adam을 활용함에도 불구하고 또다시 learning-rate 튜닝을 진행해야 하는 어려움을 낳았습니다. 더욱이 이 learning-rate warm-up의 경우에는 hyper-paramter에 매우 취약하여, seq2seq를 이기는 것조차 어려움이 많았습니다. 이에 이러한 어려움을 타파하고자 많은 연구들[9]이 이어졌고, Pre-LN Transformer의 경우에는 learning-rate warm-up 없이 일반적인 Adam을 사용하여도 최적화가 가능하였습니다.

결과적으로 Simple NMT에서도 Transformer는 기존 Seq2seq 대비 더 빠른 학습 속도와, 훨씬 더 높은 기계번역 성능을 얻을 수 있었습니다.

Minimum Risk Training (MRT)

Simple NMT는 강화학습을 활용한 Minimum Risk Training (MRT)[4] 방식을 통해 학습하는 기능을 제공합니다.

Seq2seq와 Transformer와 같은 모델들은 기본적으로 MLE를 통해 학습하게 될 때, teacher-forcing이라는 방법을 사용합니다. Teacher-forcing은 학습할 때에 디코더의 입력에 이전 time-step의 출력 대신 정답을 넣어주어 likelihood를 구하는 것입니다. 하지만 추론의 경우에는 이전 time-step의 출력을 다음 time-step의 디코더의 입력으로 넣어주며, 샘플링 기반의 generation을 하게 됩니다. 따라서 학습과 추론이 다른 방식으로 이루어진다는 단점이 있습니다. 이러한 문제는 auto-regressive 모델 학습에서 발생하는 전형적인 문제입니다.

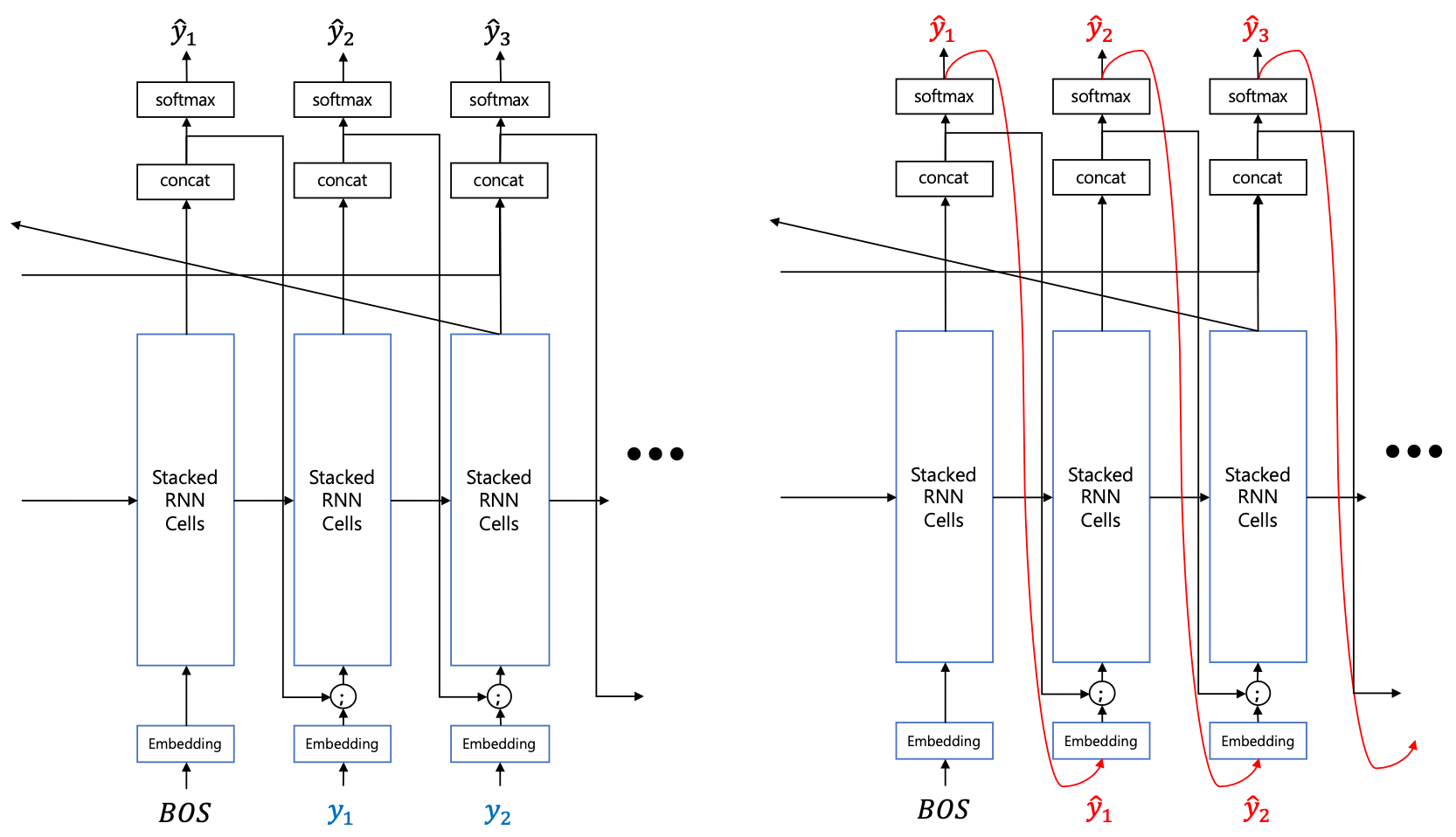
따라서 우리는 비록 teacher-forcing이 훌륭하게 동작하지만, 학습과 추론 방식의 괴리를 줄이면 더욱 잘 동작하지 않을까 기대해볼 수 있습니다. 이러한 이유에서 예전부터 MLE 기반의 teacher-forcing 대신에, 추론에서 사용하는 generation 기반의 방식을 활용하기 위한 연구가 많이 시도되었습니다.

또한 기계번역과 같은 NLG task들은 보통 BLEU나 ROUGE 등의 metric을 통해 결과를 채점하는데, PPL(Cross Entropy)을 최소화 하는 것은 BLEU나 ROUGE를 최대화 하는 것과 다른 결과를 낳을 수 있습니다. 즉, 우리의 목표는 BLEU를 최대화 하는 것이지만 PPL을 최소화 하고 있는 상황이므로, 기계번역의 성능을 극대화 하지 못하고 있을 수 있다는 것입니다. – 여기에는 BLEU가 기계번역의 품질의 꽤 정확하게 반영할 수 있다는 가정이 있습니다.

\[\begin{gathered} \mathcal{D}=\{(x_i,y_i)\}_{i=1}^N \\ \nabla_\theta\mathcal{L}(\theta)=\nabla_\theta\Big( \sum_{i=1}^N{ \log{P(\hat{y}_{i,0}|x_i)\times-\big( \text{reward}(\hat{y}_{i,0},y_i)-\frac{1}{K}\sum_{k=1}^K{ \text{reward}(\hat{y}_{i,k},y_i) } \big)} } \Big), \\ \text{where }\hat{y}_i\sim{P(\cdot|x_i;\theta)}. \\ \\ \theta\leftarrow\theta-\eta\cdot\nabla_\theta\mathcal{L}(\theta) \end{gathered}\]

하지만 MRT의 경우에는 위의 수식에서 볼 수 있듯이, risk(or reward) 함수를 직접 미분할 필요가 없어, BLEU 함수를 통해 최적화를 수행할 수 있습니다. 정리해보면, MRT를 학습이 도입함으로써 우리는 아래와 같은 이점을 얻을 수 있습니다.

샘플링 기반 최적화를 통한 학습과 추론 방식의 괴리 최소화
BLEU 활용을 통한 실제 번역 품질에 대한 최적화

Dual Supervised Learning (DSL)

MRT의 경우에는 뚜렷한 단점도 존재합니다. 우선 샘플링에 기반하여 학습이 진행되므로 훨씬 비효율적입니다. 샘플링에 기반한다는 것은 exploration을 많이 한다는 것이므로, 시간이 많이 소요되는 단점이 있습니다. 또한 risk 자체는 scalar 값이므로, risk를 최소화 하기 위한 정확한 방향은 알 수 없습니다. – 이에 반해 MLE의 경우에는 gradient가 나오므로 loss를 최소화 하기 위한 방향과 크기를 알 수 있습니다.

따라서 MRT와 달리, DSL[5]의 경우에는 MLE의 scheme 안에서 기존의 문제들을 해결하려 합니다. 두 문장 사이의 정보는 동일하다는 번역의 특징을 활용하여, dual learning을 통해 성능을 높이고자 합니다. 기계번역의 경우에는 DSL과 같이 이러한 특징을 활용한 연구들[10, 11]이 많이 이어져왔습니다.

\[\begin{gathered} \mathcal{L}(\theta_{x\rightarrow{y}})=\sum_{i=1}^N{ \Big( \ell\big( f(x^i;\theta_{x\rightarrow{y}}),y^i \big) +\lambda\mathcal{L}_\text{dual}(x^i,y^i;\theta_{x\rightarrow{y}},\theta_{y\rightarrow{x}}) \Big) } \\ \mathcal{L}(\theta_{y\rightarrow{x}})=\sum_{i=1}^N{ \Big( \ell\big( f(y^i;\theta_{y\rightarrow{x}}),x^i \big) +\lambda\mathcal{L}_\text{dual}(x^i,y^i;\theta_{x\rightarrow{y}},\theta_{y\rightarrow{x}}) \Big) } \\ \text{where }\mathcal{L}_\text{dual}(x^i,y^i;\theta_{x\rightarrow{y}},\theta_{y\rightarrow{x}})=\Big\| \big( \log{P(y^i|x^i;\theta_{x\rightarrow{y}})+\log{\hat{P}(x^i)}} \big)-\big( \log{P(x^i|y^i;\theta_{y\rightarrow{x}})+\log{\hat{P}(y^i)}} \big) \Big\|_2^2. \end{gathered}\] \[\nabla_{\theta_{x\rightarrow{y}}}\mathcal{L}_\text{dual}(x^i,y^i;\theta_{x\rightarrow{y}},\theta_{y\rightarrow{x}})=\nabla_{\theta_{x\rightarrow{y}}}\Big\| \big( \log{P(y^i|x^i;\theta_{x\rightarrow{y}})+\log{\hat{P}(x^i)}} \big)-\big( \log{P(x^i|y^i;\theta_{y\rightarrow{x}})+\log{\hat{P}(y^i)}} \big) \Big\|_2^2.\]

위의 수식에서처럼 regularization term의 추가를 통해 auto-regressive 모델 학습에서 생길 수 있는 문제를 해결하고자 합니다.

DSL의 경우에는 MLE 위에서 동작하므로, MRT에 비해 훨씬 효율적인 최적화가 가능합니다. 다만 인코더-디코더 모델과 LM 모델을 각각 2개씩 들고 학습을 진행해야 하기 때문에, 메모리의 한계로 인해 작은 미니배치 사이즈를 사용해야 하는 한계는 존재합니다. (Transformer의 경우에는 gradient accumulation을 활용하므로 실제 파라미터 업데이트에 활용되는 샘플의 숫자는 훨씬 큽니다.)

Summary

아래의 테이블은 각 아키텍처와 알고리즘에 따른 하이퍼파라미터를 정리한 내용입니다. 아쉽게도 MRT의 경우에는 Transformer의 generation이 워낙 메모리를 많이 먹는 탓에 수행할 수 없었습니다. – 캐싱을 없애고 generation의 속도를 낮추면 가능할 수 있습니다. MRT와 DSL은 각각 MLE의 모델들을 pretrained 모델로 활용하며, 상황에 따라 다른 optimizer와 learning rate를 활용합니다.

Hyper-param	Seq2seq (MLE)	Transformer (MLE)	Seq2seq (MRT)	Seq2seq (DSL)	Transformer (DSL)
word_vec_size	512	-	512	512	-
hidden_size	768	768	768	768	768
n_layers	4	4	4	4	4
dropout	.2	-	.2	.2	-
batch_size	320	4096	320	320	4096
n_epochs	30	30	30 + 40	30 + 10	30 + 10
optimizer	Adam	Adam	Adam + SGD	Adam	Adam
learning_rate	1e-3	1e-3	1e-3 $\rightarrow$ 1e-2	1e-3 $\rightarrow$ 1e-2	1e-3 $\rightarrow$ 1e-2
max_grad_norm	1e+8	1e+8	1e+8 $\rightarrow$ 5	1e+8	1e+8

또하나 눈여겨봐야 할 점은 seq2seq와의 형평성을 고려하여 Transformer의 경우에 원래 페이퍼에서 제시한 base model보다 훨씬 작은 모델이라는 것입니다. 저자는 8개의 레이어를 기본 베이스 모델로 삼았는데, 여기서는 4개의 레이어만을 가졌으며 hidden_size의 경우에도 훨씬 작습니다.

Evaluation

실험 데이터는 상기한 AI-Hub의 데이터를 활용하였습니다. 위에서 적은대로 실수로 Train/Valid/Test를 6:2:2로 나눈 바람에 train 데이터가 매우 적습니다. 이에 반해 test 데이터는 20만 문장을 전부 번역하고 BLEU를 측정하기엔 너무 힘들어서 1,000 문장만 다시 선택되었습니다. 즉, 약 19만9천 문장이 버려졌습니다.

set	lang	#lines	#tokens	#characters
train	en	1,200,000	43,700,390	367,477,362
	ko	1,200,000	39,066,127	344,881,403
valid	en	200,000	7,286,230	61,262,147
	ko	200,000	6,516,442	57,518,240
valid-1000	en	1,000	36,307	305,369
	ko	1,000	32,282	285,911
test-1000	en	1,000	35,686	298,993
	ko	1,000	31,720	280,126

전처리 결과, 각 언어별 vocab 크기는 아래와 같습니다.

en	ko
20,525	29,411

Beam Search에 따른 성능

Simple NMT는 Beam-search 기능을 제공합니다. NLG의 경우에는 auto-regressive 속성 때문에, 단순하게 매 time-step마다 argmax를 통해 얻은 결과물은 성능이 떨어지는 경우가 많습니다. 따라서 Beam-search를 통해 우리는 NLG의 성능을 개선할 수 있습니다.

beam_size	enko	koen
1	31.65	28.93
5	32.53	29.67
10	32.48	29.37

위의 테이블과 같이 beam_size에 따라 BLEU 성능이 달라지는 것을 볼 수 있습니다. 기계번역 task의 경우에는 beam_size가 5에서 10 사이가 적당한 것으로 볼 수 있습니다.

아키텍처와 학습 방식에 따른 성능

Transformer의 경우에는 저자가 제안한 모델에 비해 훨씬 작은 모델임에도 불구하고, seq2seq를 압도하는 성능을 보여주고 있습니다. 심지어 Transformer의 MLE 방식은 Seq2seq의 모든 방법들보다 더 높은 성능을 보여줍니다.

MRT와 DSL의 경우에는 MLE보다 높은 성능을 보여주며, 서로간에는 비등비등한 성능을 보입니다. Transformer의 경우에도 DSL을 적용할 경우, MLE보다 더 높은 성능을 얻을 수 있는 것을 알 수 있습니다.

	enko	koen
Sequence-to-Sequence (MLE)	32.53	29.67
Sequence-to-Sequence (MRT)	34.04	31.24
Sequence-to-Sequence (DSL)	33.47	31.00
Transformer (MLE)	34.96	31.84
Transformer (MRT)	-	-
Transformer (DSL)	35.48	32.80

MRT: reward 함수에 따른 성능

MRT의 risk(또는 RL에서의 reward) 함수는 사용자의 필요에 따라 다르게 활용될 수 있습니다. Reward는 클수록 좋고, risk는 작을수록 좋은 값이기 때문에, 기본적으로 BLEU 함수를 활용하여 그 결과값에 -1을 곱해주면 risk로 생각할 수 있습니다. GNMT에서는 단순히 BLEU를 reward 함수로 활용할 경우 agent가 빈틈을 찾아 최적화를 시도하므로, 이를 보완한 Google BLEU (GLEU)를 제안하였습니다.

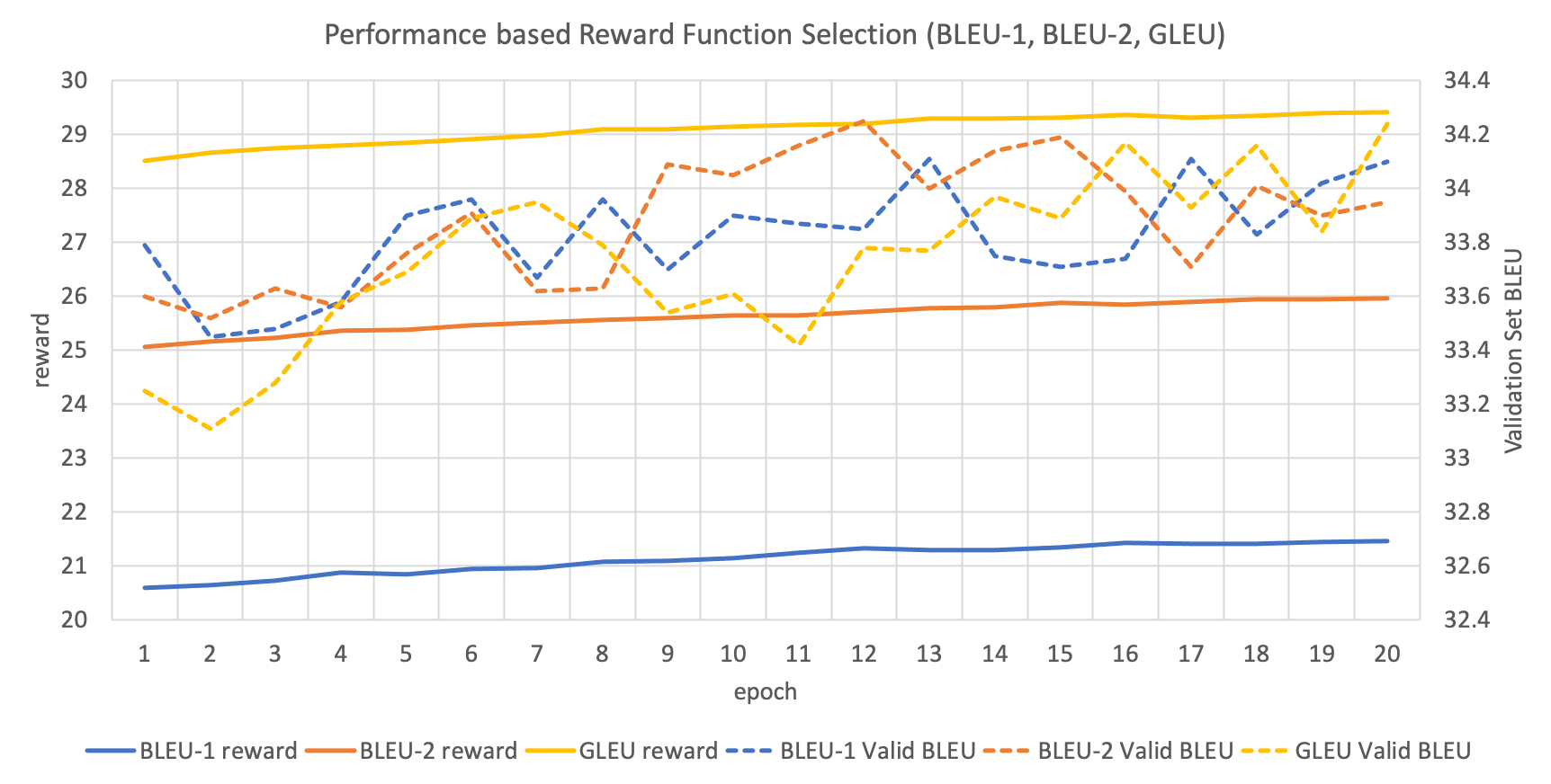
위 그래프는 각 reward 함수에 따른 train과 validation의 성능을 나타냅니다. BLEU-1과 BLUE-2는 각기 다른 smoothing 방식을 나타냅니다. 이 결과에서 주의할 점은 속도의 한계 때문에, train 할 때에는 결과 문장에 detokenization을 한 이후에 BLEU 등을 구하지 못하였고, 분절된 토큰을 그대로 둔 채로 reward 함수를 적용하였습니다. 그리고 validation set에 대해서는 detokenization까지 완료한 이후에 성능을 측정한 것입니다.

결과적으로 위 그래프를 보면 우리는 reward 함수에 대해서 성능이 크게 변하지 않음을 알 수 있습니다.

MRT: reward 함수에서 활용되는 n-gram에 따른 성능

위의 reward 함수를 적용할 때, BLEU와 GLEU 모두 얼마까지의 n-gram을 가지고 채점할지 정해줘야 합니다. 아래의 그래프는 이를 실험한 것입니다. 여기서도 위에 적은 것처럼 training 과정에서 분절되어 있는 토큰들을 기준으로 n-gram을 counting하는 것임을 주의해주세요.

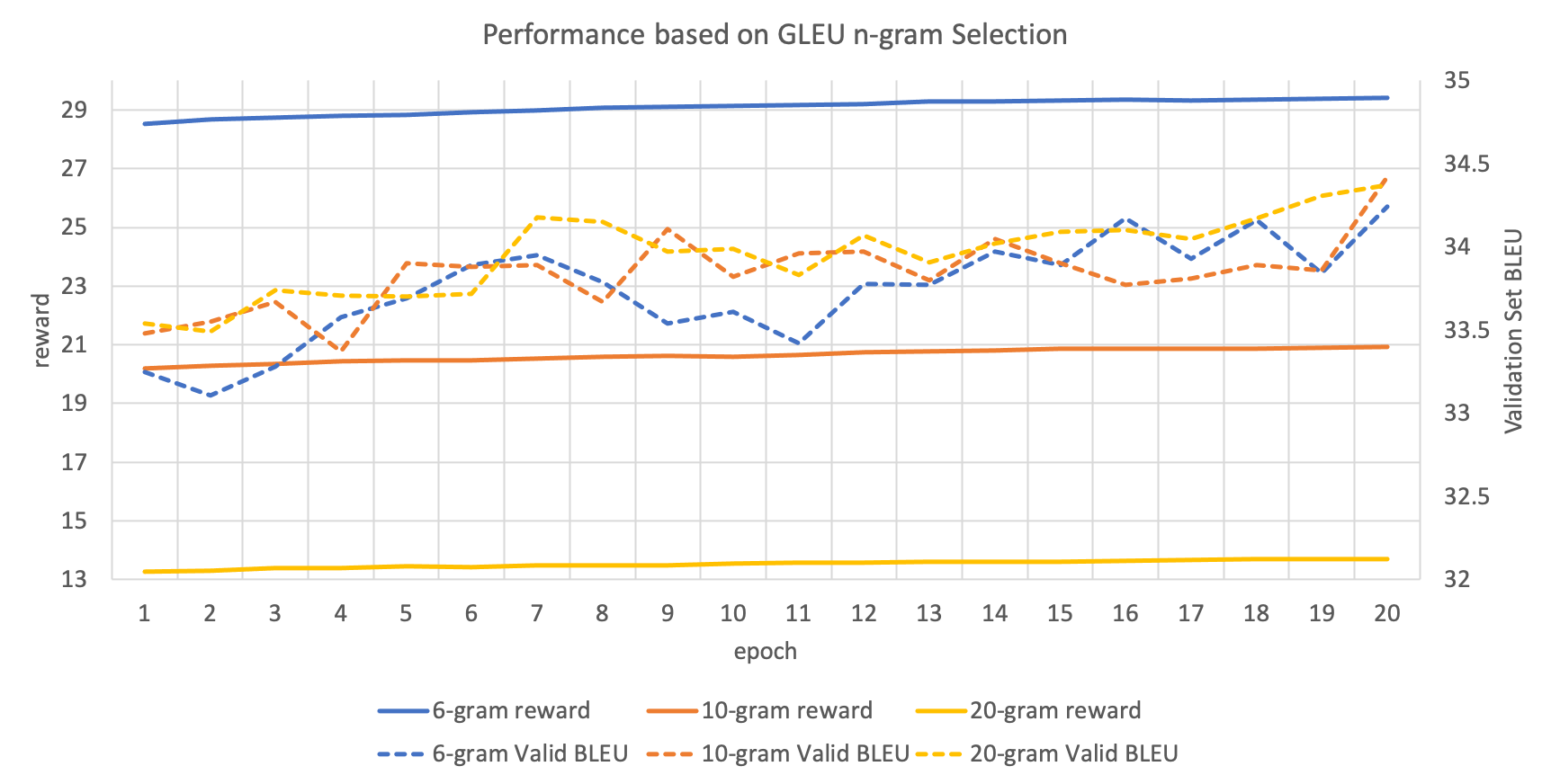
이 경우에도 딱히 어떤 n-gram을 택해야 하는지 명확한 결론을 얻을 수 없었습니다. 하지만 모든 실험 케이스에 대해서 train과 validation의 성능이 올라가는 것을 확인할 수 있습니다.

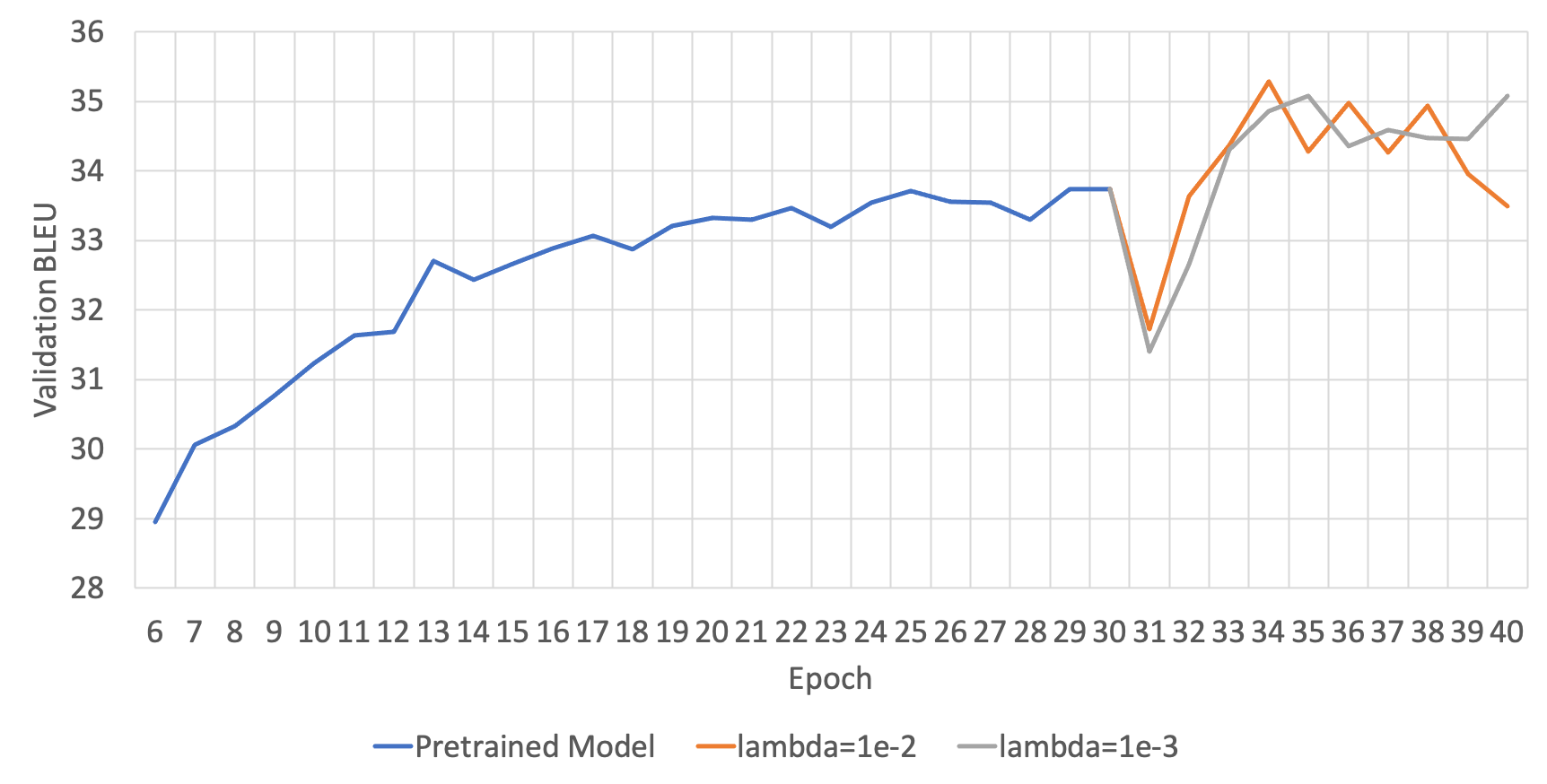
DSL: Lagrangian Multiplier( $\lambda$ )에 따른 성능

DSL은 위의 수식을 보면, regularization term이 추가된 것을 볼 수 있습니다. 이때 그래서 우리는 regularization term의 크기를 조절하여 모델의 generalization에 도움이 되도록 합니다. 그러므로 이 regularization term의 크기를 조절하는 변수(수식에서는 $\lambda$ )가 또 다른 하이퍼파라미터가 됩니다. 아래의 두 그림은 각 번역 방향 별 하이퍼파라미터에 따른 성능을 보여줍니다.

ENKO

KOEN

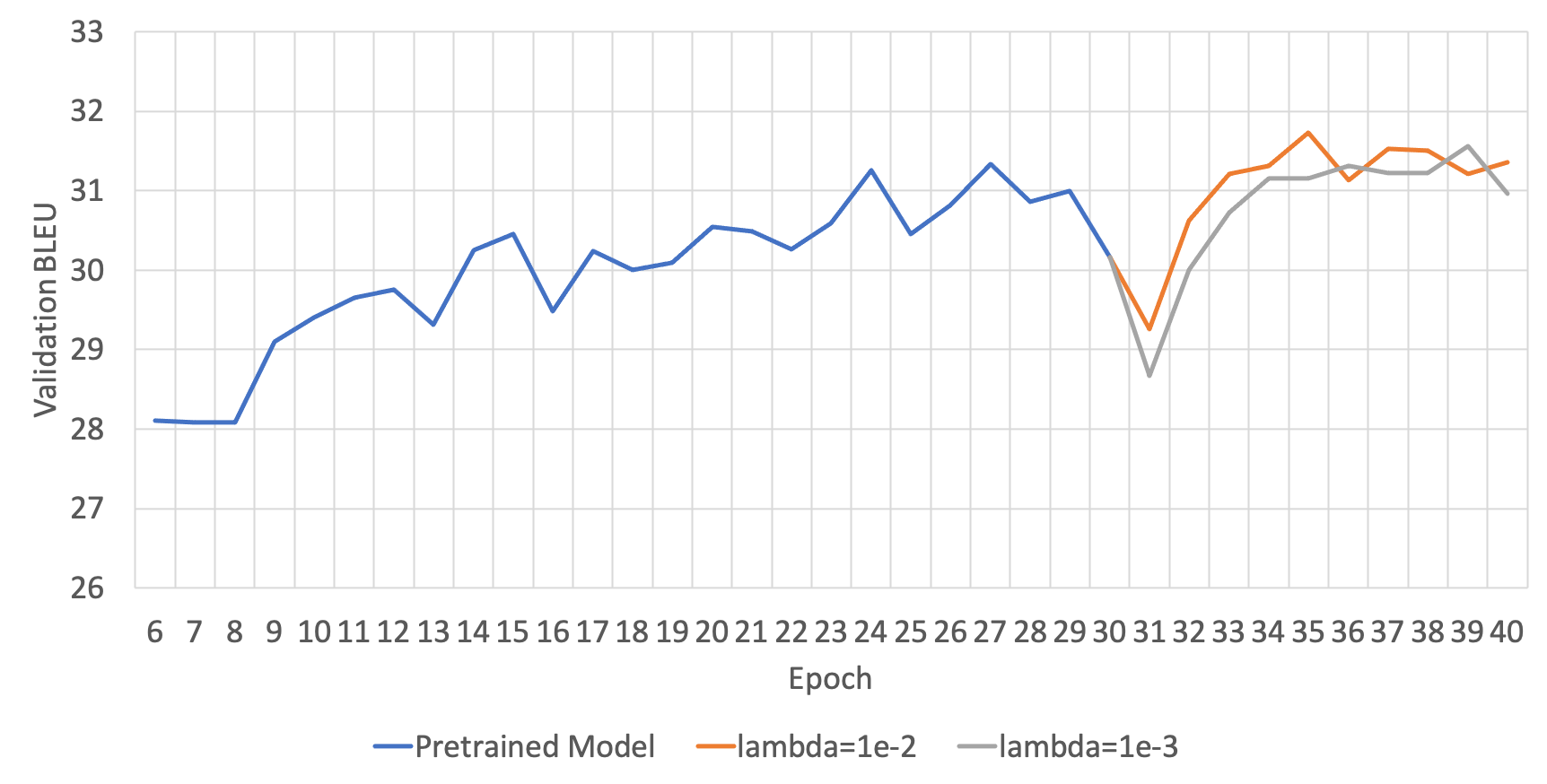
영한(ENKO)의 경우에는 딱히 lambda에 따른 성능 차의가 명확하게 드러나지 않았지만, 한영(KOEN)의 경우에는 1e-2가 더 좋은 성능을 보이는 것을 알 수 있습니다.

실제 결과 비교

일부 테스트셋의 결과를 공유합니다. Transformer가 전체 테스트셋에서는 우위를 지니지만, 일부 문장들에서는 서로 엎치락 뒷치락 하는 것을 볼 수 있습니다. 일부 문장들은 번역 결과로 미루어보건데, REF 문장도 의역이거나 완전한 번역이 아닐 것으로 추측해볼 수 있습니다.

REF	Seq2seq (MLE)	Transformer (MLE)	Seq2seq (MRT)	Seq2seq (DSL)
또한, 이건 미세 혈관을 손상해 당신이 빨간 코를 가지게 할 수 있습니다.	또한 미세한 코를 가질 수 있는 마이너스를 손상시킬 수 있습니다.	또한 그것은 빨간색 코를 가질 수 있는 마이크로바이옴을 손상시킬 수 있습니다.	또한 미세혈관을 손상할 수 있어서 빨간색 코를 가지게 할 수 있습니다.	또한, 당신을 빨간 코로 이끌 수 있는 마이크로셀들을 손상시킬 수 있습니다.
예비신혼부부도 1년이내 혼인 사실이 증명 가능하면 청약할 수 있다.	결혼을 계획하는 부부는 결혼식이 1년 이내인 경우에도 가입할 수 있다.	결혼을 계획하고 있는 부부가 1년 이내에 결혼식이 증명될 수 있는지도 가입할 수 있다.	결혼을 계획하는 부부도 1년 이내 결혼식이 발생할 수 있으면 가입할 수 있다.	결혼을 계획하는 부부는 1년 이내 결혼식이 성사될 경우 가입할 수도 있다.
택배 박스의 빈 곳에 한국 주소도 같이 붙여주시면 감사하겠습니다.	택배 박스의 빈 공간에 한국 주소를 첨부하여 주시면 감사하겠습니다.	택배 박스의 빈 공간에 대한 한국 주소를 첨부해주시면 감사하겠습니다.	택배함의 빈 공간에 한국 주소를 첨부해주시면 감사하겠습니다.	택배 상자의 빈 공간에 한국 주소를 첨부해 주시면 감사하겠습니다.
수백만 가입자가 일상 환경에서 초고속 데이터 전송과 음성통화를 이상 없이 이용하도록 망 안정화와 업그레이드, 커버리지 확대를 지속하는 일은 최우선 과제다.	가입자 수백만 명이 일상 환경에 문제없이 초고속 데이터 전송과 음성 호출을 이용하는 것은 네트워크 안정화, 커버리지 고도화, 커버리지 확대 등이 최우선 과제다.	네트워크 안정화, 업그레이드, 커버리지 확대 등은 수백만 명의 가입자가 고속 데이터 전송과 음성통화를 일상 환경에서 별다른 문제 없이 이용할 수 있는 최우선 순위다.	수백만 명의 가입자가 일상 환경에 문제 없이 초고속 데이터 전송과 음성통화를 이용하는 것이 네트워크 안정화, 업그레이드, 확대 안정성이 최우선이다.	가입자 수백만명이 일상 환경에서 문제없이 고속 데이터 전송과 음성통화를 이용할 수 있도록 네트워크를 안정화하고, 커버리지를 확대·확대하는 것이 최우선 과제다.
단기적으로 시장의 변동성은 지속될 것으로 전망되지만 역사적 관점에서 볼 때 최근 시장의 변동성이 특별히 극심한 것은 아니며 장기적인 시장 펀더멘털 역시 여전히 견고해 보인다.	단기적으로 시장 변동성은 지속될 것으로 전망되지만 역사적 관점에서 보면 최근 시장의 변동성이 특별히 극단적이지 않고 장기간 시장 펀더멘털도 남아 있는 것으로 보인다.	단기적으로는 시장 변동성이 지속될 것으로 전망되지만, 역사적 관점에서 보면 최근 시장 변동성은 특별히 극단적이지 않고 장기적 시장 펀더멘탈도 여전한 것으로 보인다.	단기적으로 시장 변동성이 이어질 것으로 전망되지만 역사적 관점에서 최근 시장의 변동성은 특별히 극적으로 극단적이지 않고 장기적인 시장 펀더멘털도 남아 있는 것으로 보인다.	단기적으로 시장 변동성이 지속될 것으로 전망되지만 역사적 측면에서 보면 최근 시장의 변동성은 특별히 극단적이지 않고 장기적인 시장 근본성도 남아 있는 것으로 보인다.
기존 플라잉 프로브는 제품의 가격이 너무 고가인 데다 ICT와 같은 기존 시험 장비에 비해 시험 시간이 길어서 양산라인에 적용하기 어렵다는 단점이 있다.	기존 비행조사는 제품 가격이 너무 높고 시험시간도 ICT 등 기존 테스트 장비보다 길기 때문에 양산 라인을 적용하기가 어렵다.	기존의 비행용 탐사선은 제품 가격이 너무 비싸고 시험시간이 ICT 등 기존 시험 장비에 비해 길기 때문에 양산선에 적용하기 어렵다.	기존의 비행 탐사선은 제품 가격이 너무 높고, 시험시간이 ICT 등 기존 테스트 장비보다 길기 때문에 양산 라인에 적용하기 어렵다.	기존 플라잉 프로브는 제품 가격이 너무 높고, 시험시간이 ICT 등 기존 시험 장비보다 길어 양산 라인에 적용하기 어렵다.
장우혁의 이번 공연이 성황리에 마무리된 것은 놀랄 만한 일이다.	장우혁의 활약이 성황리에 마무리되었다는 점은 놀라운 일이다.	장우혁의 활약이 성공적으로 마무리 된 것은 놀라운 일이다.	장우혁의 공연이 성공적으로 마무리되었다는 점은 놀라운 일이다.	장우혁의 활약이 성공적으로 마무리되어 놀라움을 금할 수 없다.
문희상 의원은 조문 후 기자들과 만나 “나라가 소용돌이 한복판에 놓였을 때 국가의 큰 어르신 가르침이 그 어느 때보다 아쉬운데 돌아가시게 돼 진심으로 애도를 표한다”고 말했다.	문재인 의원은 조의 끝에 기자들과 만나 “국가가 소용돌이에 빠져 있을 때 큰 고령화를 줄 수 있는 사람이 분실이라는 점에 진심으로 애도를 표한다”고 말했다.	문희상 의원은 조문이 끝난 뒤 기자들과 만나 “국가가 소용돌이 속에 있을 때 위대한 옛 가르침을 줄 수 있는 사람을 잃었다는 것에 대해 진심으로 애도의 뜻을 표한다”고 말했다.	문재혁 의원은 애도한 뒤 기자들과 만나 “소용돌이 한복판이 있을 때 큰 가르침을 줄 수 있는 사람의 손실이라는 것에 진심으로 애도를 표한다”고 말했다.	문희상 의원은 조문 끝에 기자들과 만나 “국가가 소용돌이에 한창일 때 훌륭한 가르침을 줄 수 있는 사람의 상실이라는 애도를 표한다”고 말했다.
한 은행권 관계자는 “기존에는 자체 DSR 기준에 걸려도 심사역이 승인하면 대출이 가능했는데, 관리지표로 본격 도입되면 사실상 대출이 어려워질 것”이라고 전했다.	은행권 관계자는 “예전에는 자체 DSR 기준에 해당돼도 심사팀이 대출을 승인하면 대출을 할 수 있었는데, 경영지표로 도입되면 실질적으로 대출을 받기 어려울 것”이라고 말했다.	은행권 관계자는 “과거 심사팀이 자체 DSR 기준에 해당하더라도 대출을 승인하면 대출을 받을 수 있는데 관리지표로 도입되면 사실상 대출을 받기 어려울 것”이라고 말했다.	은행권 관계자는 “기존에는 자체 DSR 기준에 해당하더라도 심사단이 대출을 승인하면 대출할 수 있었지만 관리지표로 도입하면 사실상 대출을 받기 어려울 것”이라고 말했다.	한 은행 관계자는 “과거에는 자체 DSR 기준에 해당하더라도 심사팀이 대출을 승인하면 대출을 할 수 있었지만 경영지표로 도입되면 실제로는 대출을 받기 어려워진다”고 말했다.
사회적 감사는 업무가 법규나 규정에는 부합하더라도 공평성이나 형평 등 사회적 규범에 맞지 않는다면 이를 개선하도록 권고해 조직에 변화를 유도하는 것이다.	사회적 감사는 법이나 규정을 준수하더라도 정의나 형평성 등 사회적 규범에 부합하지 않으면 업무 윤리 개선을 시키도록 유도하는 등 조직의 변화를 유도하는 것이다.	사회감사에서는 법이나 규정을 준수하더라도 정당이나 형평 등 사회규범에 맞지 않으면 업무 윤리가 향상될 수 있도록 독려해 조직의 변화를 유도한다.	사회적 감사는 법이나 규정을 준수하더라도 정의나 형평성 등 사회적 규범을 충족하지 않으면 업무 윤리 개선을 유도해 조직의 변화를 격려하고 있다.	사회적 감사는 법이나 규정을 준수하더라도 정의나 형평 등 사회적 규범에 부합하지 않을 경우 업무 윤리 개선을 유도해 조직의 변화를 유도하도록 유도한다.
마찰이 있더라도 국익 차원에서 인터넷 역차별 해소 정책을 강력하게 추진해야 한다는 목소리가 힘을 얻기 시작했다.	마찰이 일어나더라도 인터넷 역차별 정책의 해법을 구현하는 목소리가 국익을 향한 힘을 얻기 시작했다.	마찰이 발생해도 인터넷 역차별 정책의 해법을 시행하자는 목소리가 국익을 위해 힘을 얻기 시작한 것이다.	마찰이 발생하더라도 인터넷 역차별 정책의 해법을 구현하는 목소리가 국익을 위해 힘을 얻기 시작했다.	마찰이 발생하더라도 인터넷 역차별 정책의 해법을 구현해야 한다는 목소리가 국민적 관심에 힘을 받기 시작했다.
오비맥주가 주요 맥주 제품의 가격을 인상키로 하면서 하이트진로와 롯데주류 등도 조만간 맥주 가격을 올릴 가능성이 높아졌다.	오비맥주가 각종 맥주 상품 가격을 올리기로 결정한 만큼 하이트진로와 롯데주류도 가까운 시일 내에 맥주 가격을 인상할 가능성이 높다.	오비맥주가 다양한 맥주 제품 가격 인상 결정을 내린 만큼 하이트진로와 롯데주류도 가까운 장래에 맥주 가격을 인상할 가능성이 높다.	오비맥주가 다양한 맥주 상품의 가격을 올리기로 결정하면서 하이트진로와 롯데주류도 가까운 미래에 맥주 가격을 인상할 가능성이 높다.	오비맥주가 다양한 맥주 상품의 가격 인상을 결정한 만큼 하이트진로와 롯데주류도 가까운 시일 내에 맥주 가격을 인상할 가능성이 높다.
이 사고로 통학차량에 타고 있던 학생 7명(남3, 여4) 중 고교생 3명과 여중생 1명이 다쳐 인근 병원으로 옮겨쳐 치료를 받고 있다.	이 사고로 통근차량에 타고 있던 학생 7명 가운데 고등학생 3명과 여중생 1명이 부상을 입고 인근 병원으로 옮겨져 치료를 받고 있다.	통학 차량에 타고 있던 학생 7명 중 고등학생 3명과 여중생 1명이 부상을 입고 인근 병원으로 옮겨져 치료를 받고 있다.	이 사고로 통학차량에 타고 있던 학생 7명 중고생 3명과 여중생 1명이 다쳐 인근 병원으로 옮겨져 치료를 받고 있다.	통학차량에 타고 있던 학생 7명 가운데 고등학생 3명과 여중생 1명이 다쳐 인근 병원으로 옮겨져 치료를 받고 있다.
반경 1km 내에 용현초, 신광초, 신흥여중 등 다수의 교육시설이 위치해 있고 홈플러스와 현대 유비스 병원 등이 도보 5분 거리 내에 위치해있다.	1㎞ 이내에는 용인초등학교, 신광초등학교, 신흥여중 등 수많은 교육시설이 있으며, 걸어서 5분 거리에 홈플러스, 현대위비병원 등이 있다.	1km 이내에는 용현초등학교, 신왕초, 신흥여자중학교 등 수많은 교육시설이 있으며 도보 5분 거리에 홈플러스와 현대 유비에스 병원이 있다.	1㎞ 안에는 용현초등학교, 신광초등학교, 신흥여학교 등 수많은 교육시설이 있으며, 5분 도보 거리에는 홈플러스와 현대유비병원이 있다.	1km 이내에는 용현초등학교, 신왕초, 신흥여중 등 수많은 교육시설이 있으며 도보 5분 거리에 홈플러스와 현대유비병원이 있다.

Conclusion

이번 포스팅에서는 패스트캠퍼스의 자연어 생성 클래스의 기계번역 실습을 자세히 다뤄 보았습니다. 실제로 MRT와 DSL의 경우에는 MLE 방식보다 더 좋은 성능을 이끌어 낼 수 있음을 확인할 수 있었습니다. 또한 지금의 자연어처리 학계를 지배하고 있는 Transformer의 경우에는, Seq2seq의 어떠한 최적화 방식보다도 더 좋은 성능을 거둘 수 있었습니다. 이를 통해 우리는 Transformer의 대단함을 다시한번 느낄 수 있습니다.

사실 자연어 생성 클래스는 기존의 다른 강의들에 비해서 훨씬 난이도가 높은 것이 사실입니다. 특히, MRT를 다루기 시작하면서부터 수식의 빈도가 급격하게 증가하는데요. 예전 오프라인 강의를 진행 할때도 이 부분부터 수강생 분들도 힘들어하는 것을 느낄 수 있었습니다. 제 개인적인 경험에 비춰 보면 MRT나 DSL을 제대로 구현하기 위해서는 수식을 정확하게 이해하는 것이 중요했는데요. 수식을 정확하게 이해하고 이를 코드로 옮기는 과정에서 한단계 더 성장할 수 있었습니다. 그래서 저는 수강생 분들이 MRT나 DSL을 배우셨으면 하는 마음에서도 이 내용을 강의에 넣었지만, 수식을 이해하고 이를 코드로 옮기는 과정을 체득하셨으면 하는 바램이 더 큽니다. 꼭 제 강의를 수강하시는 분들이 아니더라도, 이 포스팅과 Simple NMT를 참고하여 수식을 코드로 옮기는 과정을 체득할 수 있으면 좋겠습니다.

References

Back-Translation Review

이번 포스팅은 Neural Machine Translation (NMT)에서 널리 사랑받고 있는 Back-Translation[1] (이하 BT)에 대해서 좀 더 이해해보는 시간을 가지려 합니다. 기존에 제안된 BT에 대해서 살펴보고, 기본 BT의 한계를 극복하기 위해 제안된 여러가지 방법들을 여러가지 관점(실험 + 수식)에서 이해해보고자 합니다.

Leverage with Monolingual Corpus

NMT는 2014년 Sequence-to-Sequence의 발명 이후로 자연어생성(NLG) 분야와 함께 큰 발전을 이루어왔습니다. 특히 제가 보았을 때, 2017년 Transformer의 발명 덕분인지, 2018년에 거의 연구의 정점을 찍은 것으로 보입니다. 즉, 구성 요소들이 잘 갖춰진 문장(e.g. 뉴스기사)들에 대해서는 이미 사람의 수준을 넘어섰다고 할 정도의 성능에 이르렀습니다.

하지만 NMT 개발을 위해서는 두 쌍의 언어가 문장 수준에서 mapping되어 있는 parallel corpus가 필수적으로 필요하고, 이는 여전히 low-resource 상황에서의 NMT에서 큰 장벽이 되고 있습니다. 예를 들어, 한국어-영어 번역은 매우 잘 연구/개발되어 있지만, 한국어-태국어와 같은 번역은 이에 반해 훨씬 미비한 상황입니다. 더욱이 인터넷 등에서 무한대로 모을 수 있는 unlabled corpus에 반해, parallel corpus는 매우 수집이 어렵고 비싸기 때문에, 한국어-영어 번역에서도 여전히 parallel corpus 수집에 대한 목마름은 항상 남아있습니다.

따라서 예전부터 단방향 코퍼스(monolingual corpus)를 활용하여 번역기의 성능을 높이고자 하는 시도들은 매우 많았고, 개인적으로도 굉장히 좋아하는 주제라고 생각합니다. – 기계번역의 꽃이랄까요. Language Model Ensemble[2]에서부터 Dual Learning[3, 4]에 이르기까지 정말 많은 연구들이 있었고, 모두 parallel corpus만을 활용한 것보다 더 나은 성능을 제공할 수 있었습니다. 하지만 BT는 굉장히 이른 시기에 제안되었음에도 불구하고, 간단한 방법으로 비교적 훌륭한 결과물을 제공하기 때문에 위의 여러가지 방법들 중에서도 가장 사랑받는 방법 중에 하나였습니다. 이 포스팅에서는 Back-Translation에 대해서 살펴보고, 여러가지 관점에서 살펴보고자 합니다.

Back-Translation

Back-Translation은 에딘버러 대학의 리코 센리치 교수가 제안한 방법으로, 센리치 교수님은 BPE를 통한 subword segmentation을 제안[5]한 분으로도 유명합니다. Parallel corpus의 부족으로 인해 겪는 가장 기본적인 문제중에 하나는, 디코더인 타깃 언어의 언어모델(Language Model, LM)의 성능 저하를 생각해볼 수 있습니다. 즉, 다량의 monlingual corpus를 수집하여 풍부한 표현을 학습할 수 있는 언어모델에 비해, parallel corpus만을 활용한 경우에는 훨씬 빈약한 표현만을 배울 수 밖에 없습니다. 따라서, 소스 언어 문장으로부터 타깃 언어 문장으로 가는 translation model(TM)의 성능 자체도 문제가 될테지만, 번역에 필요한 정보를 바탕으로 완성된 문장을 만들어내는 능력도 부족할 것 입니다.

이때, TM의 성능 저하는 parallel corpus의 부족과 직접적으로 연관이 있지만, LM의 성능 저하는 monolingual corpus를 통해 개선을 꾀해볼 수 있을 것 같습니다. 하지만 예전 Statistical Machine Translation (SMT)의 경우에는 보통 TM과 LM이 명시적으로 따로 존재하였기 때문에 monolingual corpus를 통한 LM의 성능 개선을 쉽게 시도할 수 있었지만, NMT에선 end-to-end 모델로 이루어져 있으므로 LM이 명시적으로 분리되어 있지 않아 어려움이 있습니다. BT는 이러한 상황에서 디코더의 언어모델의 성능을 올리기 위한 (+ 추가적으로 TM의 성능 개선도 약간 기대할 수 있는) 방법을 제안합니다.

보통 번역기를 개발할 경우, 한 쌍의 번역 모델이 자연스럽게 나오게 됩니다. 왜냐하면 우리는 parallel corpus를 통해 번역기를 개발하므로, 두 방향의 번역기를 학습할 수 있기 때문입니다. 이때 Back-Translation이라는 이름에서 볼 수 있듯이, BT는 반대쪽 모델을 타깃 모델을 개선하는데 활용합니다.

예를 들어 아래와 같이 parallel corpus $\mathcal{B}$ 와 monolingual corpus $\mathcal{M}$ 을 수집한 상황을 생각해볼 수 있습니다.

\[\begin{gathered} \mathcal{B}=\{(x_n, y_n)\}_{n=1}^N \\ \mathcal{M}=\{y_s\}_{s=1}^S \end{gathered}\]

그럼 자연스럽게 우리는 일단은 $\mathcal{B}$ 를 활용하여 두 개의 모델을 얻을 수 있습니다.

\[\begin{aligned} \hat{\theta}_{x\rightarrow{y}}&=\underset{\theta\in\Theta}{\text{argmax}}\sum_{n=1}^N{\log{P(y_n|x_n;\theta_{x\rightarrow{y}})}} \\ &=\underset{\theta\in\Theta}{\text{argmin}}\sum_{n=1}^N{\ell\big(f(x_n;\theta_{x\rightarrow{y}}),y_n\big)} \\ \hat{\theta}_{y\rightarrow{x}}&=\underset{\theta\in\Theta}{\text{argmax}}\sum_{n=1}^N{\log{P(x_n|y_n;\theta_{y\rightarrow{x}})}} \\ &=\underset{\theta\in\Theta}{\text{argmin}}\sum_{n=1}^N{\ell\big(f(y_n;\theta_{y\rightarrow{x}}),x_n\big)} \\ \end{aligned}\]

이때, 우리는 $\hat{\theta}_{y\rightarrow{x}}$ 를 통해서 $\mathcal{M}$ 데이터셋에 대한 추론 결과를 얻어, pseudo(or synthetic) corpus를 만들 수 있습니다. 즉, 반대쪽 모델에 monolingual corpus를 집어넣어 $\hat{x}$ 을 구할 수 있습니다.

\[\begin{gathered} \tilde{\mathcal{M}}=\{(\hat{x}_s,y_s)\}_{s=1}^S, \\ \text{where }\hat{x}_s=\underset{x\in\mathcal{X}}{\text{argmax}}\log{P(x|y_s;\theta_{y\rightarrow{x}})}. \end{gathered}\]

이제 그럼 우리는 새롭게 얻은 $\mathcal{M}$ 을 포함하여 $\mathcal{B}$ 와 함께 다시 $\theta_{x\rightarrow}$ 를 학습하면 더 나은 성능의 파라미터를 얻을 수 있다는 것이 BT입니다. 당연히 이것은 반대쪽 모델에도 똑같이 적용 가능할 것 입니다.

\[\hat{\theta}_{x\rightarrow{y}}=\underset{\theta\in\Theta}{\text{argmax}}\bigg( \sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }+\sum_{s=1}^S{ \log{P(y_s|\hat{x}_s;\theta_{x\rightarrow{y}})} } \bigg)\]

이 방법의 핵심은 pseudo sentence가 인코더에 들어가고, 실제 문장이 디코더에 들어가는 것입니다. 이에따라 인코더는 비록 큰 도움을 못받더라도, 디코더는 어쨌든 주어진 인코더의 결과값에 대해서 풍부한 언어모델 디코딩 능력을 학습할 것으로 예상할 수 있습니다.

실험 결과 및 한계

아래와 같이 BT는 굉장히 간단한 구현 방법에 비해 준수한 성능 개선 효과를 보여줍니다.

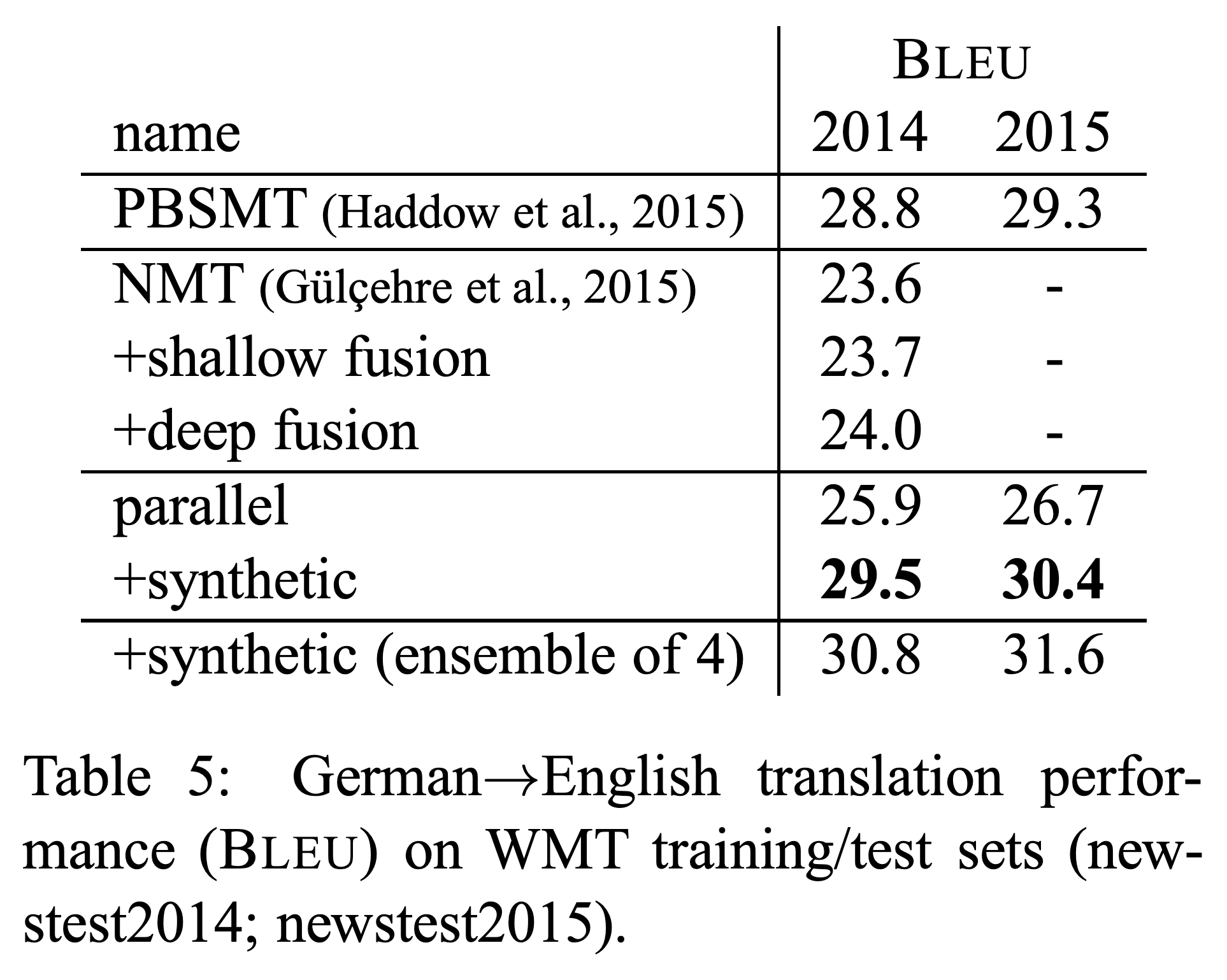
결과 테이블

그런데 중요한 점은 pseudo corpus의 양이 너무 많아서는 안된다는 것입니다. 비록 우리는 무한대에 가까운 monolingual corpus를 얻어 pseudo corpus를 만들어낼 수 있겠지만, 만약 그럴경우 pseudo corpus가 기존 parallel corpus를 압도해버릴 수 있습니다. Pseudo corpus의 경우에는 인코더에 들어갈 $\hat{x}$ 이 실제 정답과는 일부 다를 수 있기 때문이고, 더욱이 $\theta_{y\rightarrow{x}}$ 에 의해 bias가 생겨있는 상태일 것이므로, 너무 많은 양의 pseudo corpus를 활용할 경우 $\theta_{x\rightarrow{y}}$ 가 잘못된 bias를 학습할 경우도 생각해볼 수 있습니다. [6] 따라서 우리는 제한된 양의 $\mathcal{M}$ 만 활용할 수 있으며, 이는 또 하나의 하이퍼파라미터를 추가시킵니다. 그리고 이 하이퍼파라미터는 보통 기존 parallel corpus의 2~3배 정도가 적당하다고 알려져 있습니다.

Noise 추가를 통한 Back-Translation 개선

실제 모든 $\mathcal{M}$ 을 활용하지 못하고 제한된 양을 활용할 수 밖에 없기 때문에, 이 제한된 양을 좀 더 늘릴수 없을지 또 다른 연구들이 이어졌습니다. [7]에서는 pseudo corpus를 생성할 때, noise를 섞으면 BT의 성능이 더 향상되는 것을 확인하였습니다. 예를 들어 generation을 하는 과정에서 argmax(or greedy)를 통해 번역 문장을 생성하는 것보다, random sampling을 통해 random noise를 섞어주거나 beam seach 과정에서 약간의 noise를 섞어주는 것이 기존 BT보다 더 나은 성능을 제공한다는 것입니다.

결과 테이블

이는 인코더에서 $\hat{x}$ 를 학습할 때, 기존 $\theta_{y\rightarrow{x}}$ 의 bias를 학습하는 것을 방해하는 일종의 regularization 역할로도 생각해볼 수 있습니다.

Tagged Back-Translation

여기서 한 발 더 나아가 더 쉬운 방법을 통해 더 높은 성능을 제공하는 방법도 제안되었습니다. [6]에서는 인코더에서의 잘못된 bias 학습으로 인해 번역기 전체 성능이 하락되는 것을 막기 위해, pseudo corpus에 tag를 붙인 상태로 학습하는 것을 제안하였습니다. 좀 더 정확히 말하면 인코더에 입력으로 들어가는 소스 언어의 pseudo sentence의 맨 앞에 pseudo corpus라는 tag를 넣어주어, 네트워크가 pseudo corpus에 대해서는 다르게 행동하여, 실제 테스트 환경에서는 잘못 학습된 bias로 인해 번역 성능이 낮아지는 것을 막고자 하였습니다.

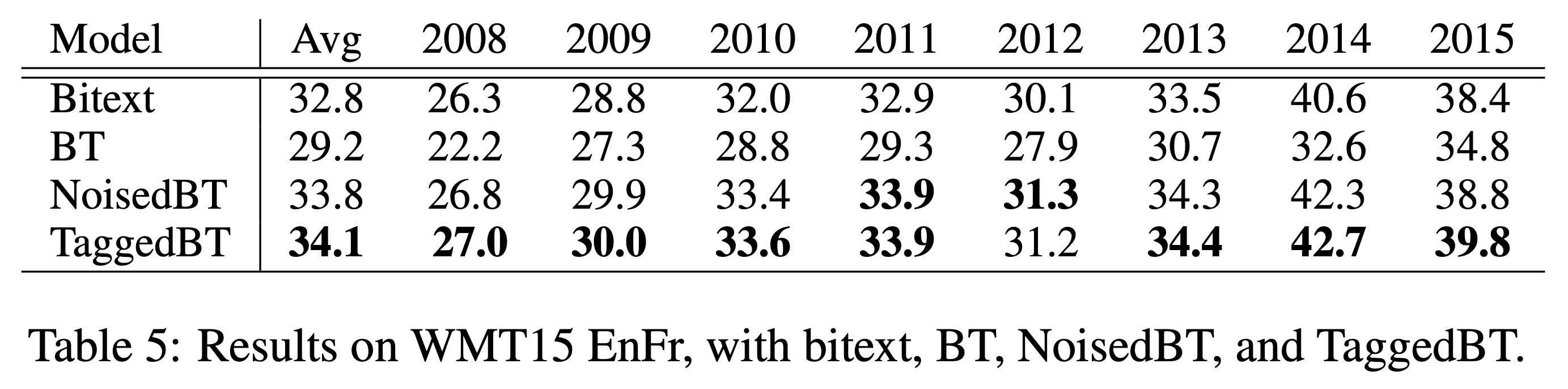
결과 테이블

이 결과 기존 BT 뿐만 아니라, Noise added BT에 비해서도 더 높은 성능 향상을 이끌어냈으며, 심지어 기존 방법에 비해 더 많은 monolingual corpus를 활용 하였을 때도 성능의 저하가 이루어지지 않는 것을 확인하였습니다. 이것은 전체 monolingual corpus를 활용할 수 없어 아쉬움이 남던 BT의 단점을 획기적으로 개선한 것이라고 볼 수 있을 것입니다.

위에서 언급하였듯이, 우리는 tag를 pseudo sentence의 맨 앞에 달아 인코더에 넣어줌으로써, 아마도 인코더는 pseudo corpus를 처리하기 위한 별도의 mode에 들어갈 것이고, 이는 잘못된 bias를 학습하는 것을 방지하여 기존의 parallel corpus 학습에 지장을 주지 않도록 하지 않을까 예상해볼 수 있습니다.

실제 Back-Translation은 효과가 있을까?

이처럼 BT를 활용한 방법들은 간단하면서도 높은 성능을 제공하는 효율성으로 널리 사랑받고 있습니다. 이때, [8]에서는 실제로 BT가 겉으로 보이는 성능 만큼이나 실제로도 번역기의 성능을 개선하는데 도움이 되는지 분석해 보았습니다. 이를 위해 이 논문에서는 아래의 3가지 질문에 대해서 BT에 실제로 어떻게 동작하는지 좀 더 검증해보고자 하였습니다. – 원문 발췌

Q1. Do NMT systems trained on large backtranslated data capture some of the characteristics of human-produced translations, i.e., translationese?
Q2. Does a tag for back-translations really help differentiate translationese from original texts?
Q3. Are NMT systems trained on back-translation for low-resource conditions as sensitive to translationese as in high-resource conditions?

저자는 기존의 논문들에서 사용한 테스트셋(e.g. WMT)의 입력들이 자연스러운 원문장이라기보단 상대적으로 어색한 원문장에 대한 번역문(translationese)들을 포함하고 있으며, BT 방법들이 이러한 테스트셋에서 좋은 성능을 거둘 수 있었던 것은 실제 번역성능이 올랐다기보단 translationese들을 잘 번역했기 때문이라고 주장했습니다. Pseudo sentence $\hat{x}$ 를 인코더에 넣어 학습시키는 것은 bias가 포함되어 있기 때문에, translationese를 잘 번역하도록 할 뿐 실제 원문(본문에서는 original text라고 표현)에 대한 번역 성능은 검증이 필요하다는 것입니다. 이를 위해서 저자는 아래와 같이 기존 각 연도별 WMT 테스트셋에서 original text와 translationese를 구분해서 BT와 Tagged BT의 성능을 각각 검증해보았습니다.

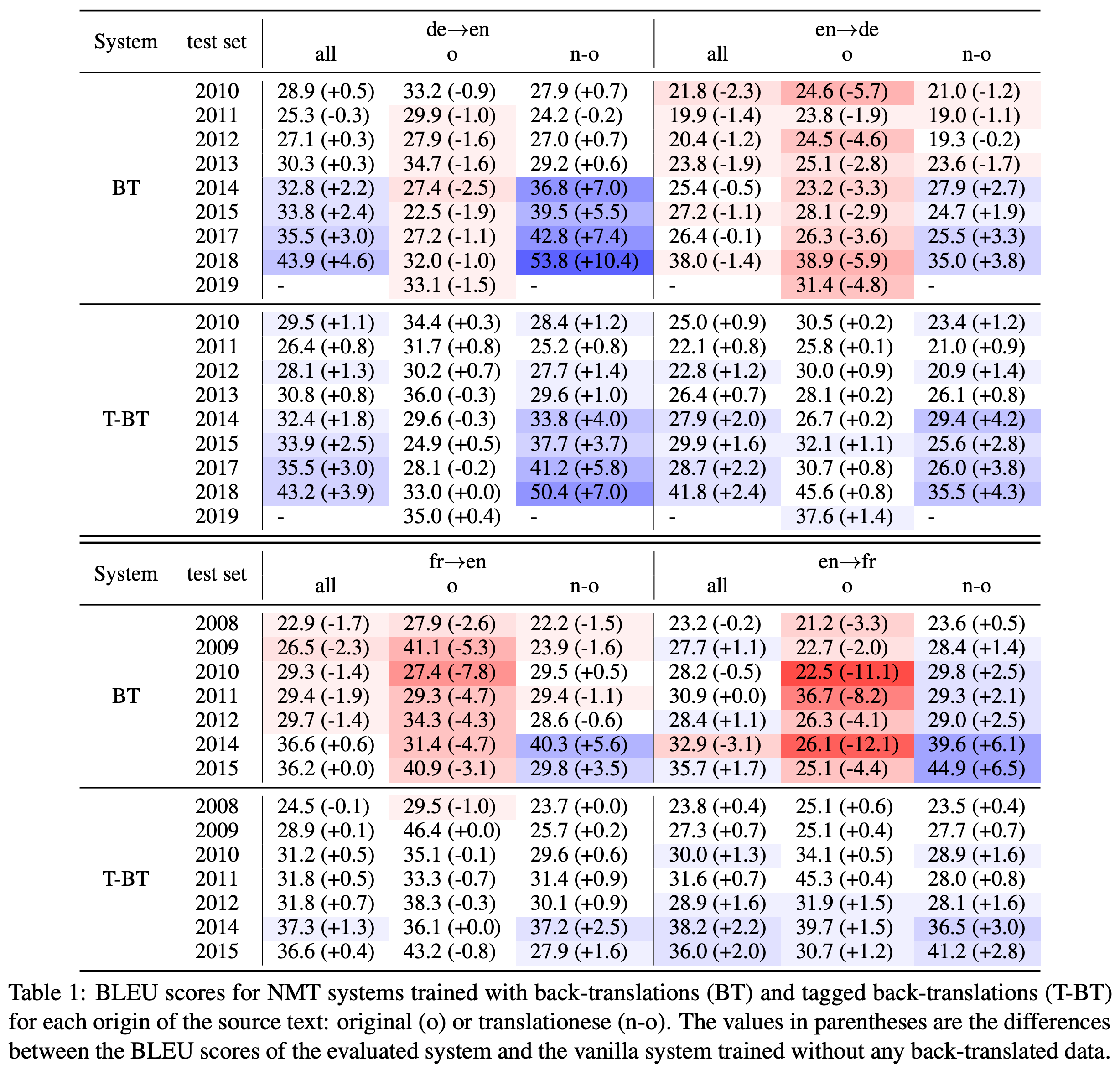
결과 테이블

그 결과 재미있게도 vanilla BT의 경우에는 translationese가 입력으로 주어졌을 때의 성능 향상만 있었을 뿐, original text에 대해서는 오히려 성능이 하락하는 것을 알 수 있습니다. 특히 translationese에 대한 성능 개선이 두드러지는 바람에, 둘이 섞인 전체 테스트셋에서는 오히려 Tagged BT에 비해 성능 향상이 더 큰 것처럼 착시 현상을 일으키기까지 합니다. 이에 반해 Tagged BT의 경우에는 translationese 뿐만 아니라, original text에서도 미미하지만 성능 개선이 있었음을 확인할 수 있습니다.

결국 BT로 인한 성능 향상의 대부분은 번역문과 같은 translationese를 입력으로 받았을 때 일어난 것으로 해석할 수 있습니다. 이것은 물론 실망스러운 결과일 수 있지만, 그렇다고 해서 실제 deploy환경에서 translationese와 같은 입력들이 전혀 없을 것은 아니기 때문에, 전혀 쓸모없는 성능 개선이라고는 볼 수 없을 것입니다.

물론 아래와 같이 low-resource 환경에서의 번역일 때는 BT와 Tagged BT 모두 번역 성능 개선에 매우 큰 도움을 주는 것을 확인할 수 있습니다.

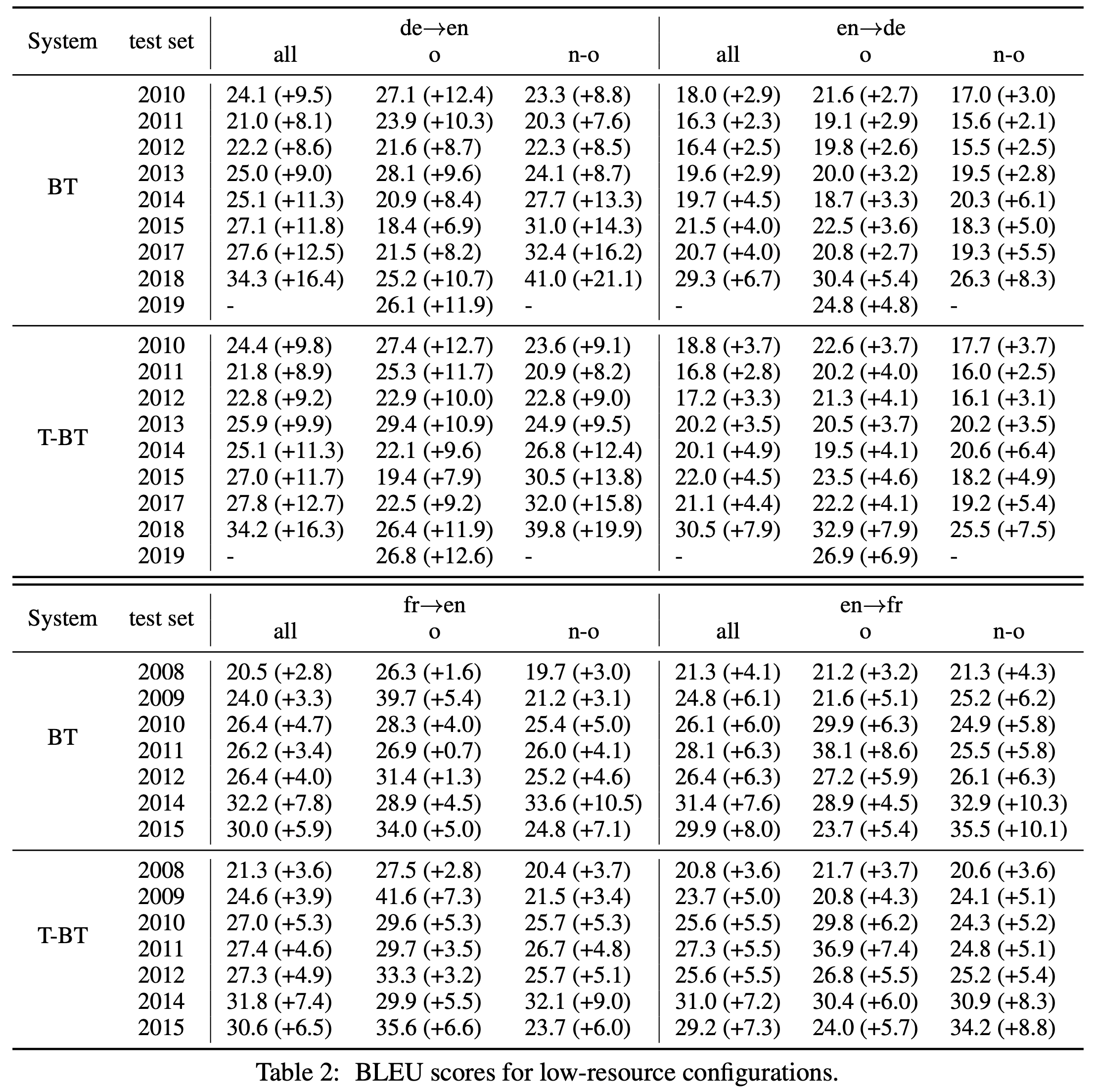
결과 테이블

여기에서도 Tagged BT가 기존 BT보다 original text에서 더 나은 성능 개선 폭을 보이는 것을 확인할 수 있습니다.

Back-Translation 수식으로 풀어보기

사실 BT는 부족한 코퍼스로 인한 디코더 언어모델의 성능개선이라는 미명아래, 직관적인 설명에 의존해서 제안되었습니다. [9]에서는 여기에 수식으로 BT를 설명하기도 하였습니다.

\[\begin{gathered} \mathcal{B}=\{(x_n, y_n)\}_{n=1}^N \\ \mathcal{M}=\{y_s\}_{s=1}^S \end{gathered}\]

아까와 같이 parallel corpus와 monolingual corpus가 수집되었다고 할 때, importance sampling을 통해 아래와 같이 수식을 전개할 수 있을 것입니다.

\[\begin{aligned} \log{P(y)}&=\log{\sum_{x\in\mathcal{X}}{ P(x,y) }} \\ &=\log{\sum_{x\in\mathcal{X}}{ P(y|x)P(x) }} \\ &=\log{\sum_{x\in\mathcal{X}}{ \frac{P(y|x)P(x)}{P(x|y)}P(y|x) }} \end{aligned}\]

그리고 Jensen’s Inequality를 활용하여 부등식을 완성할 수 있습니다. – VAE[10]의 전개와 매우 비슷합니다.

\[\begin{aligned} \log{P(y)}&=\log{\sum_{x\in\mathcal{X}}{ \frac{P(y|x)P(x)}{P(x|y)}P(y|x) }} \\ &\ge\sum_{x\in\mathcal{X}}{ P(y|x)\log{ \frac{P(y|x)P(x)}{P(x|y)} } } \\ &=\mathbb{E}_{x\sim{P(\text{x}|y)}}\big[ \log{P(y|x)} \big]-\text{KL}\big(P(\text{x}|y)\|P(\text{x})\big) \end{aligned}\]

여기서 우리가 구하고자 하는 파라미터 $\theta_{x\rightarrow{y}}$ 는 아래의 수식을 최대화 한다고 할 때, 위의 수식을 넣어 볼 수 있을 것입니다.

\[\begin{gathered} \begin{aligned} \mathcal{L}(\theta_{x\rightarrow{y}}) &=-\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\sum_{s=1}^S{ \log{P(y_s)} } \\ &\le-\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\sum_{s=1}^S{\Big( \mathbb{E}_{x\sim{P(\text{x}|y_s)}}\big[ \log{P(y_s|x;\theta_{x\rightarrow{y}})} \big]-\text{KL}\big(P(\text{x}|y_s)\|P(\text{x})\big) \Big)} \\ &\approx-\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\sum_{s=1}^S{\Big( \frac{1}{K}\sum_{k=1}^K{ \log{P(y_s|x_k;\theta_{x\rightarrow{y}})} }-\text{KL}\big(P(\text{x}|y_s)\|P(\text{x})\big) \Big)} \\ &=\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}}), \end{aligned} \\ \text{where }x_k\sim{P(\text{x}|y_s;\theta_{y\rightarrow{x}})}. \end{gathered}\]

위처럼 새롭게 정의된 $\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}})$ 을 미분하여 보면 KL-Divergence term은 없어질 것이고, 아래와 같이 파라미터는 업데이트 될 것입니다.

\[\begin{gathered} \theta_{x\rightarrow{y}}\leftarrow\theta_{x\rightarrow{y}}-\eta\nabla_{\theta_{x\rightarrow{y}}}\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}}), \\ \text{where } \nabla_{\theta_{x\rightarrow{y}}}\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}})=-\nabla_{\theta_{x\rightarrow{y}}}\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\nabla_{\theta_{x\rightarrow{y}}}\frac{1}{K}\sum_{s=1}^S{ \sum_{k=1}^K{ \log{P(y_s|x_k;\theta_{x\rightarrow{y}})} } }. \end{gathered}\]

이 수식을 해석해보면 흥미롭습니다. 두 번째 term은 반대쪽 모델 $\theta_{y\rightarrow{x}}$ 에서 $K$ 번 sampling한 $x_k$ 를 신경망의 입력으로 주었을 때, $y_s$ 에 대한 negative log likelihood를 최소화하도록 gradient를 계산하는 것을 볼 수 있습니다. 실제로 BT에서는 $K=1$ 일 때, sampling한 결과를 pseudo sentence로 삼아 신경망의 입력으로 넣어주고 있습니다. 그러므로 우리가 Back-Translation을 수행하는 것은 앞서 정의한 $\mathcal{L}(\theta_{x\rightarrow{y}})$ 를 최소화 하는 것과 같다라는 것을 알 수 있습니다.

Tagged Back-Translation을 수식으로 풀어보기

저는 사실 앞선 수식을 본 이후로 KL-Divergence term이 그렇게 사라지는 것이 영 아쉬웠습니다. 예를 들어, VAE에서는 KL-Divergencce term이 regularization term으로 매우 큰 역할을 수행하기도 하거니와, 어쨌든 KLD term이 최소화 된다면 $\log{P(y)}$ 가 좀 더 잘 최대화 될 것으로 보이기 때문입니다. 그러던차에 Noise added BT와 Tagged BT를 보고 위의 수식을 해당 방법들에 맞게 다시 전개 해보았습니다. 랜덤 변수 $c$ 를 도입해서 BT 여부를 알려주는 tag를 조건부 확률분포 함수 $\log{P(y|x,c)}$ 로 바꾸었습니다.

\[\begin{aligned} \log{P(y)} &=\log{\sum_{c\in\mathcal{C}}{ \sum_{x\in\mathcal{X}}{ P(x,y,c) } }} \\ &=\log{\sum_{c\in\mathcal{C}}{ \sum_{x\in\mathcal{X}}{ P(y|x,c)P(x|c)P(c) } }} \\ &=\log{\sum_{c\in\mathcal{C}}{ \sum_{x\in\mathcal{X}}{ \frac{P(y|x,c)P(x|c)}{P(x|y,c)}P(x|y,c)P(c) } }} \\ &\ge\sum_{c\in\mathcal{C}}{P(c) \sum_{x\in\mathcal{X}}{P(x|y,c) \log\frac{P(y|x,c)P(x|c)}{P(x|y,c)} } } \\ &=\mathbb{E}_{c\sim{P(\text{c})}}\bigg[ \mathbb{E}_{x\sim{P(\text{x}|y,c)}}\Big[ \log{P(y|x,c)} \Big] -\text{KL}\Big(P(\text{x}|y,c)\|P(\text{x}|c)\Big) \bigg] \end{aligned}\]

위의 수식에 따르면, 샘플링된 $c$ 에 따라 $x$ 를 실제 parallel corpus에서 활용하거나 파라미터 $\theta_{y\rightarrow{x}}$ 의 신경망에서 샘플링하여 타깃 파라미터 $\theta_{x\rightarrow{y}}$ 의 신경망에 tag $c$ 와 함께 넣어, log-likelihood인 $f(x,c;\theta_{x\rightarrow{y}})$ 를 구할 것 입니다. 즉, 여기서 $P(\text{x}|y,c=\text{BT})$ 는 이미 반대쪽 모델에 noise가 추가된 형태라고 보아야 할 것입니다.

이때 KLD term을 해석해본다면 재미있을 것 같습니다. 좌변을 최대화 하기 위해서는 KLD term이 최소화 되어야 할 것입니다. 따라서 분포 $P(\text{x}|y,c)$ 와 $P(\text{x}|c)$ 는 최대한 같아져야 할 것입니다. – 여기서 $c\ne\text{BT}$ 인 경우는 일단 제외하고 생각하도록 하겠습니다. 이에따라 랜덤변수 $\text{x}$ 와 $\text{y}$ 의 mutual information이 최소가 될 것입니다. 즉, 이것의 의미는 $y$ 의 정보에 상관 없이 pseudo corpus 자체의 언어모델 $P(\text{x}|c)$ 를 따르도록 될 것이란 것이고, 또한 이로 인해 $y\rightarrow{x}$ 의 번역 품질이 낮아질 것이라고 예상할 수 있습니다. 실제로 Noise added BT[7]의 경우에 일부러 noise를 섞어 번역의 품질을 희생시켰으며, 그 과정에서 bias를 학습하지 않도록 할 수 있었습니다.

사족: 샘플링 방식을 학습하는 것은 어떨까?

앞서 언급한대로 $x\sim{P(\text{x}|y,c)}$ 과정에서 이미 우리는 noise가 추가된 형태로 이해해볼 수 있을 것 같습니다. 즉, 기존의 $\theta_{y\rightarrow{x}}$ 함수를 한번 더 감싸서 noise added BT를 구현할 수도 있을 것입니다. 또한 KL term에서 $P(\text{x}|y,c)$ 는 $P(\text{x})$ 가 아닌 $P(\text{x}|c)$ 와 가까워지도록 하였기 때문에, 만약 우리가 noise를 섞어주는 방식도 parameterize(e.g. neural network)한다면 학습에 활용할 수 있을 것입니다.

정리하며

이번 포스팅에서는 monolingual corpus를 통해 NMT의 성능을 향상시키는 가장 대표적인 방법인 Back-Translation에 대해서 살펴보았습니다. BT는 간단한 방법과 이에 비해 높은 성능 향상을 인해 널리 사랑받고 있는 방법 중 하나입니다. 하지만 아쉽게도 low-resource NMT 상황이 아니면, original text보단 translationese를 번역하는데 대부분의 성능 향상이 집중되는 것을 확인할 수 있었습니다. 그렇다고 해서 BT가 별로다라는 이야기는 아닙니다. 어쨌든 low-resource NMT에서는 매우 강력한 힘을 발휘하고 있으며, high-resource(?) NMT에서도 어쨌든 득실을 따져보면 득이 더 크기 때문입니다.

또한 기존의 BT는 직관에 의해서 보통 설명이 되기 마련이었는데, [9]와 같은 방법을 통해 우리는 BT를 좀 더 수식적으로도 이해할 수 있었고, 한 발 더 나아가 Tagged BT에 대해서도 새롭게 수식으로 접근해보는 시간도 가져보았습니다. 위와 같이 수식을 통해 접근을 함으로써, 우리는 BT에 대한 더 나은 이해와 더 높은 성능 개선을 위한 한 걸음을 더 나아갈 수 있을 것이라고 생각합니다.

참고문헌

Introduction to Deep Time-series Anomaly Detection

이번 포스팅에서는 시계열(time-series) 또는 시퀀셜(sequntial) 데이터에 대한 anomaly detection 기법을 이야기하고자 합니다. 사실 시계열 데이터는 데이터의 발생 시점(e.g. interval)도 중요한 feature인데 반해, 단순한 시퀀셜 데이터는 보통 순서 정보만 활용됩니다. 하지만 딥러닝의 대부분의 모델들은 기본적으로 시퀀셜 데이터만 다루도록 설계되어 있습니다. 이 포스팅은 딥러닝을 활용한 일반적인 방법론에 대해 이야기하고자 하므로, 시계열 데이터의 샘플간 time interval이 동일하다고 가정하고 seasonality와 같은 issue는 배제하고 이야기하고자 합니다. 즉, 비록 시계열 데이터이긴 하지만 일반적인 시퀀셜 데이터와 같이 다루도록 하겠습니다. 추후 다른 포스팅에서 interval 또는 seasonality와 같은 issue에 대해서 다루도록 하겠습니다. – 딥러닝을 활용한 이상탐지에 대한 앞선 포스팅[1, 2, 3]도 참고 바랍니다.

Previous Methods

사실 이상탐지의 대부분 application들은 의외로 시계열 데이터인 경우가 많습니다. Computer vision 분야에서의 image anomaly detection과 같은 case를 제외한다면, 특히 numeric data 또는 tabular data인 경우 대부분이 시계열 데이터로 구성되어 있는 경우가 많습니다. 따라서 예전부터 이상탐지 분야에서 시계열 데이터에 대한 이상탐지에 대한 연구가 많이 이루어져 왔습니다. 하지만 이에 반해, 현재 딥러닝에서의 이상탐지 연구들은 대부분 iid 기반이 많은 것이 사실입니다.

Univariate Time-series Anomaly Detection

심장박동

보통 시계열 이상탐지 연구는 univariate time-series 데이터에 대해서 연구되어왔습니다. Image에서의 이상탐지라고 한다면, 주어진 이미지가 정상 범위에서 벗어날 경우 이것에 대해서 탐지하는 문제가 될 것입니다. 이에 반해 시계열 이상탐지 문제는 주어진 기간동안의 신호들이 정상 범위에서 벗어날 경우 이것에 대해서 탐지할 수 있어야 합니다. 예를 들어 심장 박동의 이상을 탐지하는 문제라고 한다면, 주어진 시간동안의 심장의 움직임에 대한 신호들을 가지고 해당 시간 내에 비정상적인 심장의 움직임이 있었는지 탐지하는 문제가 될 것입니다.

딥러닝 이전에는 DTW(Dynamic Time Warping)이나 ARIMA를 활용한 방법들도 많이 연구되었습니다. 딥러닝 모델을 활용해서도 여러가지 연구가 진행되었으나, 오늘의 주요 주제는 아니므로 넘어가도록 하겠습니다.

Multivariate Time-series Anomaly Detection

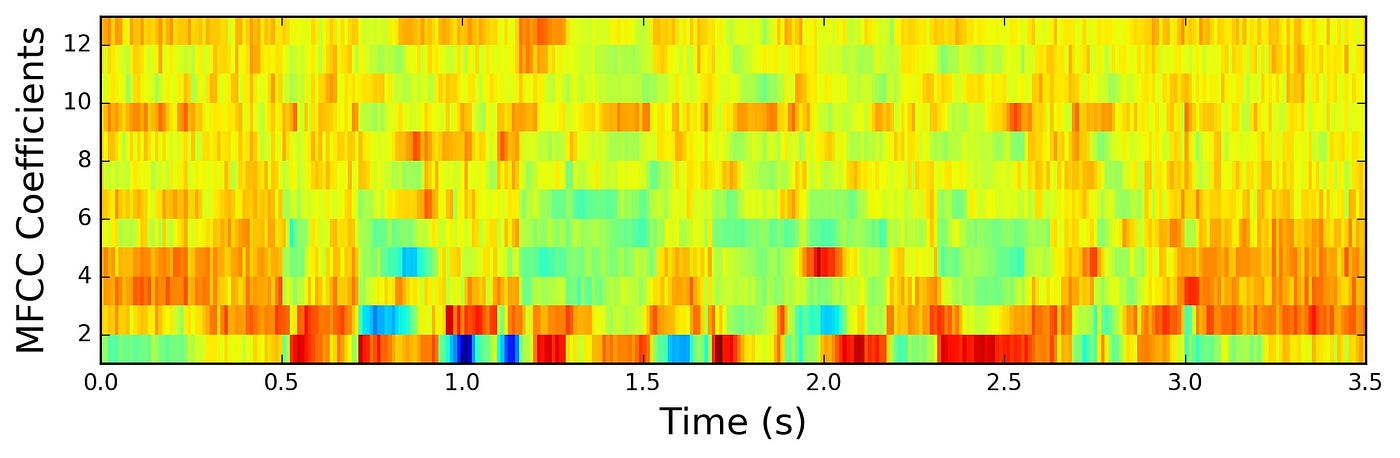
MFCC 출처: https://medium.com/prathena/the-dummys-guide-to-mfcc-aceab2450fd

사실 오늘 주로 다루고자 하는 주제는 multivariate time-series 데이터에 대한 이상탐지입니다. 예를 들어, 위의 그림은 univariate time-series 데이터인 오디오 신호를 MFCC로 나타낸 것입니다. 위의 그림에서 x축은 시간을 나타내고, y축은 주파수 대역을 의미합니다. 따라서 특정 시간에 발생한 전체 주파수 대역에서의 신호의 세기가 multivariate vector로 나타내어질 수 있을 것입니다. 그럼 정해진 시간동안의 multivariate vector들의 시퀀스가 주어졌을 때, 해당 벡터들의 시퀀스가 정상 범위 내에 있는지 판단하는 문제가 될 것입니다.

사실 univariate time-series anomaly detection은 심장박동 이상탐지와 같은 문제에서는 훌륭하게 동작할 수 있지만, 많은 문제에 그대로 적용되기에는 어려움이 있습니다. 위의 오디오 신호에 대한 예제를 포함하여, 많은 반례를 생각해볼 수 있습니다. 예를 들어 제가 DEVIEW 2019에서 발표[4]할 때 데모로 소개해드렸던 로봇팔 이상탐지의 경우도 해당 될 수 있습니다.

해당 로봇팔은 6개의 축을 가지고 있습니다. 즉, 6개의 전기모터로 구성되어 있고, 이 모터에 들어가는 전류값(current)을 신호로 삼아서 이상탐지 문제를 접근해 볼 수 있을 것입니다. 이때, 각 축 별로 univariate time-series 이상탐지 모델을 만들어 적용해볼 수도 있을 것입니다. 하지만 이 경우에는 각 축간의 상호작용은 전혀 파악할 수 없을 것입니다. 예를 들어 1번 축이 높은 값일 때는 다른 축들이 낮은 값을 지녀야 한다던지와 같은 상황에 대해서는 대처할 수 없을 것입니다. 따라서 이러한 문제에서는 multivariate time-series 모델을 도입하여, 각 feature 사이의 상관관계까지도 학습할 수 있습니다.

6축 로봇팔 예제

이때, 기존의 shallow 기법들은 univariate 위에서의 time-series를 다루기에도 벅찬 상황이기 때문에, 딥러닝을 활용한 이상탐지 모델링 기법이 큰 힘을 발휘할 수 있습니다.

Deep Time-series Anomaly Detection

재미있게도 일찍이 딥러닝 이전의 시절에도 LSTM의 존재는 있었지만, 당시에는 데이터와 컴퓨팅 파워의 부족으로 인해서 부담스러운 존재였던 것도 사실입니다. 하지만 이제는 이전의 문제들이 대부분 해결되어 LSTM 따위는 아무런 부담없이 학습할 수 있게 되었습니다. 따라서 우리가 풀고자 하는 데이터가 시퀀셜 또는 시계열의 성격(샘플이 매번 독립적으로 같은 분포에서 샘플링 되는 것이 아니라면)을 갖고 있다면, RNN 계열의 모델을 활용해 보는 것도 매우 좋은 방법일 것 입니다.

Using IID Models with Flatten Vectors

하지만 바로 RNN과 같은 시퀀셜 모델을 도입하기에 앞서, time-series 데이터를 1차원의 tensor로 flatten하여 일반적인 iid 모델에 넣어보는 것도 좋은 시도(or baseline)가 될 수 있습니다.

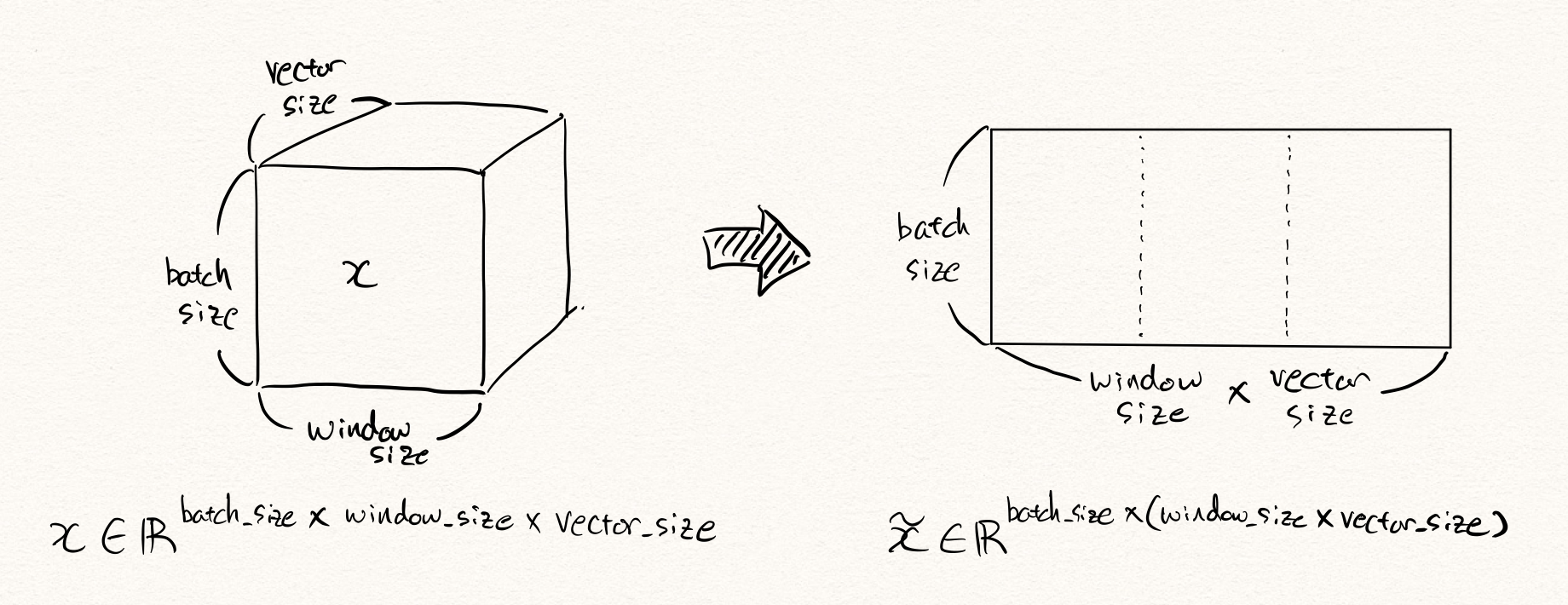
flatten 예제

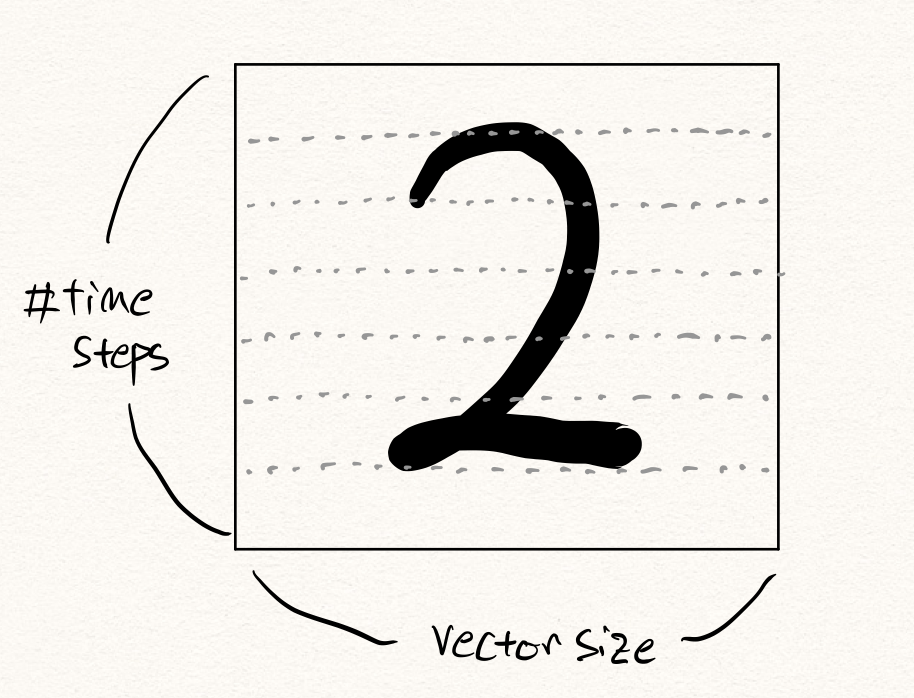
6차원 time-series 로봇팔 데이터를 예로 들어 보겠습니다. 만약 해당 데이터가 10Hz의 샘플링 주기를 가지고 있고, 우리는 약 5초간의 동작 데이터를 활용하여 이상을 탐지하고자 한다면, 한번의 이상탐지를 위해 주어진 데이터는 아래와 같은 형태를 따를 것입니다.

\[x\in\mathbb{R}^{10\times5\times6}\text{, where }x\sim{P_D(\text{x})}.\]

이때, 이것을 flatten한다면 $6\times10\times5=300$ 차원의 벡터 $\tilde{x}$ 가 될 것입니다. 그럼 이 300차원의 벡터를 오토인코더(autoencoder) $\mathcal{A}$ 에 넣어 학습 및 추론을 수행할 수 있을 것입니다. 이때 우리는 예전 포스팅에서 다루었던 대로 복원 오차(reconstruction error) 또는 RaPP[5]와 같은 방법들을 통해 이상 샘플을 탐지할 수 있습니다.

\[\begin{gathered} \text{AnomalyScore}(x)=||\tilde{x}-\mathcal{A}(\tilde{x})|| \\ \text{or} \\ \text{RaPP}(x)=\sum_{i=0}^{\ell}{||g_{:i}(\tilde{x})-g_{:i}\circ\mathcal{A}(\tilde{x})||}\text{, where }\mathcal{A}=f_{:\ell}\circ{g_{:\ell}}. \end{gathered}\]

하지만 이러한 경우(특히 fully-connected layer와 같은 레이어들로 구성되어 있는)에는, 시계열의 특성을 활용한다기보단 모든 feature들과의 상관관계를 모두 따져보는 것이기 떄문에, 필요 이상으로 배워야 하는 정보들이 많아지고 이에 따라 모델 웨이트 파라미터들도 훨씬 많아져서 모델이 학습하는데 불리하게 작용할 수 밖에 없습니다.

Single RNN based Methods

그럼 이제 본격적으로 RNN 계열 모델들을 활용하는 방법을 이야기 해보겠습니다. 가장 간단한 방법으로는 하나의 RNN을 활용한 generative modeling을 생각해볼 수 있습니다. 이를 위해서는 아래와 같이 RNN $f$ 가 $x_{<t}$ 를 입력 받아, $x_t$ 를 예측하는 형태가 될 것입니다.

\[\hat{\theta}=\text{argmax}\sum_{t=1}^{T}{\log{P(x_t|x_{<t};\theta)}}\text{, where }x_{1:T}=\{x_1,\cdots,x_T\}.\]

그럼 이때 likelihood는 아래와 같이 계산될 수 있습니다.

\[\log{P(x_t|x_{<t};\theta)}=\|x_t-f_\theta(x_{<t})\|\]

이때 그럼 우리는 이 likelihood를 anomaly score로 삼아 이상탐지를 수행할 수 있을 것입니다. – 기존 오토인코더 방식에서는 reconstruction error가 likelihood가 됩니다.

\[\text{AnomalyScore}(x_{1:T})=\sum_{t=1}^T{\|x_t-f_\theta(x_{<t})\|}\]

즉, RNN은 다음 time-step의 값을 예측하는 task를 통해 자연스럽게 정상 분포를 학습하게 되고, 비정상 샘플이 주어진다면 likelihood의 값이 낮게 나오게 될 것이므로 우리는 이를 활용하여 시계열 이상탐지를 수행할 수 있는 것입니다.

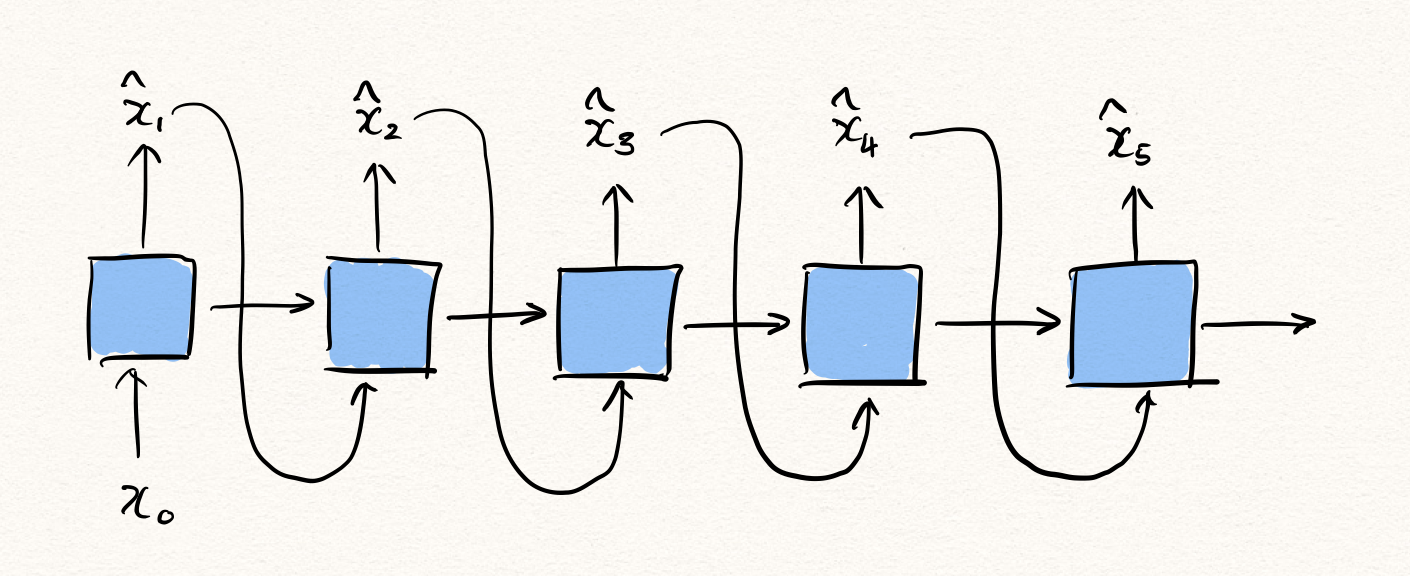
Single RNN의 generation 예제

하지만 아쉽게도 이 모델은 auto-regressive(자기회귀) 특성을 가지므로 한계가 있습니다. 한 방향으로만 추론이 이루어지기 때문에, $x_t$ 에 대해서 추론을 수행하고자 할 때, $t$ 이전 시점의 데이터들로부터만 정보를 얻어올 수 있습니다. 하지만 $t$ 이후 시점으로부터도 정보를 얻어와 $x_t$ 를 추론할 수 있다면 훨씬 더 정확한 예측을 수행할 수 있을 것입니다.

이것은 이상탐지 문제는 generation에 집중하는 task가 아니기 때문이라고 해석해 볼 수 있습니다. 예를 들어 기계 번역(machine translation)과 같은 언어 모델링(language modeling) task에서는 신경망이 입력과 다른 새로운 문장을 출력해 내야 하는 것이지만, 이상탐지 task에서는 주어진 샘플을 얼마나 잘 똑같이 복원해 내는지가 관건이기 때문이라고 볼 수 있습니다. 즉, 다시말하면 기존의 NLG task에서는 입력과 출력이 다른 형태이지만, 이상탐지 task에서는 입출력이 같은 형태이기 때문에 다른 접근법이 가능하다는 것입니다.

Encoder-Decoder based Methods

그럼 한 발 더 나아가 sequence to sequence와 같은 encoder + decoder 기반의 아키텍처를 생각해볼 수 있습니다.

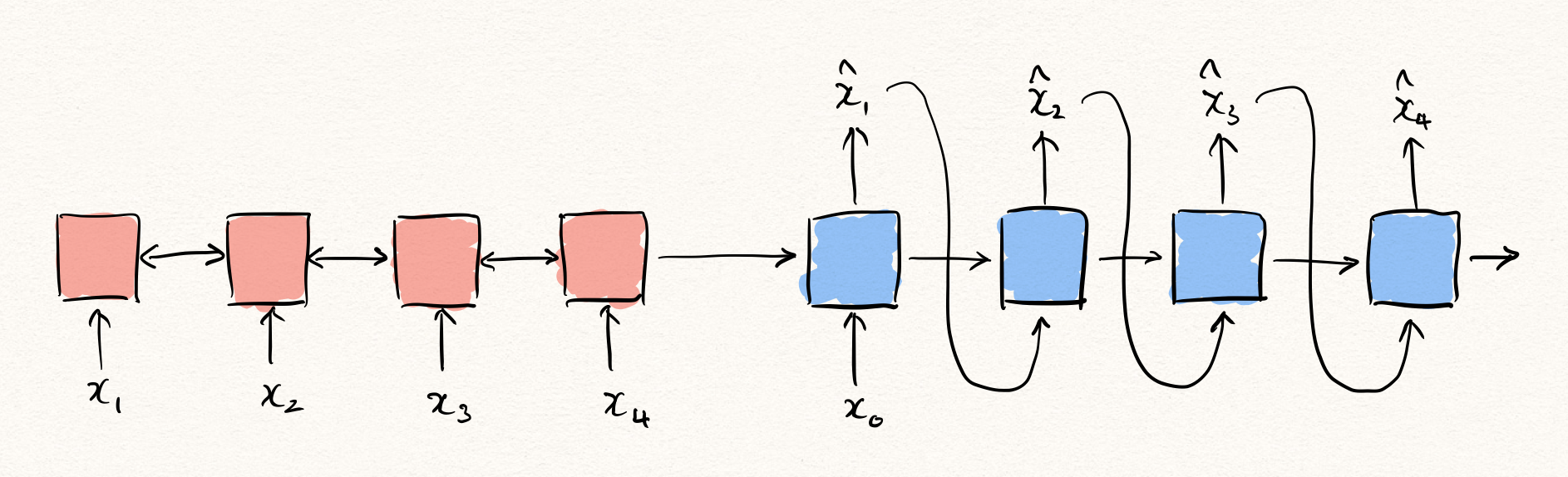
Sequence Autoencoder 예제

다만, 이 아키텍처는 주어진 입력을 그대로 복원해내야 하기 때문에, 기존의 sequence to sequence와 차별하기 위해서 sequence autoencoder(SeqAE)라고 부르도록 하겠습니다. 이 SeqAE는 여전히 auto-regressive한 decoder를 갖고 있지만, 어쨌든 encoder에서 주어진 모든 time-step을 볼 수 있었기 때문에, 앞서 설명한 아키텍처보다는 조금 더 유리한 부분을 가질 수 있습니다.

\[\hat{\theta}=\text{argmax}\sum_{t=1}^T{\log{P(x_t|x_{<t},z;\phi)}}\text{, where }z=g(x_{1:T};\psi)\text{ and }\theta=\{\phi,\psi\}.\]

이때 encoder $g$ 로부터 얻은 latent representation $z$ 는 오토인코더 관점에서 보면 bottleneck에서의 variable이라고 생각해 볼 수 있습니다. 즉, 우리는 encoder를 통해 $x_{1:T}$ 를 압축하여, decoder를 통해 순차적으로 풀어내는 것이라 볼 수 있습니다.

Attention?

이때 흔히 성능을 개선하기 위한 포인트로 attention을 추가하는 것을 고려해볼 수 있습니다. 예를 들어 기계번역을 위한 sequence to sequence(seq2seq) 아키텍처에서 attention이 추가 되면, seq2seq 내부 RNN의 hidden state의 capacity 부족 등의 문제로 인한 성능 하락을 막을 수 있습니다. 따라서 attention은 자연어처리 분야에서 매우 중대한 발전이라고 볼 수 있습니다.

하지만 이상탐지 문제 해결 관점에서는 attention을 곧바로 적용하기에는 무리가 있습니다. 기계번역과 같은 task에서는 더 나은 문장을 생성하기 위해서 RNN의 hidden state를 극복하기 위한 대안으로 제시되었지만, 이상탐지에서는 bottleneck의 latent representation $z$ (hidden state)에 압축된 정보가 무엇인지가 중요합니다. 비정상 샘플이었다면 정상적으로 압축이 수행되지 않아, $z$ 에 복원을 위한 충분한 정보가 담겨있지 않을 것이기 때문입니다. 하지만 여기서 우리가 attention을 사용한다면, $z$ 의 압축 품질 여부와 상관 없이 decoder는 attention을 통해 encoder에서 충분한 정보를 access할 수 있을 것이기 때문입니다. 따라서 attention을 시도해 보는 것은 좋지만, 이 문제를 해결하는 방향이 함께 시도[6]되어야 할 것이라 생각합니다.

Teacher Forcing

사실 앞서 RNN을 통해 이상탐지를 수행하는 방법에 대해서 설명할 때, 빼 놓은 부분이 있습니다. 바로 학습 및 추론 방법 입니다. 먼저, 추론 상황을 가정해보겠습니다. 자연어생성(NLG)과 같은 Auto-regressive한 task를 수행하는 경우, 보통은 decoder를 통해 출력을 뱉어낼 때 decoder의 입력은 이전 time-step의 decoder의 출력이 됩니다.

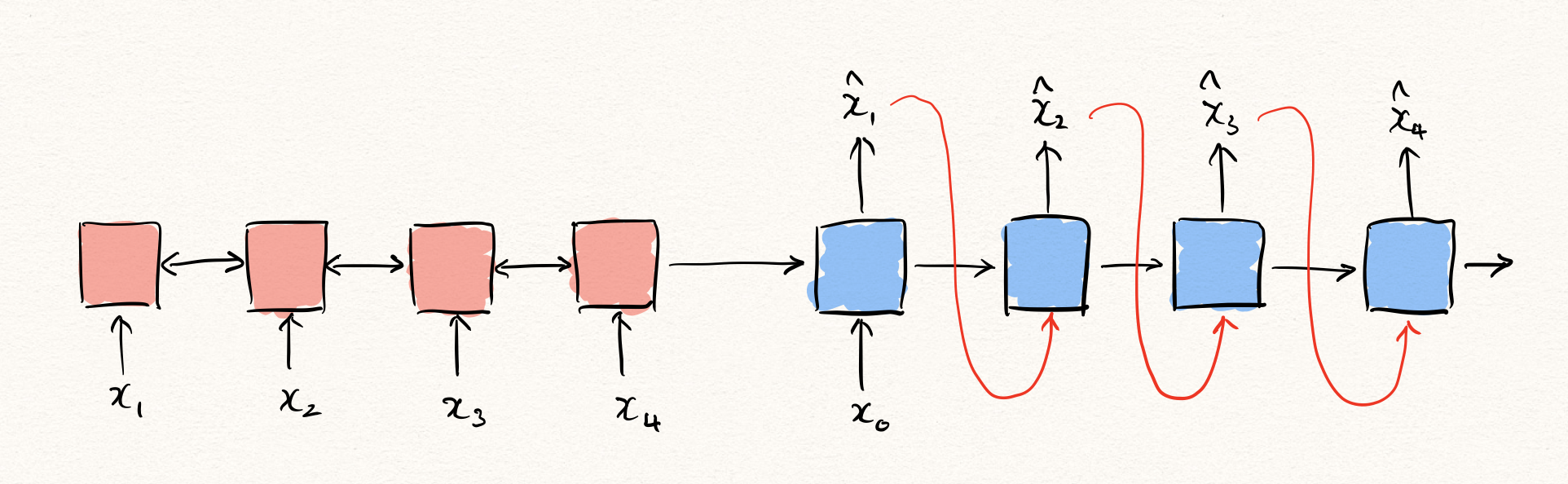
Sequence Autoencoder의 generation 예제

\[\hat{x}_t=\text{argmax}\log{P(\text{x}_t|\hat{x}_{<t};\theta)}\]

하지만 문제는 학습을 수행할 때는 이와 같은 방법으로 진행하는 것은 문제가 될 수 있습니다. 우리는 likelihood를 maximize 하기 때문에, 원래의 정답 $x_t$ 와 decoder $f$ 의 출력 $\hat{x}_t$ 의 차이를 구합니다. 이것은 수식으로 나타내면 아래와 같습니다.

\[\begin{aligned} \mathcal{L}(\theta)&=-\sum_{t=1}^T{\log{P(x_t|x_{<t};\theta)}} \\ &=-\|x_1-f_\theta(x_0)\|_2^2-\|x_2-f_\theta(x_{0:1})\|_2^2-\cdots-\|x_T-f_\theta(x_{0:T-1})\|_2^2 \end{aligned}\]

즉, decoder의 입력으로 $\hat{x}{<t}$ 가 아닌, $x{<t}$ 가 주어졌기 때문에, 가능한 것입니다. 만약 학습할 때에 $\hat{x}_{<t}$ 가 주어진 상태에서 decoder의 출력값과 $x_t$ 와의 MSE를 구한다면, 우리는 Maximum Likelihood Estimation (MLE)를 한다고 할 수 없는 것입니다. 따라서 딥러닝에서 MLE를 통해 시퀀셜 데이터를 학습할 때에는 teacher forcing이라는 방법을 통해 학습을 수행하는 것이 보통입니다.

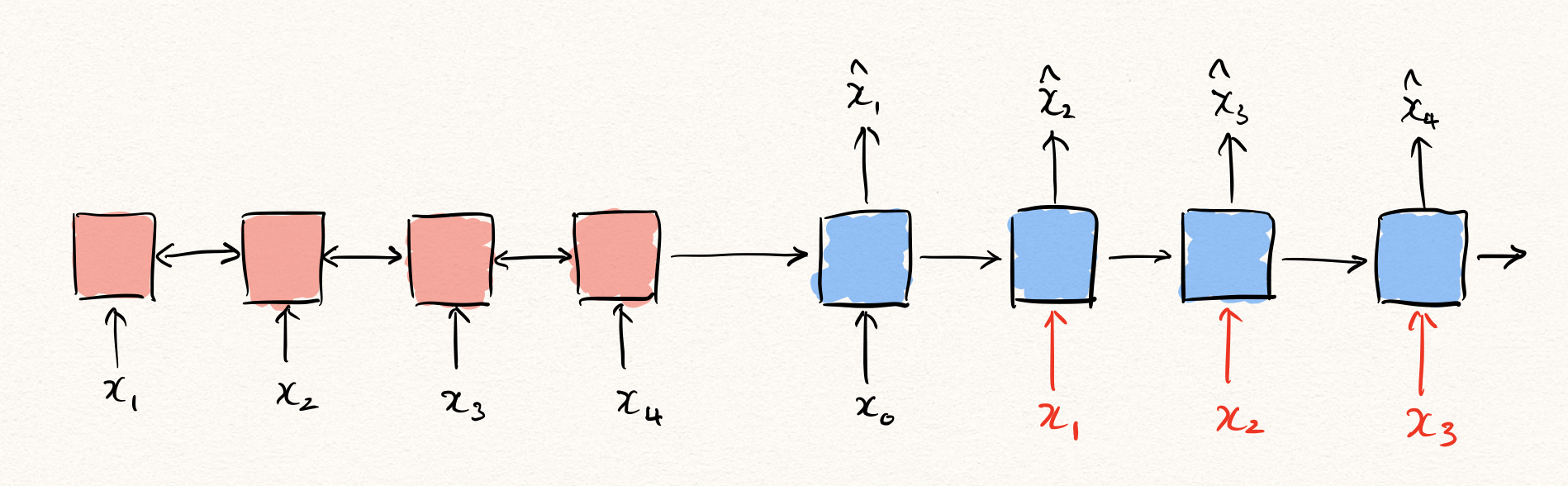
Sequence Autoencoder에서의 Teacher Forcing 예제

Teacher forcing은 위 그림과 같이 학습 과정에서 decoder의 이전 time-step의 출력이 아닌 이전 time-step의 실제 정답을 decoder에 입력으로 넣어주는 것입니다. 우리는 이런 teacher forcing을 통해 auto-regressive task에서 RNN을 MLE를 통해 학습할 수 있게 됩니다.

문제는 여기에서 발생하게 됩니다.

How to Inference: Likelihood vs Generation

문제를 디테일하게 이야기하기에 앞서, SeqAE에서의 이상탐지를 위한 추론 방법에 대해서 좀 더 이야기하려 합니다. 앞서는 단순히 NLG task와 같은 추론 방법인 generation에 대해서 이야기 했는데, 사실 iid 데이터의 오토인코더를 활용한 reconstruction error 기반의 이상탐지 방법은 분포가 gaussian이라는 가정 하에 likelihood를 구하는 것이라고 볼 수 있습니다.

따라서, SeqAE에서도 generation이 아닌, likelihood를 통해 reconstruction error를 구하고, 그것을 통해 이상탐지 추론을 수행해야 하는 것은 아닌가 하는 합리적인 의심이 생길 수 있습니다. 그럼 위에서 적은데로 teacher forcing 방법을 추론에서 수행할 수도 있다는 이야기겠죠. 특히, NLG와 달리 이상탐지 task에서는 입력을 그대로 복원해내기 때문에, SeqAE가 출력해야 하는 값을 알고 있다는 점에서 teacher forcing이 가능합니다. – 이와 반대로 기계번역과 같은 NLG task에서는 test과정에서는 seq2seq의 출력값을 모르기 때문에 generation을 수행할 수 밖에 없습니다.

그런데 문제는 teacher forcing을 통해 reconstruction을 구하게 된다면 너무나도 쉬운 task가 되어버린다는 것입니다. 예를 들어 아래와 같이 MNIST를 시퀀셜 데이터로 취급해서 이상탐지를 똑같이 수행해볼 수 있을겁니다. 즉, $28\times28$ 의 MNIST 이미지를 28차원의 벡터가 28 time-step 존재하는 시퀀셜 데이터로 생각해볼 수 있을 것입니다.

MNIST 숫자 2를 sequential 데이터로 취급할 때

그럼 teacher forcing을 추론에서 수행하게 된다면, decoder는 이전 time-step에서 틀린 출력 $\hat{x}{t-1}$ 을 뱉어냈더라도, 현재 time-step의 입력으로 정답 $x{t-1}$ 을 받게 될겁니다. 그럼 현재 time-step의 출력 $\hat{x}t$ 를 예측하는 것은 너무나도 쉬워지게 됩니다. 당장 MNIST의 경우에만 보더라도 $x{t-1}$ 과 거의 유사한 픽셀값을 뱉어내면 거의 맞출테니까요. 즉, 학습 때 보지 못한 형태의 이미지가 들어오더라도 같은 방법을 통해서 대충 맞출 수 있게 되는 것입니다.

그러므로 우리는 SeqAE와 같은 모델에서는 teacher forcing을 통해 likelihood를 구하는 것이 아닌, generation 방식으로 통해 이상탐지의 추론을 수행해야 함을 확인할 수 있습니다. 즉, 원래 평소(NLG task등에서 하던 방법)에 하던대로 하면 됩니다.

Begining of Posterior Collapse

그런데 문제는 또 남아있습니다. teacher forcing을 통해 학습을 진행할 때에도 마찬가지 상황이 발생한다는 것입니다. 특히나 NLG와 같은 discrete value를 출력하는 task가 아니라 continuous value를 뱉어내는 task이기 때문에, $x_{t-1}$ 와 $x_t$ 의 차이가 적어서 생기는 문제로도 생각해볼 수 있습니다. 따라서 teacher forcing을 통해 학습을 수행할 때에도, 너무나도 쉬운 나머지 encoder로부터 많은 정보를 받을 필요가 없어지게 됩니다. 예를 들어 아래와 같이 2 또는 3에 대해서 학습할 때, 한번의 도움만 있으면 충분하지 않을까요?

MNIST 2와 3은 일부 row까지는 매우 비슷한 전개를 보일 것

그럼 encoder는 주어진 샘플에 대해서 많은 정보를 인코딩하지 않도록 학습될겁니다. 이것은 결국 추론 단계에서 비정상 샘플이 주어졌을 때, 안좋은 영향을 끼치게 될 것입니다. 이렇게 encoder가 어떤 샘플이 주어지든 비슷한 latent representation으로 인코딩하게 되는 현상을 posterior collapse라고 부릅니다. 물론 위의 예제에서처럼 어쨌든 2와 3을 구분하기 위한 정보가 어느정도는 담겨있을 것이기 때문에, 아무런 정보가 없지는 않겠지만 posterior collapse의 경향이 나타난다고 볼 수 있습니다.

Needs of Sequence Variational Autoencoder (SeqVAE)

우리는 앞선 포스팅에서 VAE가 Variational Information Bottleneck(VIB)를 가지고 있어서 이상탐지 task에서 더 뛰어난 성능을 보인다고 이야기 한 바 있습니다. 그럼 마찬가지로 SeqAE에서도 한발 더 나아가 SeqVAE를 생각해 볼 수 있을 것입니다. 문제는 이 SeqVAE가 posterior collapse에 매우 취약하다는 것입니다.

\[\mathcal{L}(\phi,\psi)=-\mathbb{E}_{z\sim{q(\text{z}|x;\psi)}}\Big[\log{p(x|z;\phi)}\Big]+\text{KL}\Big(q(z|x;\psi)\|p(z)\Big)\]

위와 같이 VAE 또는 SeqVAE는 첫 번째 reconstruction term과 함께 두 번째 KL-divergence term도 최소화해야 합니다. 문제는 SeqVAE는 앞서 언급한 문제 때문에 디코더는 아주 적은 정보만 있어도 디코딩을 잘 할 수 있습니다. 더욱이 KLD term이 있기 때문에 인코더는 더더욱 아무 일을 하지 않으려 노력하게 됩니다. – 아마 인코더는 어떤 샘플이 들어오더라도 $\mu=0$ , $\sigma=1$ 을 뱉어내고 싶을 겁니다. 즉, SeqVAE는 앞서 언급한 posterior collapse 문제를 더욱 심하게 겪게 됩니다.

그럼 이런 posterior collapse가 심하게 존재하고 있는 상황에서는 인코더에 어떤 샘플이 주어지더라도 인코더의 출력값 latent representation $z$ 는 변화가 없을(KLD term이 0이 될) 것이기 때문에, 디코더는 generation형식으로 inference를 수행하게 되면 어떤 샘플이 들어오든 항상 같은 출력값을 뱉어내게 됩니다. 마치 Generative Adversarial Networks (GAN)에서의 mode collapse와 비슷한 현상이 결과로 나타나는 것이지요. – 이러한 현상이 나타나는 원인은 다릅니다.

따라서 이러한 VAE의 posterior collapse를 해결하기 위한 연구들[7, 8, 9, 10, 11]도 많이 이루어져 왔습니다. 하지만 대부분은 text domain에서의 문제 셋팅(discrete value + variable length)에 집중하고 있고, continuous data에 대한 이상탐지 문제에서의 posterior collapse 현상에 대한 해결책을 제시하는 연구는 아직 많지 않은 것이 사실입니다. 다행히도 기존의 연구들이 집중하고 있는 문제 셋팅이 이상탐지에 비해서 좀 더 어려운 문제 셋팅이다보니, 기존의 연구들로부터 많은 도움은 받을 수 있겠지만 본격적인 연구가 이루어지지 않았다는 것이죠. 따라서 sequential modeling을 활용한 이상탐지 문제 해결을 위한 연구들이 본격적으로 많이 이루어져야 함을 알 수 있습니다.

Conclusion

이번 포스팅에서는 딥러닝 모델을 활용한 시계열(또는 시퀀셜) 데이터에 대한 이상탐지 방법과 어떤 어려움들이 있는지 살펴보았습니다. 사실 단순히 RNN이나 seq2seq와 같은 아키텍처를 쓰면 모든 문제가 해결될 것 같지만, 이 포스팅에서 살펴본 것처럼 고려해야 할 점들이 많이 남아 있고, 아직 풀어야 할 문제들도 남아있는 것이 사실입니다. 다음 포스팅에서는 앞서 언급한 문제들을 마키나락스에서 해결한 사례를 공유하고자 합니다.

References

RaPP - Novelty Detection with Reconstruction along Projection Pathway

이번 포스팅은 마키나락스에서 2020년 4월에 에티오피아에서 열리는 ICLR에 출판한 페이퍼인 RaPP [1] 방법에 대해서 다루도록 하겠습니다. 이 방법은 기존의 오토인코더(autoencoders, AE)에서의 reconstruction error 기반의 이상탐지(anomaly detection)를 확장한 것으로, 학습을 위한 training objective는 수정하지 않고 테스트 과정에서의 anomaly score metric만을 수정하여 이상탐지 성능을 끌어올린 것에 의의가 있습니다. 이 포스팅을 통해서 RaPP의 motivation과 직관적인 해석, 그리고 수식적인 해석과 실험 결과를 전달하고자 합니다. 추가로 페이퍼에 미처 적지 못했던 RaPP의 인사이트를 공유하고자 합니다.

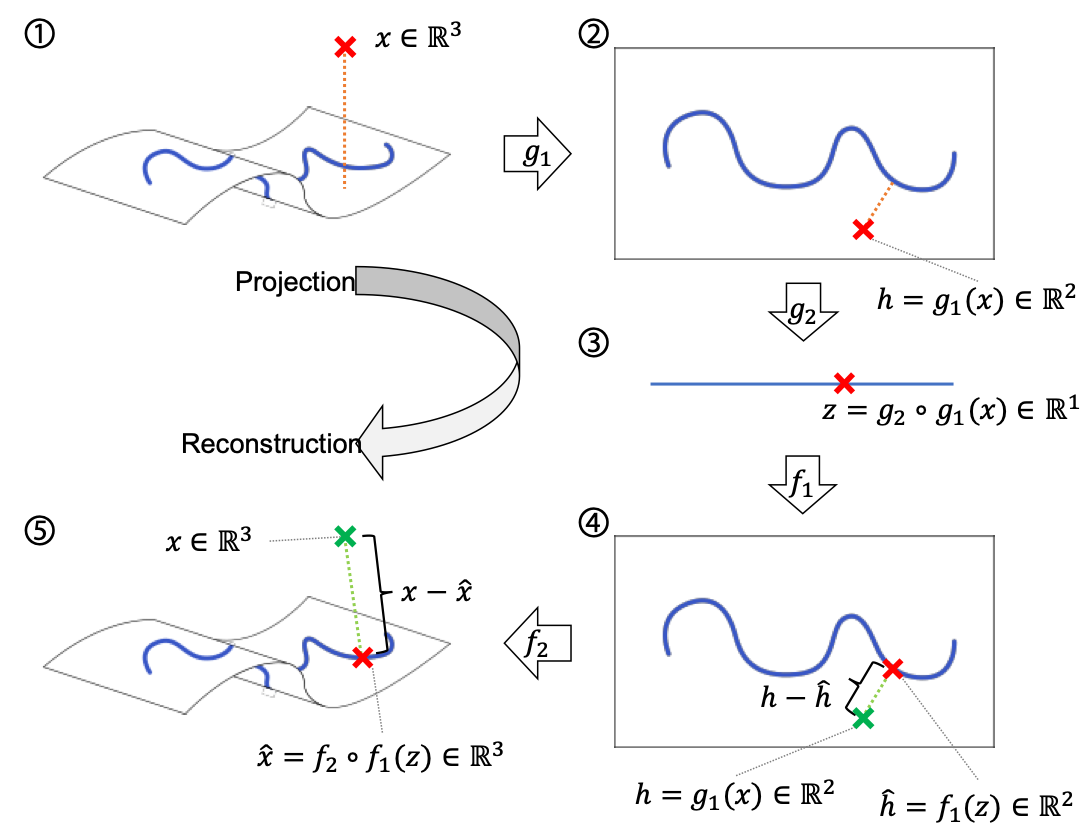
Overall Process

좀 더 나아가기에 앞서, RaPP의 동작 방식에 대해서 설명하고자 합니다. 앞서 언급하였듯이 RaPP는 기존의 다양한 오토인코더 위에서 동작하는 anomaly score metric 입니다. 따라서 오토인코더의 training objective의 수정 없이, 단순히 이미 학습된 오토인코더를 활용하여 더 나은 이상탐지 성능을 제공합니다.

RaPP의 동작 원리는 다음과 같습니다.

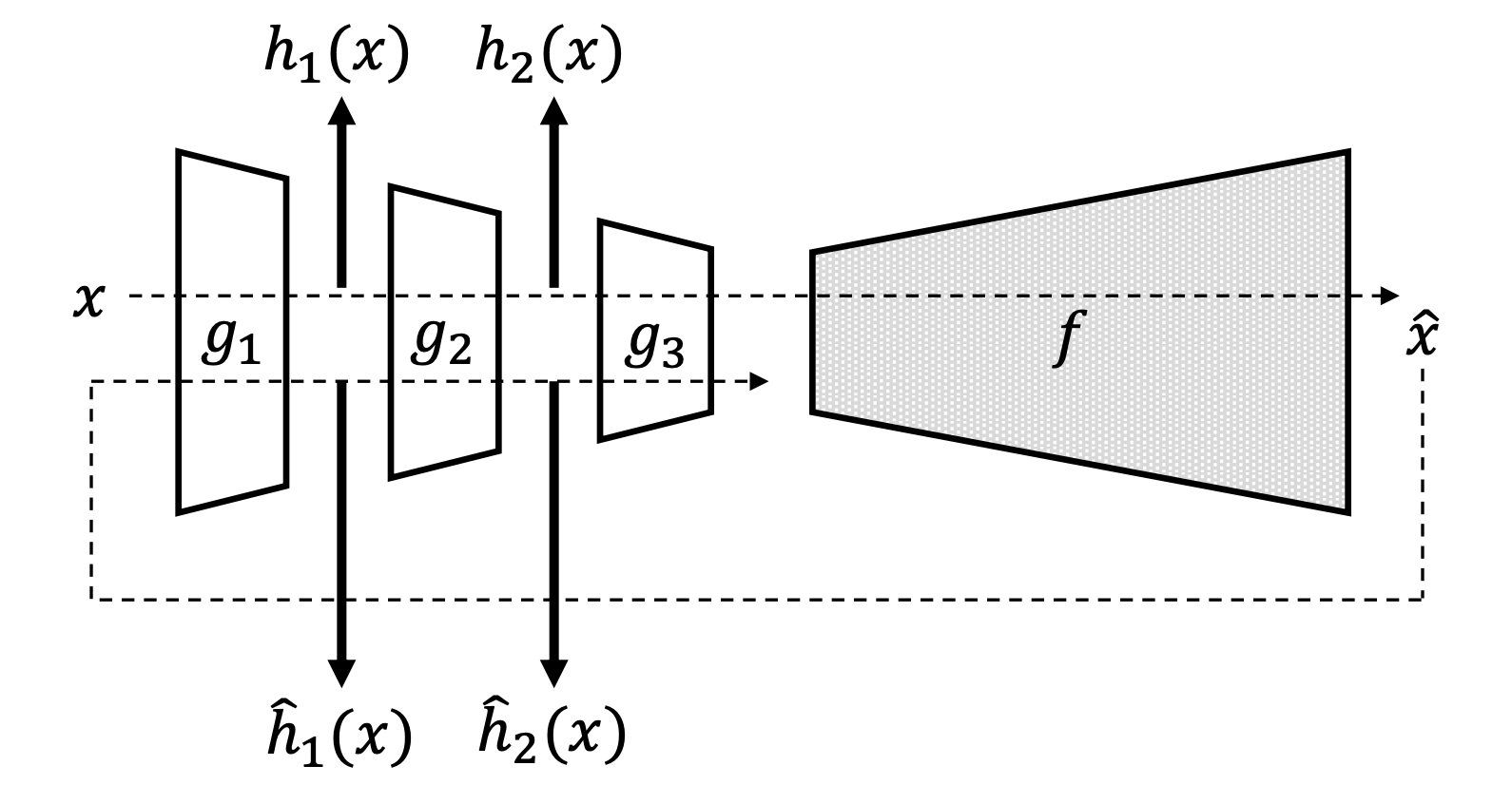
RaPP 수행 방법

먼저, 입력 샘플 $x$ 를 오토인코더 $A$ 의 인코더 $g$ 와 디코더 $f$ 에 차례로 통과시킵니다. 그럼 우리는 결과물 $\hat{x}$ 을 얻을 수 있습니다. 이때 기존의 reconstruction error 기반의 anomaly score는 다음과 같이 정의 될 수 있습니다.

\[\begin{aligned} \text{score}(x)&=||f\circ{g}(x)-x||_2 \\ &=||\hat{x}-x||_2 \end{aligned}\]

이때 인코더 내부의 $i$ 번째 레이어 $g_i$ 의 결과값을 $h_i$ 라고 하겠습니다.

\[h_i=g_{1:i}(x)\]

RaPP는 여기서 $\hat{x}$ 을 다시 인코더에 통과시킵니다. 이때 마찬가지로 인코더 내부의 각 레이어의 결과값을 구할 수 있을 것입니다. $i$ 번째 레이어의 그것을 $\hat{h}_i$ 라고 하겠습니다.

\[\begin{aligned} \hat{h}_i&=g_{1:i}(\hat{x}) \\ &=g_{1:i}\circ{f}\circ{g}(x) \end{aligned}\]

그럼 RaPP는 다음과 같이 $h_i$ 과 $\hat{h}_i$ 들의 concatenation 한 결과 벡터 사이의 distance로 정의됩니다.

\[\text{RaPP}(x)=\Big|\Big|[h_1;\cdots;h_\ell]-[\hat{h}_1;\cdots;\hat{h}_\ell]\Big|\Big|\]

여기서 경우에 따라 L2 Norm 또는 mahalanobis distance를 distance metric으로 사용합니다.

Motivation

RaPP는 굉장히 단순한 방법으로 anomaly score metric의 성능을 향상 시킵니다. 기존 복원 오차(reconstruction error) 기반의 이상탐지 기법은 보통 잘 동작하지만 가끔 아래와 같은 상황을 맞이할 수 있습니다.

아래의 예제는 MNIST에서 실제 오토인코더를 활용하여 reconstruction error 기반의 이상탐지를 수행할 경우 겪게 되는 현상입니다. ‘1’을 novelty class로 설정하고, 나머지 9개의 숫자들을 학습데이터로 삼아 학습하였을 때, 테스트 과정에서 오토인코더는 학습 과정에서 보지 못했던 ‘1’ 클래스의 샘플들을 성공적으로 복원해냅니다. 심지어 아래의 그림에 따르면 학습에서 보았던 클래스에 속하는 일부 샘플들보다도 복원 오차가 더 낮은 것을 볼 수 있습니다.

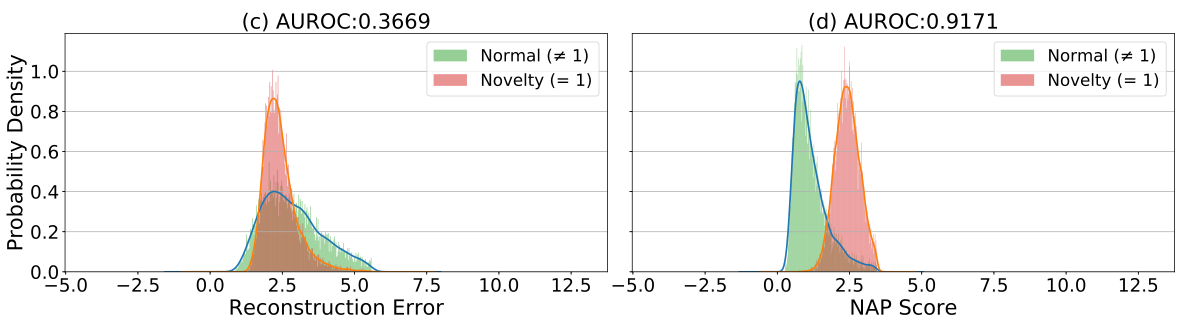
MNIST에서 '1'이 novelty class인 경우의 성능 저하 현상

이러한 경우에는 reconstruction error를 기준으로 anomalous sample을 탐지하는 전략이 실패합니다. 왼쪽 그림은 reconstruction error 기반의 novelty detection 결과이고, 0.37이라는 매우 낮은 AUROC 값을 보여줍니다. 심지어 0.5보다 낮은 것은 오히려 reconstruction error가 낮은 것을 선택하는 것이 더 나은 전략임을 말합니다. 아마도 우리는 ‘1’은 모양이 너무 단순하여, 다른 9개의 클래스로부터 학습된 특징(feature)들로 표현이 가능하기 때문에 복원이 잘 된 것이 아닐까 추측해볼 수 있습니다.

하지만 오른쪽의 RaPP의 NAP를 사용한 경우에는 성공적으로 novelty detection을 수행하는 것을 볼 수 있습니다. 이처럼 단순히 오토인코더의 입력과 출력을 비교하는 전략은 훌륭하지만 아쉬움이 여전이 남아있습니다. RaPP는 이때의 아쉬움을 달래고자, 양 끝의 데이터만 비교하는 방법을 좀 더 개선하고자 합니다.

만약 오토인코더의 입력과 출력만 비교하는 대신에, 인코더의 각 hidden layer의 출력값들과 디코더의 hidden layer의 출력값들을 비교하는 것은 어떨까요? 지난 포스팅에서 우리는 오토인코더의 인코더는 압축을 담당하고, 디코더는 압축의 복원(해제)을 담당한다고 이야기하였습니다. 그럼 압축 중간 과정 결과물과 복원 중간 과정의 결과물을 비교한다면, 기존의 입력/출력 값만을 비교하는 것에 비해서 훨씬 더 자세한 비교를 수행할 수 있지 않을까요?

인코더와 디코더의 대응되는 중간 레이어 결과값을 비교한다면?

하지만 아쉽게도 이 방법은 기존의 방법에서는 쉽지 않습니다. 우선 오토인코더는 입력과 출력의 차이만을 최소화하도록 학습되었기 때문입니다. — 그리고 그전에 오토인코더가 당연히 대칭의 구조를 가지고 있어야겠지요.

\[\mathcal{L}(\theta)=\sum_{i=1}^{N}{||x_i-A_\theta(x_i)||}\]

따라서 딥러닝의 학습 과정에서 신경망은 입력 $x_i$ 와 출력 $A(x_i)$ 에 대해서만 신경쓸 뿐, 인코더와 디코더의 중간 레이어의 출력값들은 신경쓰지 않습니다. “모로 가든 서울로 가면 된다”고 중간 레이어에서 어떤 값이 나왔던간에, 디코더의 최종 출력값이 입력값과 비슷하기만 하면 됩니다. 즉, 중간 결과값에 대한 어떠한 제약도 objective function(목적함수)에 없기 때문에, 중간 결과값끼리의 비교는 무의미합니다.

Methodology

하지만 RaPP는 단순한 방법을 통해, 앞서 언급한 인코더의 중간 레이어 결과값과 디코더의 중간 레이어 결과값을 비교하는 작업을 수행합니다.

인코더와 디코더가 각각 $\ell$ 개의 레이어를 갖는 오토인코더 $A$ 에 입력값 $x$ 를 넣어 얻은 출력값 $\hat{x}=A(x)$ 을 다시 인코더 $g$ 에 통과시킵니다. 이때 얻어지는 인코더의 중간 레이어 결과값을 앞서 $x$ 를 인코더에 통과시켰을 때의 중간 레이어 결과값과 비교합니다.

\[\text{RaPP}(x)=\sum_{i=0}^{\ell}{||g_{:i}(x)-g_{:i}\circ{A}(x)||}\]

위의 수식을 해석해 보면, 입력 샘플 $x$ 가 주어졌을 때, 인코더 $g$ 의 $i$ 번째 레이어까지의 결과값 $g_{:i}(x)$ 에, 오토인코더를 한번 통과시킨 값 $A(x)$ 을 다시 인코더 $i$ 번째 레이어까지 통과시켜 얻은 값 $g_{:i}\circ{A}(x)$ 을 비교하는 것을 볼 수 있습니다. 그리고 이 작업을 인코더의 전체 레이어에 대해서 각각 수행하여 모두 더하는 것을 볼 수 있습니다. — 이에 우리는 하나의 scalar 값을 얻게 되어 anomaly score로 사용 가능합니다.

위의 방법이 RaPP SAP(Simple Aggregation along Pathway)입니다. 하지만 이 경우에는 각 레이어들의 차이값들을 단순히 더하는데서 아쉬움이 남아있을 수 있습니다. 즉, SAP의 경우에는 아래의 그림에서 왼쪽과 같이 분포가 있을 때, 단순히 원점으로부터의 거리를 구하는 것이라고 볼 수 있습니다.

분포와 샘플이 주어졌을 때, Mahalanobis Distance의 개념

하지만 우리는 오른쪽과 같이 분포를 고려한 거리를 계산할 수 있습니다. 이는 Mahalanobis Distance와 같은 개념이라고 볼 수 있습니다. 이를 위해서 우리는 학습 샘플들의 각 레이어별 차이값에 SVD를 활용하여 normalized distance를 구할 수 있을 것입니다. 이 방법을 RaPP NAP(Normalized Aggregation along Pathway)라고 합니다.

결과적으로 SAP와 NAP를 통해서 우리는 여러 레이어로부터의 차이값들을 하나의 scalar값으로 만들어낼 수 있고, 이를 anomaly score로 활용하여 더 나은 이상탐지를 수행할 수 있습니다.

Intuitive Explanation

그럼 논문에서 다루지 못했던 이 알고리즘의 배경에 대해서 다소 추상적일 수 있으나 좀 더 이야기 해보겠습니다. — ICLR은 페이퍼를 8장으로 제한하고, 더 많은 장수를 사용할경우 추가 비용을 지불해야합니다.

오토인코더의 각 레이어들은 샘플로부터 (샘플을 복원하기 위한) 특징(feature)들을 추출해냅니다. 이 과정에서 복원하는데 필요하지 않은 정보들은 버려집니다. 학습된 특징들은 학습 데이터 내에서 샘플들을 구분하기 위해 필요한 정보들로 구성되어 있습니다. 만약 학습 데이터가 MNIST의 전체 숫자들을 담고 있었다면, 10가지의 숫자들을 구분하기 위한 특징들부터 우선적으로 학습될 것입니다. 만약 학습 데이터가 1가지의 숫자들로만 구성되어 있었다면, 해당 클래스 내에서 샘플들을 구분하기 위한 정보(e.g. 굵기, 기울기 등)들이 학습될 것 같습니다.

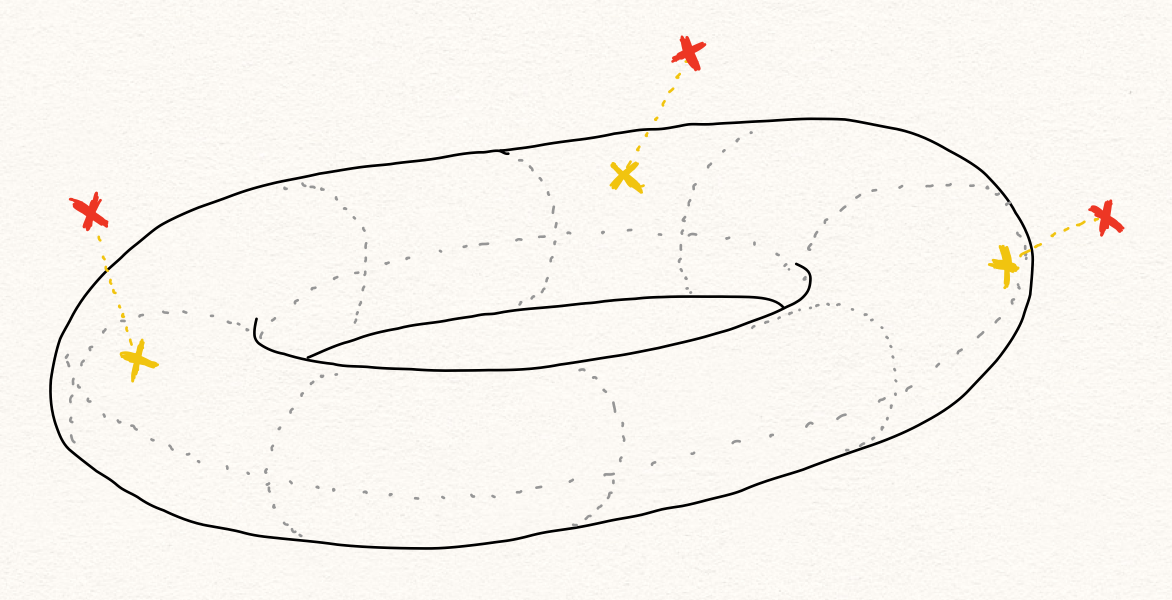
만약 비정상 샘플을 오토인코더에 통과시킨다면 어떻게 될까요? 비정상 샘플은 학습 과정에서 보지 못했던 특징(feature)들을 갖고 있을 것입니다. 이 특징들은 다른 기존의 샘플들과 구별할 수 있는 좋은 정보가 될 수 있으나, 학습 과정에서 미처 보지 못한 특징이기 때문에 아쉽게도 인코딩 과정에서 버려지게 됩니다. 결과적으로 비정상 샘플을 오토인코더에 통과시켜 복원된 값은 정상 데이터들로 학습된 특징들로만 구성되어 있을겁니다. 그럼 정상 데이터들의 특징들로만 구성된 데이터를 우리는 정상 데이터라고 부를 수 있지 않을까요? 즉, 어떤 데이터이든간에 오토인코더를 통과한 출력값은 정상 데이터의 범주에 속한다고 말할 수 있습니다.

다른 관점에서 이야기 해보겠습니다. 먼저 우리는 앞선 포스팅에서 오토인코더에 샘플을 통과시키는 작업은 학습 데이터를 통해 구성된 더 낮은 차원의 다양체에 샘플을 projection 하는 것이라고 이야기하였습니다. [2] 이 다양체는 매니폴드라고 불리우며, 정상 데이터들로만 구성되어 있습니다. 즉, 일반적으로 샘플은 noise를 가지고 있고, 오토인코더를 통과시키는 과정은 이 noise를 제거하는 과정(매니폴드에 projection하는 과정)이라고 볼 수 있습니다. 따라서 이 noise의 크기가 큰 경우에는 비정상 데이터라고 간주하는 것입니다. 결론적으로 우리는 “오토인코더의 결과값은 매니폴드 위에 존재하며 정상에 속한다”라고 이야기 할 수 있습니다.

정상 샘플을 오토인코더에 통과시킨 출력값을 다시 인코더에 넣어 압축하면 어떻게 될까요? 이상적으로 보았을 때, 오토인코더의 출력값은 인코더로부터 추출된 특징들로만 이루어져 있기 때문에 인코딩 과정에서 버려지는 정보는 없을 것입니다. 즉 다르게 표현하면, 인코더의 중간 레이어들이 표현하는 공간에 존재하는 각 매니폴드 위에 항상 존재할 것입니다. (또 다른 표현으로는, $\hat{x}$ 를 인코더의 각 레이어에 통과시키는 것은, 각 레이어 출력값들이 존재하는 공간에 $\hat{x}$ 를 translation 한 것이라고 볼 수 있습니다.) 이에 반해 처음 인코더를 통과하는 값은 아직 매니폴드 위에 존재하지 않습니다. 따라서 우리는 이 두 값의 차이를 계산할 수 있는 것입니다.

인코더를 통과하면서 RaPP의 계산이 이루어지는 과정

다시한번 이야기하면, 오토인코더를 통과하여 복원된 값은 정상 데이터에 속하며, 그 정상 데이터를 이루는 특징들은 학습 데이터로부터 학습된 것입니다. 그럼 만약 비정상 데이터를 오토인코더에 통과시키면 어떻게 될까요? 그럼 오토인코더를 통과한 비정상 데이터는 정상 데이터들로 구성된 매니폴드에 projection 될 것이고, 정상 데이터들의 특징들로만 구성된 나름의 정상 데이터가 됩니다. 이 값을 이제 다시 인코더에 넣으면 어떻게 될까요? 여전히 중간 레이어 결과값은 각 공간의 매니폴드 위에 존재할 것입니다. 그럼 마찬가지로 인코더를 처음 통과할 때의 중간 결과값과 비교하면 됩니다.

Equations

이미 학습된 오토인코더 $A=f\circ{g}$ 가 있을 때, 매니폴드 $M_0$ 은 다음과 같이 정의 할 수 있습니다. [3]

\[\forall{x}\in{M_0}\text{, }x=A(x)\text{ where }M_0=\{A(x):x\in\mathbb{R}^n\}.\]

이것은 입력 데이터가 존재하는 공간(space)에 정의된 매니폴드라고 볼 수 있고, 마찬가지로 $i$ 번째 레이어의 결과값들이 존재하는 공간에도 매니폴드가 정의될 수 있을 것입니다.

\[M_i=\{g_{:i}(x):x\in{M_0}\}\]

이러한 관점에서 $g$ 와 $f$ 는 $M_0$ 과 $M_\ell$ 사이의 맵핑 함수이며 서로 역함수 관계라고 볼 수 있습니다.

이때 가상의 디코더 함수 $\tilde{f}$ 가 존재한다고 해보겠습니다.

\[\begin{gathered} \tilde{f}=\tilde{f}_1\circ\cdots\circ\tilde{f}_\ell \\ \forall{x}\in{M_\ell}\text{, }\tilde{f}(x)=f(x). \end{gathered}\]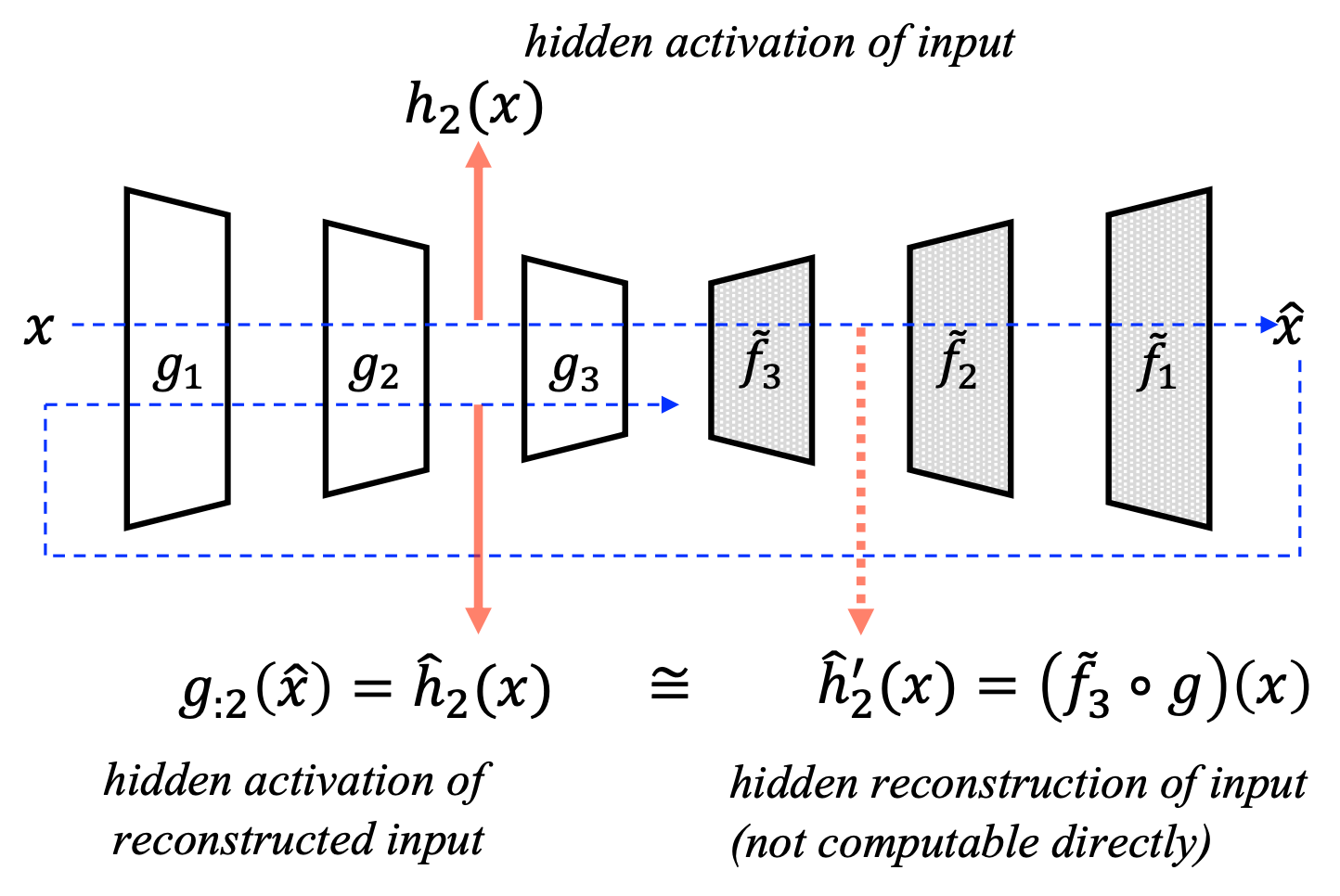

수식에 따라서 우리는 RaPP를 통해 가상의 디코더에 대한 중간 레이어 결과값을 얻을 수 있습니다.

그리고 이 디코더 $\tilde{f}$ 는 인코더 $g$ 와 대칭대는 구조를 지녔으며, 이 가상 디코더의 각 레이어는 인코더의 대응되는 레이어의 역함수라고 가정해보겠습니다.

\[\forall{a}\in{M_i}\text{, }a=(g_i\circ\tilde{f}_i)(a).\]

이런 디코더가 있다면 우리는 디코더 중간 레이어의 중간 레이어 결과값을 인코더의 중간 레이어 결과값에 바로 비교 가능할 것입니다. 즉, 이 디코더의 중간 레이어 결과값을 아래와 같이 $\tilde{h}{i}(x)$ 라고 정의할 때, 우리는 이 $\tilde{h}{i}(x)$ 와 $g_{:i}(x)$ 를 비교하면 됩니다.

\[\begin{gathered} \text{RaPP}(x)=\sum_{i=0}^{\ell}{||g_{:i}(x)-\tilde{h}_i(x)||}\text{,} \\ \text{where }\tilde{h}_i(x)=\tilde{f}_{\ell:i+1}\circ{g}(x). \end{gathered}\]

그런데 알고보면 $\tilde{h}_{i}(x)$ 는 아래와 같이 전개할 수 있습니다.

\[\begin{aligned} \forall{x}\in\mathbb{R}^n\text{, }\tilde{h}_i(x)&=\tilde{f}_{\ell:i+1}\circ{g}(x) \\ &=(g_{:i}\circ{\tilde{f}_{i:1}})\circ{\tilde{f}_{\ell:i+1}}\circ{g}(x)\text{, because }g(x)\in{M_\ell}\\ &=g_{:i}\circ{\tilde{f}}\circ{g}(x) \\ &=g_{:i}\circ{f}\circ{g}(x)\text{, because }\tilde{f}(x)=f(x)\text{, }\forall{x}\in{M_\ell} \\ &=g_{:i}\circ{A}(x) \\ &=g_{:i}(\hat{x})\text{, where }\hat{x}=A(x)\in{M_0}. \end{aligned}\]

위와 같이 $\tilde{h}{i}(x)$ 는 $g(\hat{x})$ 와 같음(equivalent)을 알 수 있습니다. 따라서 RaPP는 아래와 같이 정의 됩니다.

\[\begin{aligned} \text{RaPP}(x)&=\sum_{i=0}^{\ell}{||g_{:i}(x)-\tilde{h}_i(x)||} \\ &=\sum_{i=0}^{\ell}{||g_{:i}(x)-g_{:i}(\hat{x})||} \end{aligned}\]

Experiments

우리는 다양한 실험을 통해 RaPP를 검증하고자 하였습니다. 먼저 MNIST와 FMNIST 같은 널리 알려진 데이터셋을 통해서 기존에 출판된 논문들의 성능과 비교하는 작업을 거치고, 마키나락스가 주로 타겟하고 있는 tabular 데이터셋에 대해서도 실험을 수행하였습니다. 벤치마크 데이터셋에 대해서 실험을 수행한 결과는 아래와 같습니다.

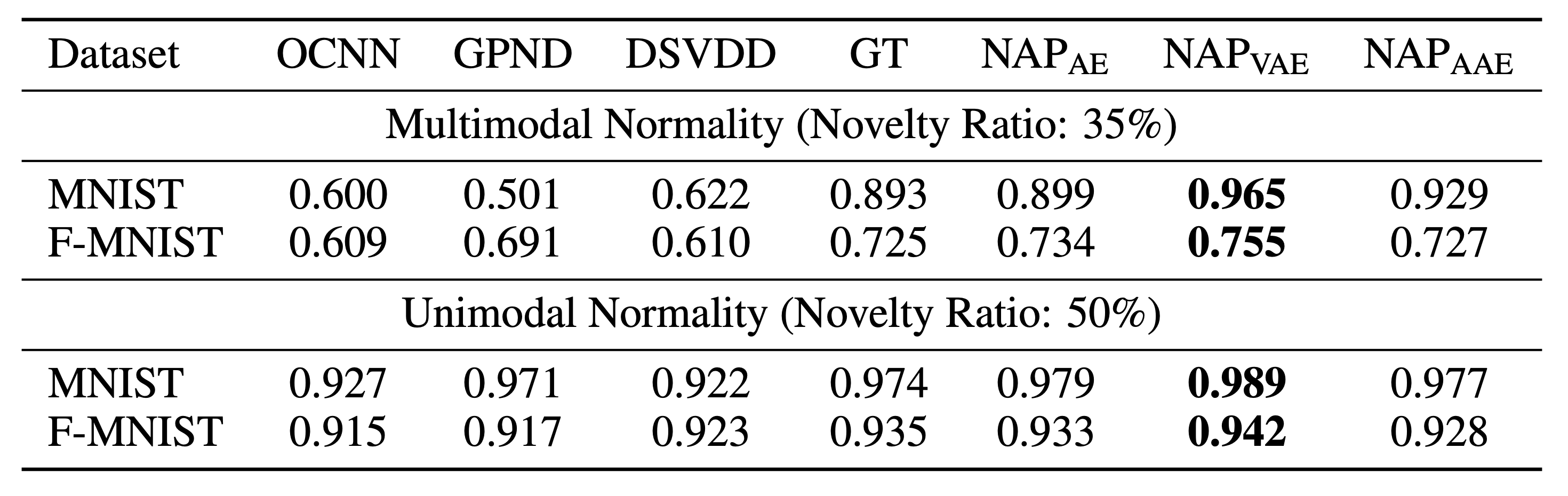
MNIST와 FMNIST에 대한 실험 결과

결과에서 볼 수 있듯이, 다양한 오토인코더(AE, VAE[4], AAE[5])에 NAP를 적용하였을 때, 기존에 출판된 논문(OCNN[6], GPND[3], DSVDD[7], GT[8])들보다 더 뛰어난 성능을 보이는 것을 확인할 수 있었습니다. 특히 VAE에 NAP를 적용하였을 떄가 가장 뛰어난 성능을 보였습니다. 또한, OCNN, GPND, DSVDD와 같이 One Class Classification 문제로 정의한 알고리즘들은 아쉽게도 multimodal normality 케이스에서 제대로 동작하지 못하는 것을 확인할 수 있습니다.

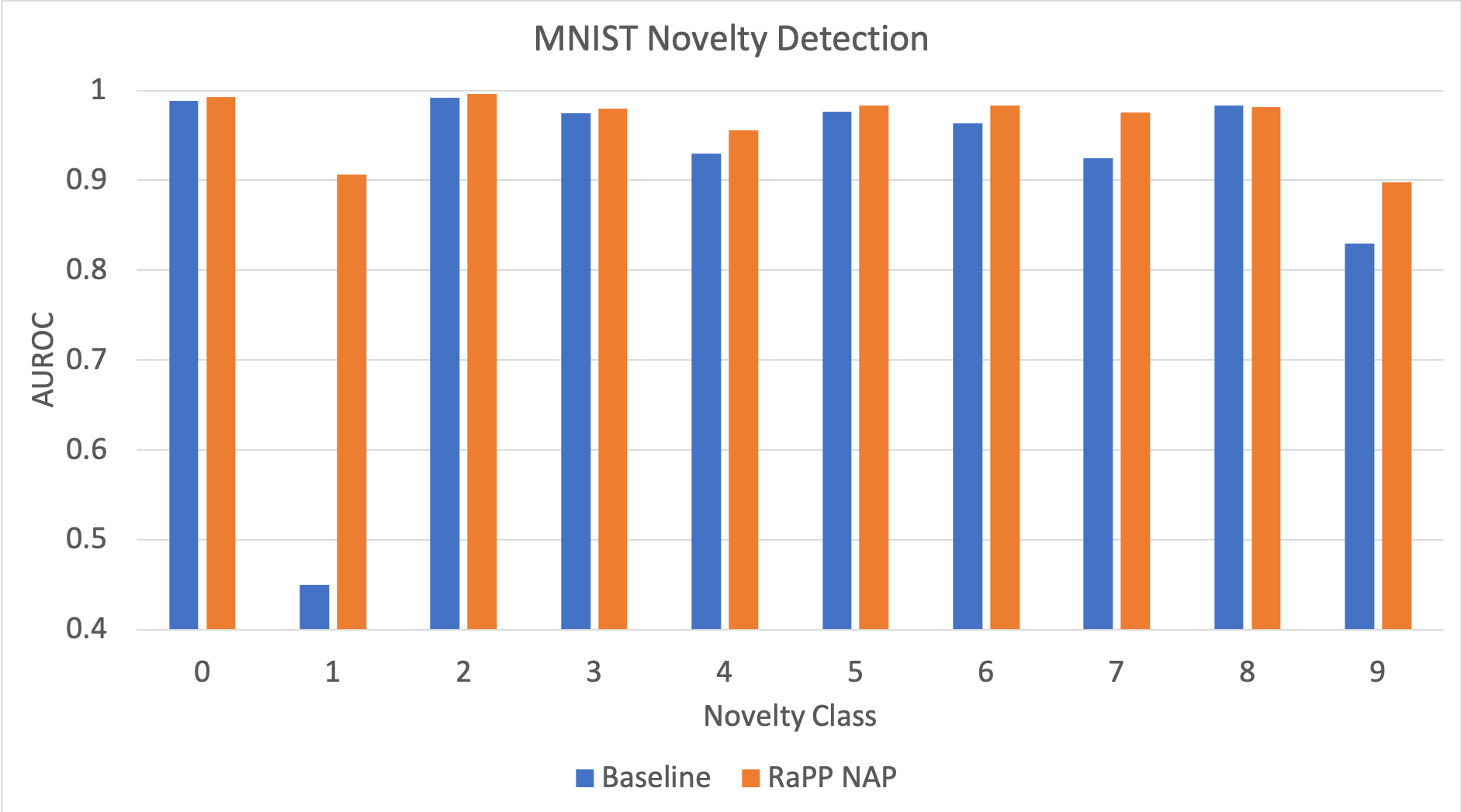
또한 아래와 같이 multimodal normality 케이스에 대해서 각 클래스 별로 살펴보았을 때, 기존 대비 RaPP가 (‘1’에서의 큰 성능 향상을 포함하여) 대부분의 클래스에서 성능을 높이는 것을 확인할 수 있습니다. 자세한 실험 셋팅은 논문을 참고바랍니다.

MNIST 클래스별 AUROC

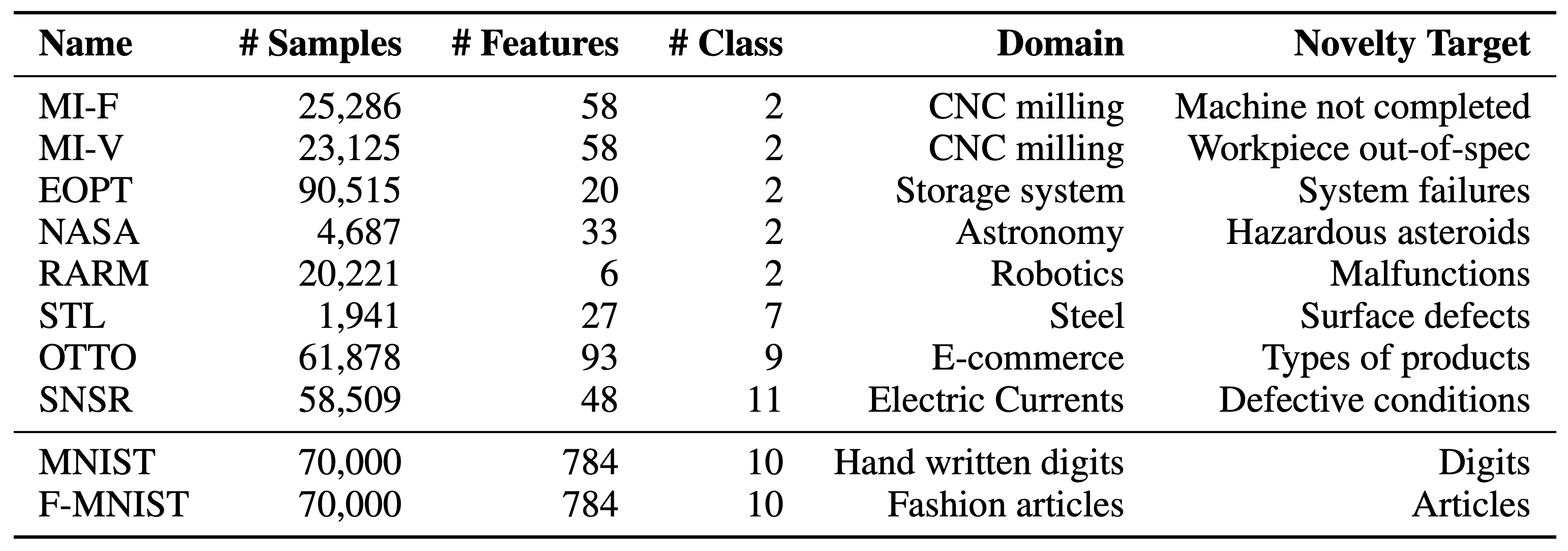
MNIST와 같은 이미지 데이터들은 tabular 데이터셋과 양상이 다를 수 있기 때문에, tabular 데이터셋에 대해서도 RaPP를 실험하였습니다. 이때는 기존에 출판된 논문들이 tabular 데이터셋에 대해서 성능을 제공하지 않았을 뿐더러, 대부분 convolutional layer를 사용한 상태이므로 적용하기가 힘들었습니다. 따라서 기존의 오토인코더와 RaPP를 적용한 결과를 비교하여, RaPP의 적용에 따른 성능 향상을 실험하고자 하였습니다. 우선 실험에 사용된 tabular 데이터셋은 아래와 같이 구성되어 있습니다.

Tabular 데이터셋에 대한 설명

나중에 보니 STL(steel) 데이터셋은 워낙 클래스당 샘플 수가 적어서 train/valid/test random split에 따라 굉장히 편차가 심한 결과를 보여주었습니다.

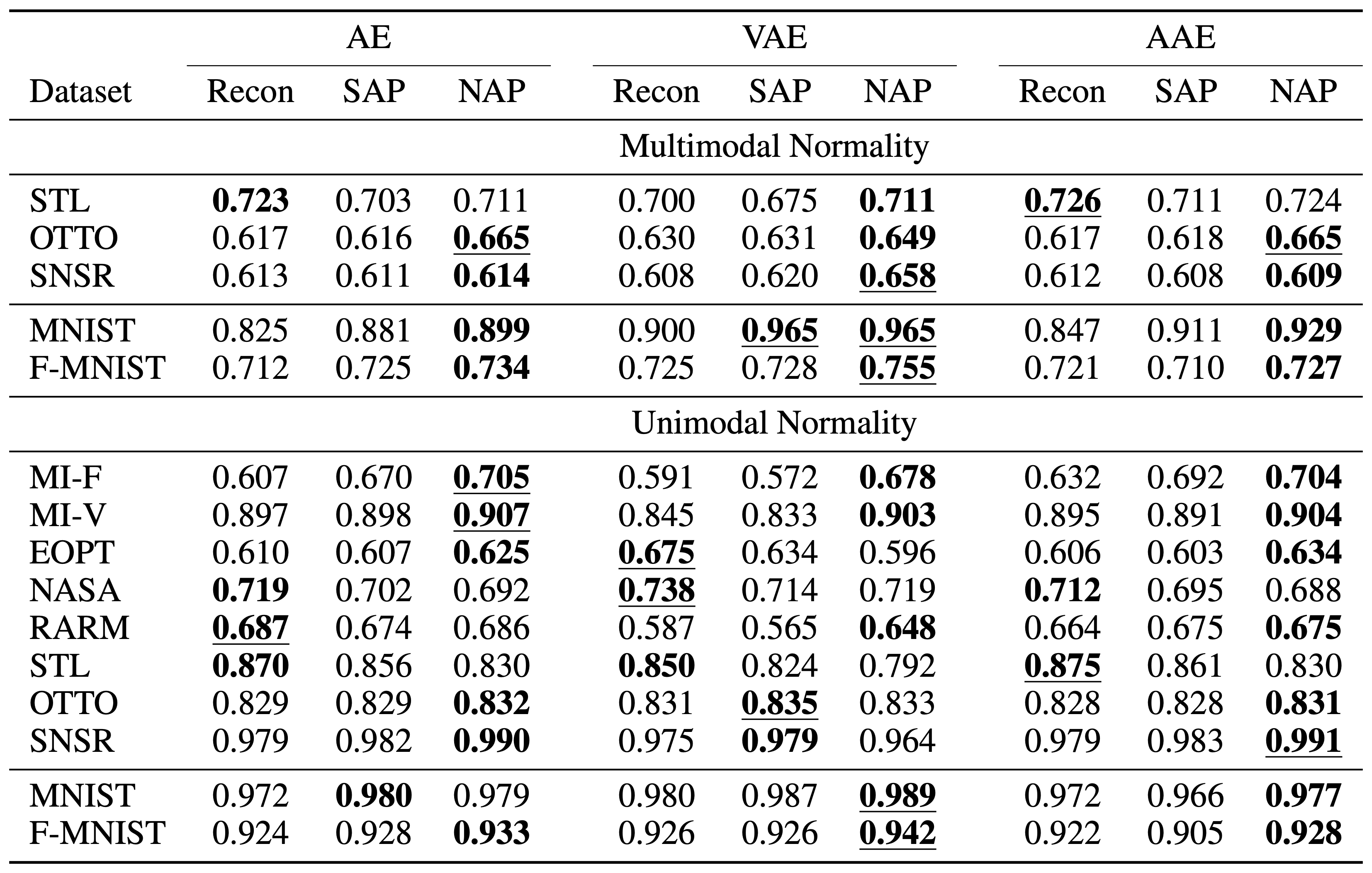
Tabular 데이터셋에 대한 실험 결과

실험 결과에 따르면, RaPP는 multimodal normality 케이스에서 더 뛰어난 모습을 보여줍니다. Multimodal normality 케이스에서는 STL을 제외하고 모든 데이터셋에서 RaPP를 통해 성능을 향상할 수 있었습니다. 반면에 Unimodal normality 케이스에서는 총 10가지 경우 중에서 6가지 경우에 RaPP가 뛰어난 모습을 보여줍니다. 다만, 대부분의 tabular 데이터셋은 시계열 데이터셋인데 반해, 이 실험에서는 RaPP를 적용할 때 iid로 가정하고 적용하였습니다. – 시계열 데이터셋의 경우에는 RNN과 같은 모델을 활용하지 않더라도 윈도잉과 같은 기법을 통해 시계열의 성질을 어느정도 반영할 수 있습니다.

Discussion & Conclusion

재미있게도 MNIST와 FMNIST의 실험결과를 보면 기존의 anomaly detection 논문들의 성능이 reconstruction error 기반의 baseline anomaly detection 성능보다도 낮은 것을 볼 수 있습니다. 이것은 AE를 비롯한 VAE, AAE에 대한 정확한 구현과 실험 및 검증이 원활하게 이루어지지 않은것이 아닌가 생각해볼 수 있습니다. 실제로 앞서 포스팅에서 언급한대로 주류 연구 분야가 아니다보니 생기는 문제로 생각해볼 수 있으며, 제대로 된 벤치마크 성능의 부재는 연구를 진행하며 느꼈던 큰 아쉬움 점이기도 합니다.

따라서 RaPP를 실험할 때에는 Unimodal/Multimodal Normality 케이스로 나누어 실험을 진행하였으며, MNIST와 FMNIST 이외에도 다양한 tabular 데이터셋에 대해서도 anomaly detection 실험을 수행하였습니다. 하지만 워낙 다양한 실험을 진행하다보니 아쉽게도 다양한 케이스에 대해서 최적의 성능을 뽑아내진 못하였으며, 페이퍼에 기재된 성능은 아직 upper bound에 대해서 margin이 남아 있습니다.

MNIST와 FMNIST 같은 이미지 데이터셋을 비롯하여, 페이퍼 상의 모든 실험들은 fully-connected layer를 활용한 오토인코더들로 구현되었습니다. 아쉽게도 RaPP 알고리즘을 바로 Convolutional Layer에 적용하는 것은 아직 연구가 필요한 부분입니다.

이번 포스팅에서는 마키나락스에서 ICLR에 출판한 논문인 RaPP에 대해서 살펴보았습니다. 논문이라는 제약 때문에 미처 페이퍼에서는 다루지 못했던 내용들과 함께, 전반적인 내용들을 보다 쉽게 풀어서 설명하고자 하였습니다.

요약하자면 RaPP는 기존의 훈련방식을 통해 학습된 오토인코더에서 더 나은 anomaly score를 구하는 방법을 제안한 것이라고 볼 수 있습니다. 특히 NAP 방식을 통해서 우리는 여러가지 데이터셋에서 더 높은 성능의 anomaly detection을 수행할 수 있었습니다. 결과적으로 RaPP는 목적함수의 수정이 없이 성능을 개선했다는 장점이 있으나, NAP의 계산과정이 무겁다는 단점이 존재합니다. – 이에 대해서는 Appendix A에서 다루고 있습니다.

References

[1] Ki Hyun Kim et al., Rapp: Novelty Detection with Reconstruction along Projection Pathway, ICLR, 2020
[2] Lei et al., Geometric Understanding of Deep Learning, Arxiv, 2018
[3] Stanislav Pidhorskyi et al., Generative Probabilistic Novelty Detection with Adversarial Autoencoders, NeurIPS, 2018
[4] Kingma et al., Auto-Encoding Variational Bayes, ICLR, 2014
[5] Makhzani et al., Adversarial autoencoders. Arxiv, 2015.
[6] Raghavendra Chalapathy et al., Anomaly detection using one-class neural networks. arXiv preprint arXiv:1802.06360, 2018.
[7] Lukas Ruff et al., Deep one-class classification. In ICML, 2018.
[8] Izhak Golan and Ran El-Yaniv. Deep anomaly detection using geometric transformations. NIPS, 2018.
[9] Ki Hyun Kim, Operational AI: Building a Lifelong Learning Anomaly Detection System, DEVIEW, 2019

Autoencoder based Anomaly Detection

이번 포스팅에서는 오토인코더 기반의 이상탐지(anomaly detection)에 대해서 살펴보도록 하겠습니다. 오토인코더는 입력을 그대로 출력(복원)해내도록 하는 목적 함수를 갖습니다. 따라서 보통 MSE 손실 함수를 사용하며, 중간에 bottle-neck(병목)이 있어 고차원 공간 상의 입력 데이터를 저차원의 공간으로 맵핑(mapping)하여 잠재적인 변수로 표현(latent representation)하였다가, 다시 입력과 같은 고차원의 공간으로 복원해내야 합니다.

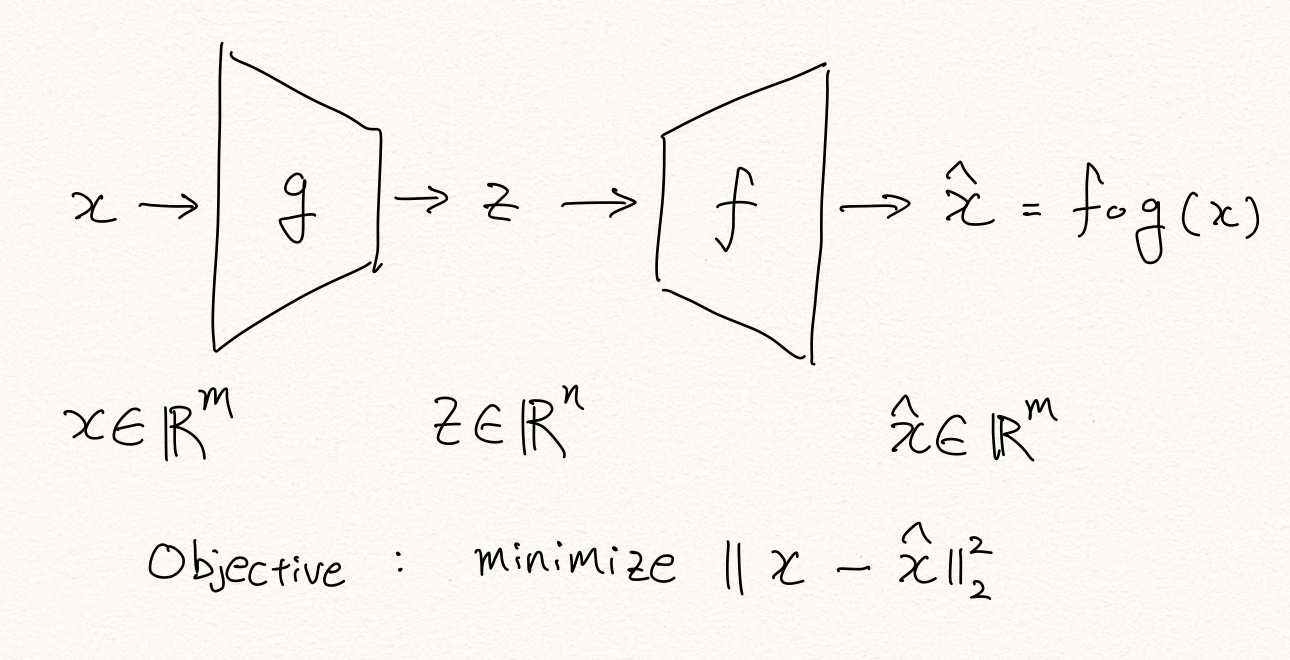
오토인코더의 동작 예

여기서 인코더와 디코더는 여러개의 non-linear 계층을 가질 수 있으며, non-linear activation function을 없애서 linear한 형태로 오토인코더를 구성할 경우 PCA 처럼 동작하게 됩니다.

Anomaly Detection with AE

오토인코더를 활용하여 이상탐지를 수행하는 과정은 다음과 같습니다.

입력 샘플을 인코더를 통해 저차원으로 압축합니다.
압축된 샘플을 디코더를 통과시켜 다시 원래의 차원으로 복원합니다.
입력 샘플과 복원 샘플의 복원 오차(reconstruction error)를 구합니다.
복원 오차는 이상 점수(anomaly score)가 되어 threshold와 비교를 통해 이상 여부를 결정합니다.
- threshold 보다 클 경우 이상으로 간주
- threshold 보다 작을 경우 정상으로 간주

위의 과정에서 오토인코더는 복원 오차를 최소화하기 위해서 병목 구간을 지날 때, 최소한의 정보량을 잃기 위해 자동으로 학습될 것입니다. 즉, MNIST의 예로 들면, 주변부의 항상 숫자가 존재하지 않는 뻔한 pixel들은 굳이 기억하지 않아도 될 것이고, 중간 pixel들을 좀 더 효율적으로 기억하도록 할 것입니다.

그럼 비정상 샘플이 테스트 과정에서 주어질 경우, 오토인코더는 주어진 샘플에 대해서 효과적으로 압축과 복원을 수행하지 못할 것입니다. 결국 주어진 샘플들의 특징을 잘 추출해내지 못할 것이므로, 복원 오차(reconstruction error)는 커질것이므로 비정상 샘플로 판별할 수 있습니다.

하지만 때때로 표현에 필요한 최적의 병목 구간 크기에 비해서 실제 병목 구간의 크기가 너무 클 경우(극단적인 경우에는 입력 샘플과 크기가 같을수도), 오토인코더는 identity function이 되어 입력을 그대로 복사해내는 능력을 갖게 될 것입니다. 즉, 학습 과정에서 보지 못했던 비정상 샘플이 주어져도 그냥 그대로 복사해버리는 능력을 가질 수 있습니다. 따라서 우리는 병목 구간의 크기를 하이퍼 파라미터(hyper-parameter)로써 적절하게 잘 조절할 필요성이 있습니다.

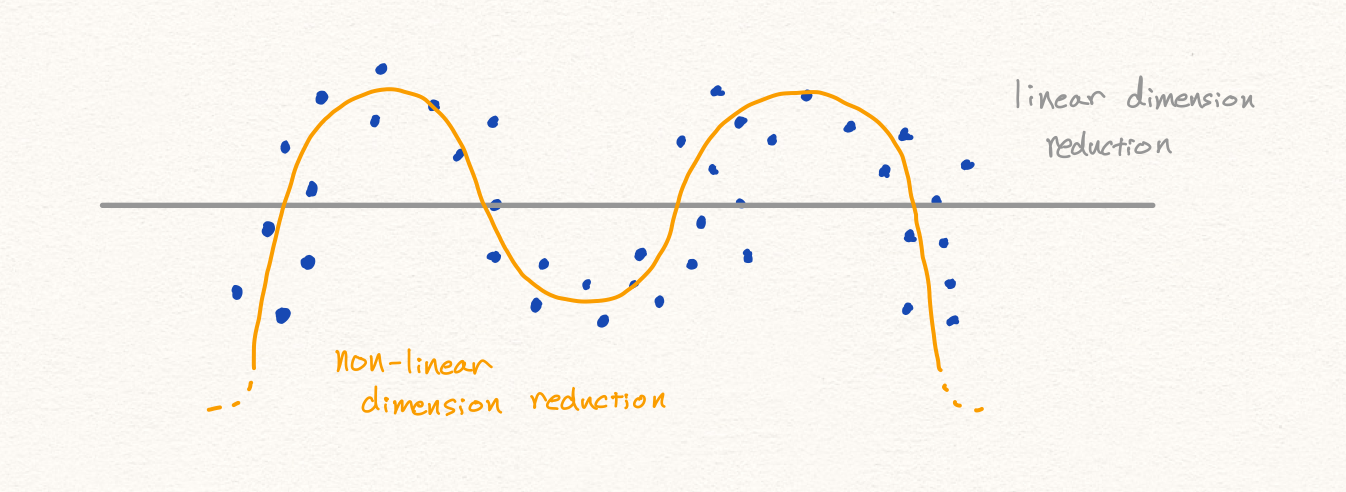
Nonlinear Dimension Reduction (AE)

오토인코더도 차원 축소를 통해 특징(feature)을 추출 하는 방법을 학습합니다. 다만 비선형적인 차원 축소를 다룬다는 점에서 PCA와 큰 차이점을 지닙니다. 하지만 차원 축소를 다룬다는 점에서 여러가지 생각할 점들이 많습니다.

Manifold Hypothesis

먼저 우리는 매니폴드(Manifold) 가설 관점에서 생각해 볼 수 있습니다. 아래의 수식 및 설명은 NIPS 2018에서 발표된 GPND(Generative Probabilistic Novelty Detection with Adversarial Autoencoders) [1] 에서 제시한 방법으로 매니폴드와 오토인코더의 관계를 잘 설명해 줍니다.

매니폴드와 오토인코더의 관계 -- 출처: GPND

위의 설명에 따르면 우리에게 주어진 데이터 샘플 $x$ 는 매니폴드 $f(z)$ 에 노이즈 $\xi$ 가 더해진 형태가 됩니다.

\[x=f(z)+\xi\]

이때 저차원 공간에서 고차원 공간으로의 맵핑 함수 $f$ 에 의해서 정의된 매니폴드 $\mathcal{M}$ 에 $f(z)$ 가 속하는 것을 알 수 있습니다. 그리고 저차원의 $z$ 가 속하는 공간 $\Omega$ 가 정상 데이터들의 집합임을 알 수 있습니다. 즉, 인코더를 통과시키는 과정은 고차원에서 저차원으로의 맵핑 과정일 뿐만 아니라 노이즈 $\xi$ 를 제거하는 작업(denoising)임을 알 수 있고, 이 노이즈의 크기에 따라서 정상이냐 비정상이냐를 결정하는 것이라고 생각해 볼 수 있을 것입니다.

빨간색 점이 매니폴드 표면의 노란색 점으로 투사된 예제

다르게 표현하면, 오토인코더에 샘플을 통과시키는 것은 매니폴드 표면 $\mathcal{M}$ 에 투사(projection)하는 과정[2]이라고 볼 수 있고, 이는 디노이징이라고 볼 수 있으며, 그 결과 복원 오차(reconstruction error)가 발생하는 것이라고 볼 수 있습니다.

Latent space

오토인코더는 학습 데이터 내에서 샘플을 잘 설명할 수 있는 특징(feature)을 추출해냅니다. 이것은 PCA에서 분산(variance)을 최대화 하는 방향으로 PC를 찾는 것과 비슷하다고 볼 수 있을 것입니다. 좁은 bottle-neck을 통과해야 하기 때문에, 정보량이 높은 특징들을 우선적으로 추출해 낼것 입니다. [3, 5, 6] 결과적으로 인코더의 레이어를 통과하면서 복원에 덜 필요한 특징들은 버려지게 됩니다. 즉, 각 레이어의 결과물들은 복원에 필요한 정보들이 남아있게 됩니다.

이러한 의미에서 이상적인 상황에서 잠재 공간(latent space)에 표현된 latent(or hidden) representation은 비정상 데이터에 대한 정보는 남아있지 않습니다. 즉, 비정상 데이터를 통과시키더라도, 정상 데이터와 다름을 알려줄 수 있는 (비정상 데이터에 대한) 정보는 남아있으리라는 보장이 없습니다.

Relationship between $P(x)$ and $P(z)$

해당 관점에서 $P(x)$ 가 낮은 샘플 $x$ 를 찾고자 하는 이상 탐지 문제에서 잠재 공간에서의 확률 분포 $P(z)$ 를 살펴보는 것은 큰 도움이 되지 않을 가능성이 높습니다. 흔히 비정상 샘플 $\tilde{x}$ 가 있을 때, 비정상 샘플은 정상 샘플 $x$ 와 비슷하지 않으므로 고차원의 공간 상에서 $P(x)$ 분포의 밀도가 낮은 곳에 위치할 가능성이 높다고 생각할 것입니다. 따라서 $\tilde{x}$ 의 인코딩 결과값 $\tilde{z}$ 의 확률값 $P(\tilde{z})$ , 또한 낮지 않을까 생각 할 수 있습니다.

하지만 앞서 서술한대로, latent space에는 학습 데이터를 잘 설명하기 위한 특징들만 정의되어 있기 때문에, 비정상 샘플 또한 정상 특징들로만 표현될 것입니다. 따라서 정상 특징들의 조합으로 이루어진 비정상 샘플의 hidden representation은 정상 샘플의 그것과 크게 다르다는 보장이 없습니다. 따라서 $P(z)$ 를 활용하여 $P(x)$ 가 낮은 것을 판별하는 것은 쉽지 않은 일이 될 것 입니다.

$P(z)$ 를 보는 것은 unimodal normality case를 가정한 문제 정의 아래에서는 괜찮은 접근 방법일 수 있습니다. 정상 데이터의 패턴이 크게는 하나라고 볼 수 있기 때문에, $P(x)$ 를 gaussian distribution 형태의 $P(z)$ 로 mapping 할 수 있고, 이때에는 $P(x)\varpropto{P(z)}$ 라고 가정하는 것은 가능합니다. 따라서 위의 unimodal normality case 가정을 따른 논문들은 $P(z)$ 를 anomaly score를 구하는데 사용합니다. [1] 하지만 아래의 그림과 같이 이런 가정은 multimodal normality case에서는 동작하지 않을 수 있습니다.

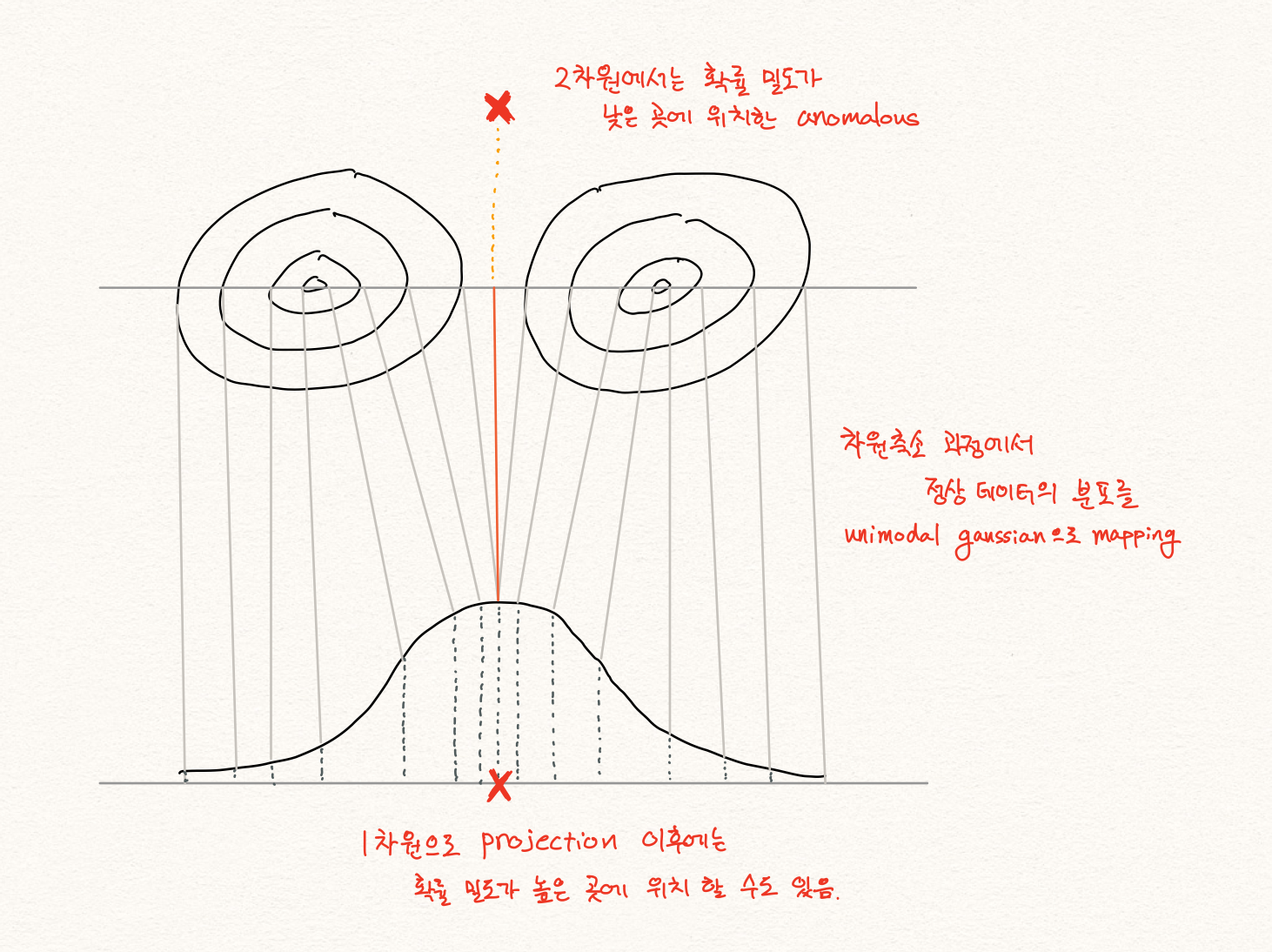
P(z) 를 gaussian distribution으로 가정하면 확률 밀도 값을 쉽게 구할 수 있지만, multimodal normality case에서 동작하지 않을 수 있습니다.

다른 관점에서 $P(x)\varpropto{P(z)}$ 에 대한 간단한 반례에 대해 생각해 볼 수 있습니다. 우리는 기본적으로 복원 오차(reconstruction error)를 활용하여 anomaly score를 구합니다.

만약 우리에게 정상 샘플 $x$ 가 있고, 이를 복원한 샘플 $\hat{x}$ 이 있다고 해보겠습니다. 이때 비정상 샘플 $\tilde{x}$ 가 주어졌고, 우연히 복원한 결과 똑같은 아까와 똑같은 복원 샘플 $\hat{x}$ 을 얻었다고 해보겠습니다. 여기서 우리의 오토인코더는 매우 뛰어나게 잘 동작했기 때문에 $||x-\hat{x}||=0$ 이라는 결과를 얻었다고 합시다. 그럼 $||x-\hat{x}||\ll||\tilde{x}-\hat{x}||$ 이 성립할 것입니다.

결과적으로 디코더가 저차원에서 고차원으로 가는 1:1 함수라고 가정한다면(현실은 ReLU를 사용한다면 다대일 함수일 가능성이 높습니다.), 인코더 함수 $f$ 에 대해서 $f(x)=f(\tilde{x})$ 라고 볼 수 있고, 이는 latent space에서 $P(z)$ 가 낮은지 확인하는 것은 $P(x)$ 가 낮은것을 확인하는 것을 보장하지 않는 것임을 알 수 있습니다.

Variational Autoencoders

2014년 Kingma는 Auto-Encoding Variational Bayes [4]라는 논문을 통해 VAE(Variational Autoencoders)를 발표합니다. 이 논문에서 VAE는 reparameterization trick을 활용하여 인코더가 뱉어낸 분포의 파라미터( $\mu,\sigma$ )로부터 latent variable $z$ 를 샘플링하고, 이로부터 posterior distribution $p(x|z)$ 를 근사(approximate)합니다.

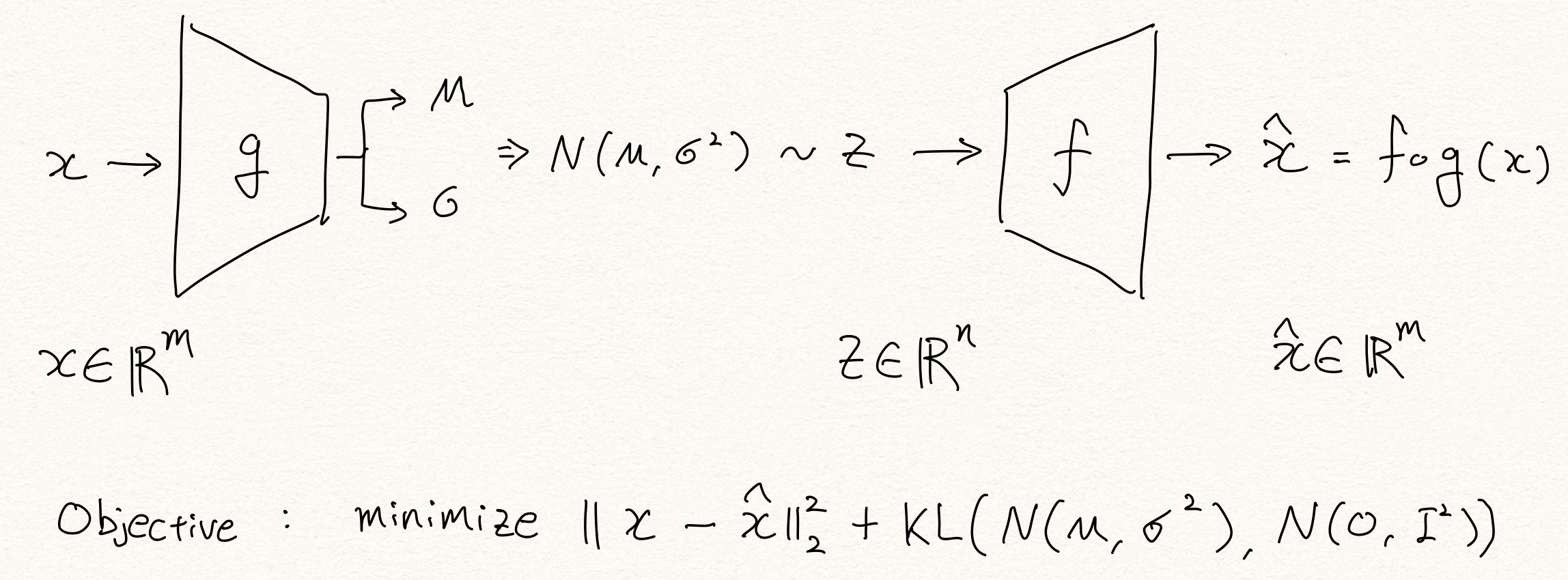
VAE의 동작 원리

이 과정에서 유도된 수식에 의해 KL-divergence 항이 추가 되어 regularization 역할을 수행합니다.

\[\log{p(x)}\ge\mathbb{E}_{\text{z}\sim{p(z|x;\theta)}}\big[\log{p(x|\text{z};\phi)}\big]-\text{KL}\big(p(\text{z}|x;\theta)||p(\text{z})\big)\]

Variational Information Bottleneck

이때 VAE의 KLD term은 이상 탐지에서 매우 훌륭한 역할을 수행합니다. Information bottleneck theory [3, 5, 6]는 심층신경망이 학습되는 원리에 대해서 설명하고자 하는 이론입니다. 오토인코더의 병목 구간과 같이 차원 축소의 과정에서 중요한 특징(feature)을 추출하는 방법이 자동으로 학습될 수 있다는 내용입니다. (사실 우리는 오토인코더가 아니더라도 보통 차원 축소가 되도록 신경망을 구성합니다.) 이 정보의 병목(information bottleneck)은 자연스럽게 각 레이어별로 mutual information이 최대화 되도록 하며, 이 과정에서 mutual information을 최대화 하는 것과 상관 없는 특징들은 자연스럽게 떨어져 나갑니다.

VAE의 흥미로운 점은 Variational Information Bottleneck (VIB) [7]을 제공한다는 점 입니다. 오토인코더(AE)는 물리적으로 레이어의 출력 유닛 갯수를 점차 줄여나가며 병목 구간에서 최종적인 information bottleneck을 걸게 되지만, VIB는 수식에 의해서 자연스럽게 가상의 information bottleneck을 갖게 됩니다.

VAE의 수식에는 KLD 항 $\text{KL}\big(p(\text{z}|x)||p(\text{z})\big)$ 이 있는데요, $\log{p(x)}$ 을 최대화 하기 위해서는 자연스럽게 KLD 항을 최소화 해야 합니다. 이 관점에서 KLD 항을 풀어보면 아래와 같습니다.

\[\begin{aligned} \text{KL}\big(p(\text{z}|x)||p(\text{z})\big)&=-\mathbb{E}_{\text{z}\sim{p(\text{z}|x)}}\bigg[\log{\frac{p(\text{z})}{p(\text{z}|x)}}\bigg] \\ &=\mathbb{E}_{\text{z}\sim{p(\text{z}|x)}}\bigg[\log{\frac{p(\text{z}|x)}{p(\text{z})}}\bigg] \\ &=\mathbb{E}_{\text{z}\sim{p(\text{z}|x)}}\bigg[\log{\frac{p(x,\text{z})}{p(x)\cdot{p(\text{z})}}}\bigg] \\ \end{aligned}\]

이때, 아래와 같이 mutual information (MI) 수식과 비교해볼 수 있습니다.

\[\begin{aligned} \text{I}(Z;X)&=\sum_{X\in\mathcal{X}}P(X)\sum_{Z\in\mathcal{Z}}P(Z|X)\log{\frac{P(X,Z)}{P(X)\cdot{P(Z)}}} \\ &=\mathbb{E}_{Z\sim{P(Z|X),X\sim{P(X)}}}\bigg[\log{\frac{P(X,Z)}{P(X)\cdot{P(Z)}}}\bigg] \end{aligned}\]

우리는 MI는 KLD와 매우 밀접한 관련이 있음을 알 수 있습니다. 즉, VAE에서 KLD 항을 최소화 하는 것은 $x$ 와 $z$ 사이의 MI를 최소화 하는 것과 같습니다. 여기서 MI가 만약 최소화되어 0이 된다는 것은 두 random variable이 독립이 된다는 것입니다.

결론적으로 VAE는 $\log{p(x)}$ 를 최대화 하는 과정에서, KLD를 최소화하려 할 것입니다. 이 과정에서 만약 극단적으로 KLD가 0이 된다면 $x$ 와 $z$ 는 독립이 될 것이므로, reconstruction error가 커질 것이고 $\log{p(x)}$ 를 최대화 하지 못할 것입니다. 따라서 적당히 $x$ 와 $z$ 의 MI를 유지하는 선에서 KLD를 최소화 하기 위해서, 복원(reconstruction)에 상관없는 특징 정보부터 버릴 것입니다.

Anomaly Detection with Variational Autoencoders

이처럼 VIB는 훌륭한 regularizer로 오버피팅을 막아주며, 결과적으로 이것은 마치 주어진 상황에서 최적의 병목 구간 크기를 갖게 하는 효과를 갖습니다. VIB를 통해 VAE는 vanilla 오토인코더에 비해 훨씬 나은 성능의 이상탐지(anomaly detection) 성능을 제공합니다. 실험을 통해 우리는 기존의 AE는 너무 큰 bottleneck을 가지면 identity function이 되며 이상탐지 성능이 떨어지는 것에 반해, VAE는 bottleneck의 크기가 커질수록 이상탐지 성능이 오르는 효과를 갖는 것을 확인할 수 있었습니다. 따라서 AE 기반의 anomaly detection을 수행할 때, 기존에는 bottleneck의 크기를 hyper-parameter로 튜닝해야 했던 반면에, VAE의 경우에는 튜닝을 할 필요가 거의 없어졌습니다.

Anomaly Detection with Adversarial Autoencoders

Adversarial Autoencoders(AAE) [9]는 VAE 만큼 널리 쓰이는 오토인코더 중에 하나이며, 마찬가지로 anomaly detection에서도 널리 활용되고 있습니다. [10] VAE는 최적화 과정에서 KLD term을 작게 만들기 위해 latent distribution을 gaussian의 형태에 가까워지지만, 실제 gaussian 분포를 따르지는 않습니다. 하지만 AAE는 latent distribution을 검사하는 discriminator를 도입하여, 원하는 형태의 latent distribution을 강제시킬 수 있습니다. 이러한 특성은 unimodal normality 가정과 함께 쓰이면 $P(z)$ 를 구하는데 용이하게 사용될 수 있습니다. [10]

Summary

오토인코더는 고차원인 입력 차원에서 저차원인 병목 구간의 차원으로 맵핑 과정을 압축과 해제를 반복하며 학습합니다. 이 과정에서 information bottleneck이 만들어지게 되며, 자동으로 입력 샘플 복원을 위한 중요한 특징(feature)과 중요하지 않은 특징을 구분할 수 있는 능력을 학습합니다. — 이것은 매니폴드 가설에 의해서도 설명이 가능합니다. 하지만 정상 데이터만을 활용하여 고차원에서 저차원의 맵핑 과정을 학습하기 때문에, 잠재공간(latent space)의 정보를 활용하여 anomaly detection을 수행하는 것은 새로운 가정을 도입하는 것(unimodal normality)입니다. 따라서 보통은 잠재공간의 정보를 활용하지 않습니다. [8] 또한 VAE를 통해 anonamly detection을 수행하게 되면 VIB의 특성을 활용하여 가장 큰 hyper-parameter인 bottleneck 크기를 튜닝할 필요가 없어집니다. 추가로 $P(z)$ 를 활용하고자 할 때, AAE를 사용하게 되면 latent의 분포를 gaussian과 같은 형태로 강제할 수 있어, latent variable의 확률값을 구하는데 활용 가능합니다.

References

[1] Stanislav Pidhorskyi et al., Generative Probabilistic Novelty Detection with Adversarial Autoencoders, NeurIPS, 2018
[2] Lei et al., Geometric Understanding of Deep Learning, Arxiv, 2018
[3] Tishby et al., The information bottleneck method, Annual Allerton Conference on Communication, Control and Computing, 1999
[4] Kingma et al., Auto-Encoding Variational Bayes, ICLR, 2014
[5] Tishby, Information Theory of Deep Learning, https://youtu.be/bLqJHjXihK8
[6] Tishby et al., Deep learning and the information bottleneck principle, IEEE Information Theory Workshop (ITW), 2015
[7] Alemi et al., Deep Variational Information Bottleneck, ICLR, 2017
[8] Ki Hyun Kim et al., Rapp: Novelty Detection with Reconstruction along Projection Pathway, ICLR, 2020
[9] Makhzani et al., Adversarial autoencoders. Arxiv, 2015.
[10] Stanislav Pidhorskyi et al., Generative Probabilistic Novelty Detection with Adversarial Autoencoders, NeurIPS, 2018

Introduction to Deep Anomaly Detection

이번 포스트에서는 Anomaly Detection에 대해 소개해보고자 합니다. Anomaly detection(이상탐지) 알고리즘은 주어진 샘플에 대한 정상 여부를 판별하기 위한 알고리즘 입니다. 예를 들어 신용카드 사기 여부(credit card fraud detection)나, CCTV와 같은 비디오 감시(video surveillance), 자율 자동차 주행(autonomous driving)과 같은 다양한 분야에서 사용될 수 있으며, 특히 마키나락스가 집중하고 있는 산업(제조업)에서는 장비 이상 탐지, 불량 제품 탐지와 같은 중요한 문제를 해결할 수 있습니다. 하지만 anomaly detection의 중요성에 비해 이에 대한 연구는 아직 활발하지 않습니다.

앞으로의 포스팅에서는 딥러닝을 활용한 anomaly detection과 마키나락스가 개발한 RaPP 방법에 대해서도 다루도록 하겠습니다. 또한, 오토인코더 이외의 다양한 방법들을 활용한 anomaly detection 방법들에 대해서도 리뷰하도록 하고자 합니다.

Motivations

사실 이상 또는 비정상을 탐지하는 것은 단순한 binary classification(이진 분류)문제로 생각해 볼 수 있습니다. Binary classification에 대한 방법들은 잘 알려져 있으며, 딥러닝을 통해서도 쉽게 구현이 가능합니다. 하지만 기존의 전형적인 분류 알고리즘들은 다음과 같은 이유들로 인해서 적용될 수 없습니다. 앞으로 서술할 내용들은 [1]에서도 살펴보실 수 있습니다.

Highly imbalanced data

실제 세상에서 우리는 당연히 정상 데이터를 비정상 데이터에 비해서 훨씬 쉽게 얻을 수 있습니다. 즉, 비정상 데이터는 정상 데이터에 비해서 매우 적게 수집될 가능성이 높습니다. 이렇게 수집된 불균형한 데이터셋(imbalanced dataset)을 통해 딥러닝(머신러닝)을 수행하게 된다면, 모델은 각 샘플들에 대해 동등하게 학습하였을때 비정상 데이터에 대한 특징을 잘 배우지 못하게 될 것입니다. 또한 예를 들어 99%의 정상 데이터들로 구성되어 있다고 가정한다면, 시스템은 그냥 아무런 근거 없이도 정상이라고 찍어(guess)버리면 평균적으로 100점 만점에 99점을 받게 될 것입니다. 따라서 이와 같이 극심한 불균형 데이터셋에 대해서 판별하는 모델을 만들고자 할 때, 우리는 anomaly detection 알고리즘을 활용하게 됩니다.

Open-world classification problem

어쩌면 그럼 우리는 99%의 정상 데이터로 가득한 데이터셋을 학습할 때, 비정상을 99배 더 학습하도록 하는 방법도 생각해 볼 수 있을 것 입니다. 하지만 아쉽게도 이 방법을 통해서도 문제를 해결할 수 없습니다. 왜냐하면 대부분의 경우 비정상 데이터는 정상 데이터에 비해서 다양한 패턴을 가질 것 입니다. 하지만 불균형 데이터셋에서도 알 수 있듯이, 우리는 이러한 다양한 특징들을 배우기에는 비정상 데이터의 양이 턱없이 모자랍니다. 게다가 예를 들어 비정상 패턴들을 통해 비정상 클래스를 정의한다고 하면, 우리는 애초에 비정상 클래스가 유한하게 정의될 수 있는지도 알 수 없습니다. 이러한 문제 상태를 open-world classification 이라고 하며, 당연히 그럼 우리는 수집된 비정상 데이터를 통해 모든 비정상 데이터의 패턴을 배울 수 없습니다.

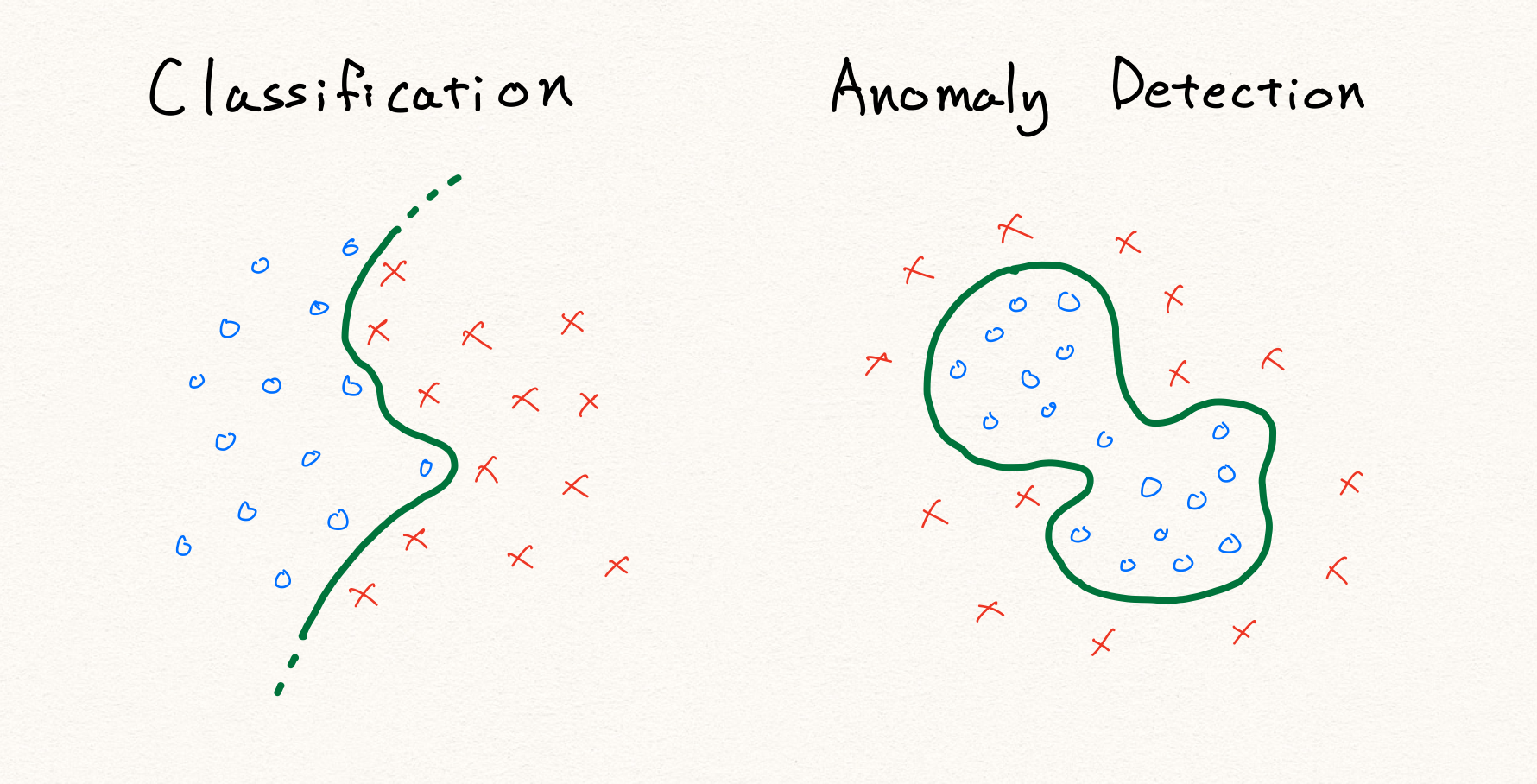
분류 문제와 이상탐지 문제의 차이

예를 들어 위의 그림과 같이 기존의 분류 문제라면 단순히 정상과 비정상을 가르는 decision boundary를 찾는 문제가 될 것 입니다. 하지만 정의에 따라 anomaly detection에서 비정상 데이터는 정상 영역 이외의 영역에 분포하는 데이터를 가리킵니다. 따라서 위와 같이 단순히 주어진 데이터를 통해 경계선을 찾게 된다면, 학습 데이터 내의 불량 데이터에 대해서만 정상적으로 판별할 수 있는 모델이 될 것 입니다. 결국 우리는 기존의 전형적인 판별 알고리즘을 사용하여 anomaly detection을 구현할 수 없습니다.

Before Deep Learning

딥러닝 이전에도 anomaly detection을 하기 위한 다양한 시도들이 있었습니다. 예를 들어 One-class SVM 또는 Gaussian Mixture Model (GMM)과 같은 알고리즘을 사용하여 정상 데이터의 영역을 정의하거나, 정상 데이터의 분포를 추정하는 방법을 통해 anomaly detection을 수행하였습니다. 특히 kernel-SVM의 경우에는 DNN(deep neural network)를 커널로 사용하여 여전히 사용되기도 합니다.

PCA

그 중에서도 우리는 PCA(주성분 분석)에 대해서 가장 주목하고자 합니다. 앞으로 설명할 오토인코더와 가장 유사한 아이디어로 동작하기 때문입니다. (아마도 PCA가 오토인코더의 특수한 형태라고 설명할 수 있을 것 같습니다.)

PCA는 데이터의 분포에 따라 그 분산을 가장 최대로 하는 축을 찾아냅니다. 우리는 보통 SVD(singular value decomposition)을 통해 PCA를 수행할 수 있습니다. 좀 더 자세한 설명은 SVD에 대한 내용을 찾아보시기 바랍니다.

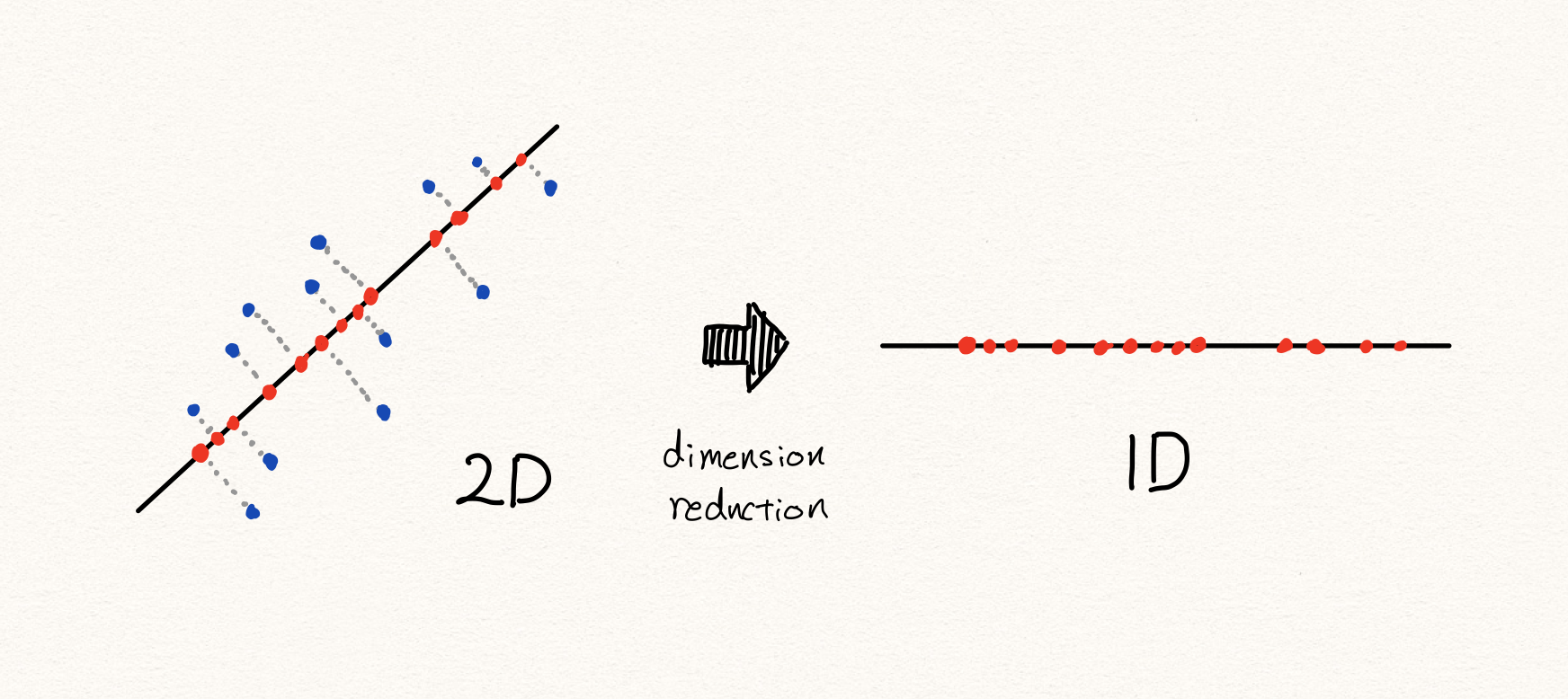
PCA가 수행된 예제

우리는 이처럼 선형적으로 차원을 축소할 수 있습니다. 이때 샘플들은 선택된 축들로 projection(투사)됩니다. 이렇게 낮은 차원의 공간들에 존재하는 샘플들을 다시 원래 높은 차원의 공간으로 복원하게 되었을 때, 차원 축소 전 원래의 샘플의 위치와 비교하여 거리가 먼 샘플은 비정상이라고 판별하게 됩니다.

PCA에서 비정상 샘플을 판별하는 예제

이를 수식으로 나타내면 다음과 같이 표현할 수 있을 겁니다.

\[\begin{gathered} f:x\rightarrow\mathbb{R}^{n}\text{, where }x\in\mathbb{R}^{m}, \\ g:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}\text{ and }\hat{x}=g\circ{f}(x)\text{, where }m>n. \\ \\ \text{anomaly\_score}(x)=||x-\hat{x}||, \\ \text{is\_anomalous}(x)=\begin{cases} 1\text{ if anomaly\_score}(x)\ge\tau, \\ 0\text{ otherwise.} \end{cases} \end{gathered}\]

우리는 PCA를 통해 고차원의 공간에서 저차원의 공간으로 맵핑하는 함수를 배울 수 있습니다. 이후에 다시 복원된 값과 원본 값을 비교하여 차이가 작을수록 정상이다라고 할 수 있습니다.

Discussion

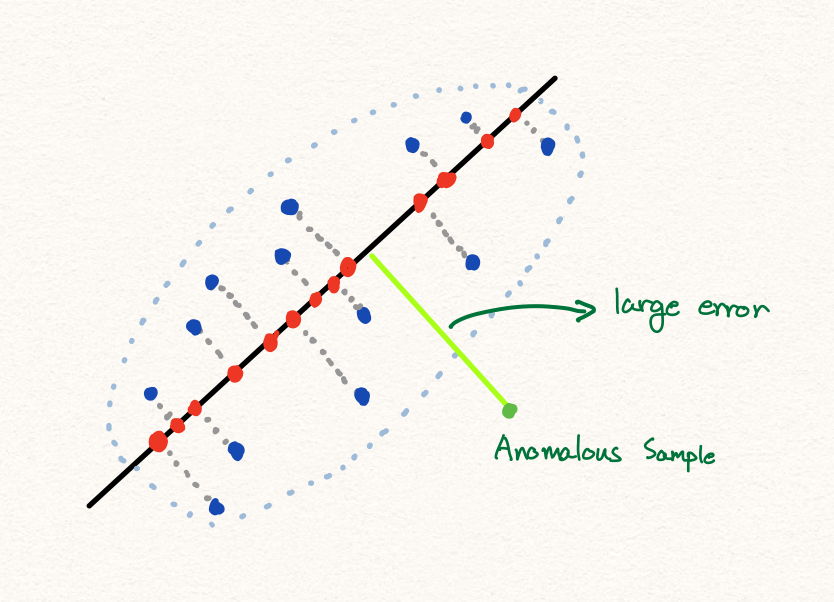
이와 같이 PCA를 통해 우리는 anomaly detection을 수행할 수 있습니다. 하지만 많은 경우에 PCA는 훌륭하게 동작하지만, 아래와 같은 경우에는 잘 동작하지 않을 수 있습니다.

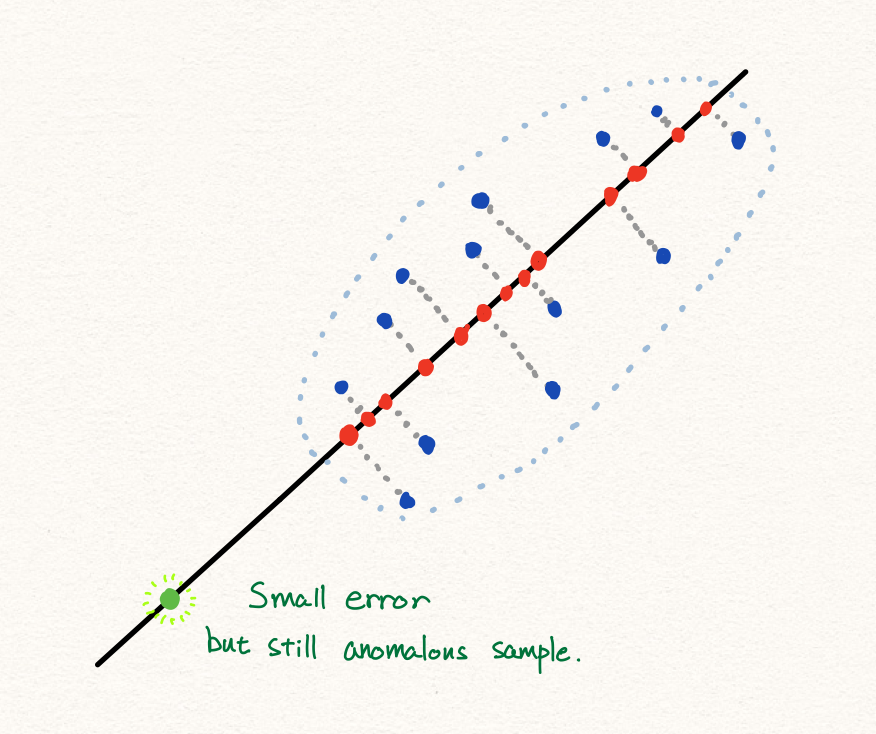
PCA에서 해결할 수 없는 이상 데이터의 예

또한 만약 데이터의 분포가 아래와 같다면, 선형적인 축소 방식으로 인해서 우리는 PCA를 통해 성공적인 anomaly detection을 수행하지 못할 것 입니다. 따라서 우리는 딥러닝을 통해 비선형적인 데이터에 대해서 anomaly detection을 수행하고자 합니다.

PCA에서 해결할 수 없는 비선형 데이터의 분포

Problem Setups in Anomaly Detection

비록 anomaly detection에 대해서 활발한 연구가 부족하지만, 문제를 정의하는 다양한 방법들이 존재합니다. 따라서 입문자들이 느끼기에는 다소 혼란스러울 수 있습니다. 이번 섹션에서는 다양한 anomaly detection에 대한 문제 정의와 실험 환경 셋팅에 대해서 이야기 하고자 합니다.

Out-of-distribution

먼저 computer vision 분야에서 활발하게 연구되고 있는 주제입니다. 예를 들어 MNIST를 대상으로 학습된 이미지 분류 네트워크가 있다고 가정해 보겠습니다. 이 네트워크는 매우 성능이 좋아서 MNIST 클래스에 대한 성공적인 예측을 잘 수행합니다. 만약 이 네트워크에 MNIST와 똑같은 크기의 사람 얼굴 사진을 넣으면 어떤 예측이 나올까요? 그 네트워크는 뭔가를 예측할 것이고, 예를 들어 얼굴이 동그란 모양이니 우연히 0에 대해서 높은 softmax 결과값으로 예측했다고 해보죠. 그럼 우리는 과연 네트워크의 그 값을 믿어야 할까요? 신경망은 학습데이터의 도메인에 대해서만 학습이 되었기 때문에, 학습데이터 영역 밖의 데이터가 주어지면 어떻게 동작할지 전혀 알 수 없습니다. 또한 이러한 경우에 출력된 값은 믿을 수 없을 것 입니다. OOD(Out-of-distribution) 문제는 이러한 문제를 해결하고자 합니다.

이를 위해서 OOD는 보통 학습한 데이터와 다른 데이터셋이 주어졌을 때, 이것을 판별해내는 것입니다. 보통 OOD 알고리즘을 평가하기 위해서는 두 개 이상의 데이터셋이 있을 때, 하나의 데이터셋만을 학습한 신경망에 학습에 참여하지 않은 데이터셋이 주어지는 형태로 실험이 진행 됩니다. 즉, MNIST를 학습한 신경망에 MNIST와 F-MNIST가 주어진다면 신경망이 이를 구분해 낼 수 있는지 여부가 중요하게 적용됩니다. (한마디로 데이터셋 분류기랄까요?) 결과적으로 우리는 이미지 분류기를 통과하기에 앞서, 주어진 입력을 OOD 모델을 통해 적합한지 따져볼 수 있을 것 입니다. – 추가로 OOD는 adversarial attack과 연관지어 연구가 이루어지기도 합니다. [3, 4]

Semi-supervised Anomaly Detection

다음은 마키나락스가 주로 다루는 주제에 대해 소개하고자 합니다. 보통 anomaly detection이라하면 이 문제에 대해서 이야기 하는 것 입니다. [6] 널리 사용되는 만큼 이외에도 outlier detection, novelty detection [5] 과 같은 다양한 이름을 갖고 있습니다.

이 문제는 아래와 같은 방법을 통해 학습과 평가가 진행됩니다. 먼저 모델을 학습할 때에는 정상 데이터만을 갖고 학습합니다. 그럼 학습이 완전히 종료된 이후에 테스트 과정에서 비정상 데이터가 주어졌을 때, 모델이 정상인지 비정상인지 판별할 수 있는지 여부가 가장 중요한 평가 요소입니다. 어쩌면 OOD와 거의 유사한 형태로 진행되는 것을 볼 수 있습니다. 다만 이 주제과 OOD의 차이점은 보통 동일한 데이터셋(또는 연관있는 데이터셋)내에서 이루어진 다는 점이며, 크게 아래와 같은 두 가지 케이스로 진행됩니다.

Unimodal normality case

먼저 우리는 정상의 패턴이 하나이고, 비정상 패턴이 다양한 형태를 상상해 볼 수 있습니다. 예를 들어 MNIST의 경우에 임의의 숫자 클래스 하나를 정상 데이터로 가정하고 학습을 진행합니다. 이후에 테스트 과정에서 10가지 클래스 모두를 포함하여 모델이 정상 클래스와 비정상 클래스를 잘 구별하는지 테스트할 수 있을 것입니다. 이 케이스는 one-class classification [7] 이라는 이름으로도 널리 알려져 있습니다.

Multimodal normality case

근데 사실은 어쩌면 정상 또한 다양한 패턴으로 나타날 수 있을 것 입니다. 예를 들어 우리가 자동차 엔진에 대해서 anomaly detection을 수행한다고 하였을 때, 엔진은 4가지의 다른 상태(흡기, 압축, 폭발, 배기)로 정의 될 수 있고, 각 상태는 서로 꽤 상이할 수 있습니다. 따라서 우리는 정상 데이터가 단순히 한 가지라고 가정하고 문제에 접근하는 것은 상황에 따라 옳지 않은 방법이 될 수 있습니다.

이 문제에 대한 모델을 학습하고 평가하기 위해서는 다음과 같은 과정이 필요합니다. 예를 들어 MNIST 9개의 클래스를 임의로 정상 데이터로 가정한다면, 9가지 클래스를 통해 모델 학습을 진행합니다. 학습이 종료된 이후에, 나머지 비정상으로 간주된 1개의 클래스를 합쳐 전체 10개의 클래스를 통해 정상 클래스와 비정상 클래스를 분류해내는지 평가합니다. 보통은 앞서 설명한 unimodal normality case에 비해서 어려운 setup으로 취급되고, 따라서 모델도 더 낮은 성능을 보이게 됩니다.

비록 우리는 모델을 학습할 때에는 비정상 데이터를 보여주지 않지만 정상데이터만 넣어주어야 한다는 점에서, 수집된 데이터들을 정상 데이터와 비정상 데이터로 레이블링 해야 하며 이와 같은 이유 때문에 semi-supervised learning 방식에 속하는 것이라고 볼 수 있습니다.

우리 마키나락스는 주로 이 방법에 대해서 연구를 수행하며, novelty detection이라는 이름으로 부르고 있습니다. 그 이름에서 볼 수 있듯이, 데이터의 참신성(novelty)을 탐지하기 위한 방법임을 알 수 있습니다. 좀 더 자세한 셋업은 ICLR 2020에 출판된 마키나락스의 페이퍼 RaPP[5] 를 참고하세요.

Unsupervised Anomaly Detection

그럼 우리는 수집된 데이터들이 정상 또는 비정상 레이블링이 전혀 없는 경우에 대해서도 생각해 볼 수 있을 것입니다. [8] 수집된 데이터를 일괄적으로 학습용과 평가용으로 나눈 후에 모델 학습과 평가를 진행할 수 있겠지요. 이와 같은 방법을 unsupervised anomaly detection이라고 부릅니다. 이 경우에도 마찬가지로 unimodal normality case와 multimodal normality case로 나눠볼 수 있을 것입니다.

아쉽게도 anomaly detection에 대한 집중적인 연구가 이루어지지 않은 덕분에 위의 문제 정의들에 대한 약간의 차이가 있을 수 있습니다. 예를 들어 semi-supervised anomaly detection 또는 novelty detection을 unsupervised anomaly detection으로 부르기도 합니다. 따라서 논문을 접할 때 문제 setup에 대해서 유의하며 읽어야 합니다.

Evaluations

기존의 분류 알고리즘을 사용할때는 보통 해당 클래스에 속할 확률(또는 likelihood)값을 얻게 되어, 각 클래스별 확률값 비교를 통해 가장 높은 확률을 갖는 클래스를 선택하게 됩니다. 하지만 anomaly detection의 경우에는 (supervised learning에 기반하지 않기 때문에) 클래스별 확률값이 아닌, 샘플 자체에 대한 anomaly score가 주어지는 경우가 많습니다. 따라서 anomaly score에 대한 threshold 설정이 필요합니다.

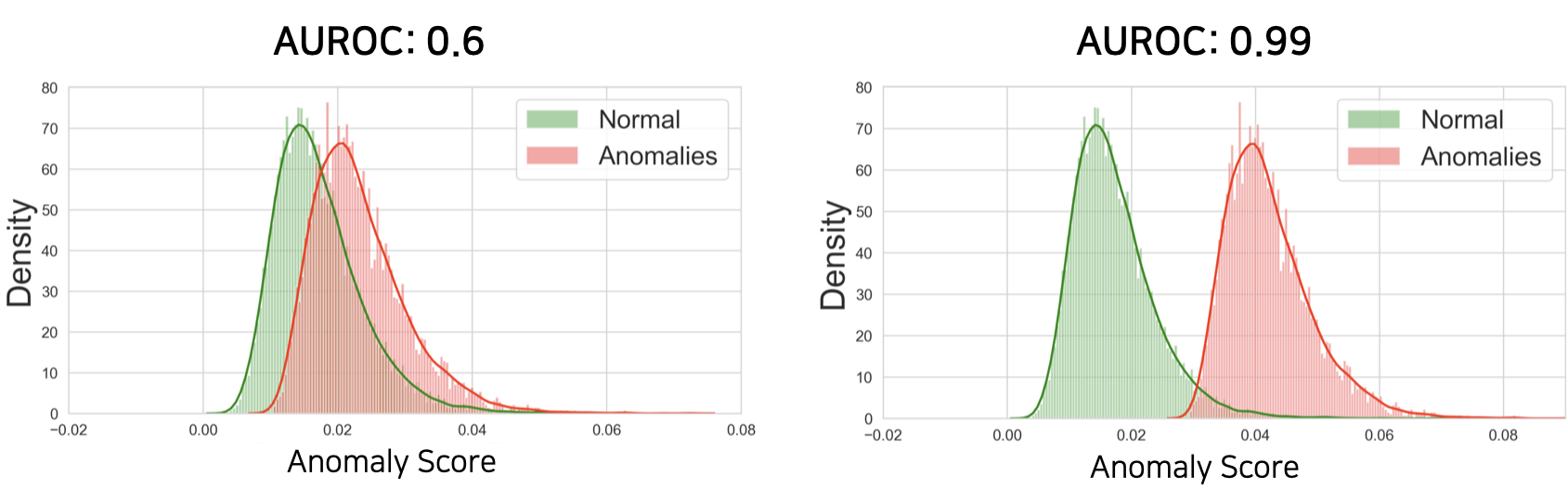
정상 데이터의 anomaly score 분포와 비정상 데이터의 anomaly score 분포

예를 들어 우리는 테스트 데이터셋에 대해서 위와 같이 anomaly score들을 구하여 anomaly score의 분포로 만들어 볼 수 있습니다. 이때 두 분포가 충분히 겹쳐있지 않다면, 두 분포 사이를 잘 가로지르는 threshold를 설정할 수 있습니다. 하지만 물론 우리는 테스트셋을 실제로는 볼 수 없기 때문에 이와 같이 threshold를 구하는 것은 어렵고, 보통은 학습 데이터의 정상 데이터의 분산의 크기를 보고 결정하기도 합니다.

어쨌든 우리는 정상 데이터의 anomaly score 분포와 비정상 데이터의 anomaly score 분포가 겹쳐있는 부분이 적을수록 threshold를 정하는 작업이 굉장히 수월해질것 입니다. 왜냐하면 만약 두 분포가 정말 멀리 떨어져있다면, 적당히 대충 threshold를 정해도 두 분포를 잘 갈라낼 것이기 때문입니다. — robust한 알고리즘이라고 할 수 있습니다. 따라서 보통 우리는 두 분포의 분리의 정도를 측정하는 방법인 AUROC를 통해 anomaly detection 성능을 측정합니다. (가끔 AUPR을 통해서도 anomaly detection 성능을 측정합니다.)

앞서 언급한대로 PCA의 경우에는 reconstruction error(원본값과 복원값의 차이의 크기)를 anomaly score로 삼아 점수가 큰 경우에 비정상으로 간주합니다. 즉, 복원이 잘 되지 않는 샘플일수록 비정상으로 간주합니다.

Deep Anomaly Detections

예전부터 위와 같은 문제 정의들을 통해서 연구가 이루어져왔고, 당연히 딥러닝의 눈부신 성과에 힘입어 딥러닝을 통해 anomaly detection을 해결하고자 하는 시도들이 이어지고 있습니다. 우리는 크게 4가지 알고리즘으로 나눠 볼 수 있습니다.

Deep-kernel-based Anomaly Detections

Kernel-SVM과 같이 기존의 커널 기반 머신러닝 알고리즘에 Deep Neural Networks (DNN)을 활용한 커널을 사용하는 방식입니다. 이 포스트에서는 자세히 다루지 않도록 합니다.

Auto-encoder based Anomaly Detections

오토인코더는 PCA처럼 차원축소를 통해 피쳐를 추출해내지만, 그것을 비선형적으로 수행한다는 점에서 큰 차이가 있습니다. (오토인코더의 non-linear activation function을 없애고 학습하면 PCA와 비슷하게 동작합니다.) 오토인코더는 쉽게 말해 압축과 해제를 하며 피쳐를 추출합니다. 예를 들면, MP3의 경우에는 일반적인 사람이 듣기에는 실제 음원과 큰 차이가 없지만, 용량에서는 큰 차이를 보입니다. 이는 사람이 잘 듣지 못하는 주파수 영역의 데이터는 날려버리고, 실제로 중요한 주파수 영역만 압축했기 때문입니다. — 손실 압축을 수행합니다. 마찬가지로 오토인코더도 주어진 고차원 공간상의 샘플을 bottle-neck(병목) 구간의 저차원 공간으로 맵핑하는 방법을 학습하는 과정에서 (이를 다시 고차원 공간으로 복원해야 하기 때문에) 복원에 필요없는 정보부터 버리게 될 것 입니다.

이처럼 오토인코더는 인코딩(encoding)과 디코딩(decoding) 과정을 통해서 스스로 특징(feature)을 추출하는 방법을 배웁니다. 하지만 MNIST에 대한 복원 결과를 보면 알 수 있듯이, 보통은 blur 하게 복원되는 특징이 있습니다. 이는 MSE 손실 함수를 사용했기 때문이라고 볼 수 있습니다. MSE 손실 함수는 불확실한 부분에 대해서는 평균값으로 예측하도록 동작하기 때문입니다. 추가로 우리는 단순한 오토인코더 뿐만 아니라 다양한 오토인코더(e.g. VAE, AAE) 등을 활용하여 anomaly detection을 구할 수 있습니다. — 데이터셋에 따라 VAE와 AAE가 더 뛰어난 성능을 보이기도 합니다. [2, 5, 6]

따라서 PCA와 같이 복원된 샘플에 대해서 원본 샘플과의 차이를 비교하는 방식인 reconstruction error based anomaly detection 에서는 성능이 떨어질 우려가 있습니다.

Generative Adversarial Network based Anomaly Detections

복원 오차에 기반한 anomaly detection 방식에서 MSE 손실함수의 사용으로 인한 복원 성능 하락은 anomaly detection 성능에 영향을 끼칠 수 있습니다. 따라서 오토인코더 기반 방식의 단점을 보완하기 위해 제안된 방법은 GAN을 활용하여 anomaly detection을 수행하는 것입니다. [9, 10, 11] 하지만 GAN의 경우에는 generator와 discriminator 사이의 적대적 학습을 통해 모델이 학습되기 때문에, 오토인코더와 달리 직접적으로 차원 축소를 수행하는 모듈이 존재하지 않습니다. 이는 GAN이 사실은 주로 생성 자체를 위한 모델이고, 차원 축소를 위한 모델은 아니기 때문입니다. 하지만 anomaly detection은 테스트 과정에서 샘플이 주어지면 이를 차원 축소 이후에 복원하는 과정을 거쳐야 하기 때문에, 차원 축소를 위한 모듈이 필요합니다.

따라서 기존의 GAN 기반의 anomaly detection 방법들은 이를 해결하기 위한 여러가지 방법들을 제시하였습니다. 예를 들어 AnoGAN [9]의 경우에는 이를 해결하기 위해서 generator로부터 생성된 $\hat{x}$ 과 $x$ 와의 차이를 최소화하는 latent variable $z$ 를 찾도록 back-propagation을 수행하는 방법을 수행합니다. — 추후 GAN에 대한 anomaly detection 포스트를 다루도록 하겠습니다.

아쉽게도 MSE의 단점을 보완하고자 제안된 GAN의 경우에는 CNN에서만 동작할뿐더러, generator와 discriminator의 균형있는 학습도 굉장히 큰 장애물로 작용합니다. 또한 reconstruction error가 낮다고 무조건 모델의 성능이 좋은 것도 아님을 실험적으로 알 수 있었으므로, 마키나락스는 주로 오토인코더에 기반한 anomaly detection을 수행합니다.

Self-supervised Learning based Anomaly Detections

가장 최근에 제안된 방법으로, 학계에서 주목받고 있는 self-supervised learning 기법을 활용하여 anomaly detection에 적용하였습니다. 물론 오토인코더도 주어진 입력을 똑같이 복원하도록 학습한다는 점에서, self-supervised learning에 속할 수 있습니다. 하지만 여기서 소개하고자 하는 방법들은 좀 더 다양한 objective를 수행하도록 학습시킨다는 점에서 다릅니다.

예를 들어 2018년 NIPS에서 제안된 논문인 Deep Anomaly Detection Using Geometric Transformations [12] 에서는 주어진 이미지에 대해서 미리 정의한 변형(transformation)을 준 이후에, 네트워크가 변형의 종류를 맞추도록 학습시킵니다. 그럼 테스트 과정에서 비정상 샘플에 변형이 추가되었을 때, 네트워크는 어떤 변형이 추가되었는지 잘 맞추지 못할 것입니다. 이 논문은 비록 변형 방법이 이미지에 국한되지만, 새로운 방법을 제시한 논문으로 주목 받았습니다.

Summary

이번 포스트에서는 anomaly detection에 대해 소개하고, 다양한 문제 정의와 이를 해결하기 위한 딥러닝 알고리즘들을 소개하였습니다. 추후 이어질 포스팅에서는 각각의 알고리즘에 대해서 좀 더 자세히 소개하고자 합니다.

References

[1] Ki Hyun Kim, Operational AI: Building a Lifelong Learning Anomaly Detection System, DEVIEW, 2019
[2] Jinwon An et al., Variational Autoencoder based Anomaly Detection using Reconstruction Probability, SNU Data Mining Center, 2015
[3] Anh Nguyen et al., Deep Neural Networks are Easily Fooled: High Confidence Predictions for Unrecognizable Images, CVPR, 2015
[4] Ian J. Goodfellow et al., Explaining and Harnessing Adversarial Examples, Arxiv, 2014
[5] Ki Hyun Kim et al., RaPP: Novelty Detection with Reconstruction along Projection Pathway, ICLR, 2020
[6] Stanislav Pidhorskyi et al., Generative Probabilistic Novelty Detection with Adversarial Autoencoders, NeurIPS, 2018
[7] Lukas Ruff et al., Deep One-Class Classification, ICML, 2018
[8] Siqi Wang et al., Effective End-to-end Unsupervised Outlier Detection via Inlier Priority of Discriminative Network, NeurIPS, 2019
[9] Thomas Schlegl et al., Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery, Arxiv, 2017
[10] Houssam Zenati et al., Efficient GAN-Based Anomaly Detection, Arxiv, 2018
[11] Ilyass Haloui et al., Anomaly detection with Wasserstein GAN, 2018
[12] Izhak Golan et al., Deep Anomaly Detection Using Geometric Transformations, NeurIPS, 2018

Generative Adversarial Networks (GAN)

\[\underset{G}{argmin}\text{ }\underset{D}{argmax}\mathcal{L}(G, D)=\mathbb{E}_{Z\sim P(Z)}[\log{D(Z)}] + \mathbb{E}_{X\sim P(X)}{[\log{(1-D(G(X)))}]}\]

Variational Auto-Encoder (VAE)

Minimize loss.

\[\mathcal{L}(\phi, \theta)=-\mathbb{E}_{X\sim P(X)}[\mathbb{E}_{Z\sim q_\phi(Z|X)}[\log{p_\theta(X|Z)}] - KL(q_\phi(Z|X)||p(Z))]\]

Adversarial Auto-Encoder (AAE)

Minimize both losses.

\[\begin{aligned} \mathcal{L}_G&=-\mathbb{E}_{X\sim P(X)}[\mathbb{E}_{Z\sim q_\phi(Z|X)}[\log{p_\theta(X|Z) - D_\psi(Z)}]] \\ \mathcal{L}_D&=-\mathbb{E}_{X\sim P(X)}[\mathbb{E}_{Z\sim q_\phi(Z|X)}[D_\psi(Z)] + \mathbb{E}_{Z\sim P(Z)}[\log{(1-D_\psi(Z))}]] \end{aligned}\]

Adversarial Variational Bayes (AVB)

Minimize both losses.

\[\begin{aligned} \mathcal{L}_G&=-\mathbb{E}_{X\sim P(X)}[\mathbb{E}_{Z\sim q_\phi(Z|X)}[\log{p_\theta(X|Z) - D_\psi(X, Z)}]] \\ \mathcal{L}_D&=-\mathbb{E}_{X\sim P(X)}[\mathbb{E}_{Z\sim q_\phi(Z|X)}[D_\psi(X,Z)] + \mathbb{E}_{Z\sim P(Z)}[\log{(1-D_\psi(X,Z))}]] \end{aligned}\]