Back-Translation Review

 
  • Sep 30, 2020

Back-Translation Review

이번 포스팅은 Neural Machine Translation (NMT)에서 널리 사랑받고 있는 Back-Translation[1] (이하 BT)에 대해서 좀 더 이해해보는 시간을 가지려 합니다. 기존에 제안된 BT에 대해서 살펴보고, 기본 BT의 한계를 극복하기 위해 제안된 여러가지 방법들을 여러가지 관점(실험 + 수식)에서 이해해보고자 합니다.

Leverage with Monolingual Corpus

NMT는 2014년 Sequence-to-Sequence의 발명 이후로 자연어생성(NLG) 분야와 함께 큰 발전을 이루어왔습니다. 특히 제가 보았을 때, 2017년 Transformer의 발명 덕분인지, 2018년에 거의 연구의 정점을 찍은 것으로 보입니다. 즉, 구성 요소들이 잘 갖춰진 문장(e.g. 뉴스기사)들에 대해서는 이미 사람의 수준을 넘어섰다고 할 정도의 성능에 이르렀습니다.

하지만 NMT 개발을 위해서는 두 쌍의 언어가 문장 수준에서 mapping되어 있는 parallel corpus가 필수적으로 필요하고, 이는 여전히 low-resource 상황에서의 NMT에서 큰 장벽이 되고 있습니다. 예를 들어, 한국어-영어 번역은 매우 잘 연구/개발되어 있지만, 한국어-태국어와 같은 번역은 이에 반해 훨씬 미비한 상황입니다. 더욱이 인터넷 등에서 무한대로 모을 수 있는 unlabled corpus에 반해, parallel corpus는 매우 수집이 어렵고 비싸기 때문에, 한국어-영어 번역에서도 여전히 parallel corpus 수집에 대한 목마름은 항상 남아있습니다.

따라서 예전부터 단방향 코퍼스(monolingual corpus)를 활용하여 번역기의 성능을 높이고자 하는 시도들은 매우 많았고, 개인적으로도 굉장히 좋아하는 주제라고 생각합니다. – 기계번역의 꽃이랄까요. Language Model Ensemble[2]에서부터 Dual Learning[3, 4]에 이르기까지 정말 많은 연구들이 있었고, 모두 parallel corpus만을 활용한 것보다 더 나은 성능을 제공할 수 있었습니다. 하지만 BT는 굉장히 이른 시기에 제안되었음에도 불구하고, 간단한 방법으로 비교적 훌륭한 결과물을 제공하기 때문에 위의 여러가지 방법들 중에서도 가장 사랑받는 방법 중에 하나였습니다. 이 포스팅에서는 Back-Translation에 대해서 살펴보고, 여러가지 관점에서 살펴보고자 합니다.

Back-Translation

Back-Translation은 에딘버러 대학의 리코 센리치 교수가 제안한 방법으로, 센리치 교수님은 BPE를 통한 subword segmentation을 제안[5]한 분으로도 유명합니다. Parallel corpus의 부족으로 인해 겪는 가장 기본적인 문제중에 하나는, 디코더인 타깃 언어의 언어모델(Language Model, LM)의 성능 저하를 생각해볼 수 있습니다. 즉, 다량의 monlingual corpus를 수집하여 풍부한 표현을 학습할 수 있는 언어모델에 비해, parallel corpus만을 활용한 경우에는 훨씬 빈약한 표현만을 배울 수 밖에 없습니다. 따라서, 소스 언어 문장으로부터 타깃 언어 문장으로 가는 translation model(TM)의 성능 자체도 문제가 될테지만, 번역에 필요한 정보를 바탕으로 완성된 문장을 만들어내는 능력도 부족할 것 입니다.

이때, TM의 성능 저하는 parallel corpus의 부족과 직접적으로 연관이 있지만, LM의 성능 저하는 monolingual corpus를 통해 개선을 꾀해볼 수 있을 것 같습니다. 하지만 예전 Statistical Machine Translation (SMT)의 경우에는 보통 TM과 LM이 명시적으로 따로 존재하였기 때문에 monolingual corpus를 통한 LM의 성능 개선을 쉽게 시도할 수 있었지만, NMT에선 end-to-end 모델로 이루어져 있으므로 LM이 명시적으로 분리되어 있지 않아 어려움이 있습니다. BT는 이러한 상황에서 디코더의 언어모델의 성능을 올리기 위한 (+ 추가적으로 TM의 성능 개선도 약간 기대할 수 있는) 방법을 제안합니다.

보통 번역기를 개발할 경우, 한 쌍의 번역 모델이 자연스럽게 나오게 됩니다. 왜냐하면 우리는 parallel corpus를 통해 번역기를 개발하므로, 두 방향의 번역기를 학습할 수 있기 때문입니다. 이때 Back-Translation이라는 이름에서 볼 수 있듯이, BT는 반대쪽 모델을 타깃 모델을 개선하는데 활용합니다.

예를 들어 아래와 같이 parallel corpus $\mathcal{B}$ 와 monolingual corpus $\mathcal{M}$ 을 수집한 상황을 생각해볼 수 있습니다.

\[\begin{gathered} \mathcal{B}=\{(x_n, y_n)\}_{n=1}^N \\ \mathcal{M}=\{y_s\}_{s=1}^S \end{gathered}\]

그럼 자연스럽게 우리는 일단은 $\mathcal{B}$ 를 활용하여 두 개의 모델을 얻을 수 있습니다.

\[\begin{aligned} \hat{\theta}_{x\rightarrow{y}}&=\underset{\theta\in\Theta}{\text{argmax}}\sum_{n=1}^N{\log{P(y_n|x_n;\theta_{x\rightarrow{y}})}} \\ &=\underset{\theta\in\Theta}{\text{argmin}}\sum_{n=1}^N{\ell\big(f(x_n;\theta_{x\rightarrow{y}}),y_n\big)} \\ \hat{\theta}_{y\rightarrow{x}}&=\underset{\theta\in\Theta}{\text{argmax}}\sum_{n=1}^N{\log{P(x_n|y_n;\theta_{y\rightarrow{x}})}} \\ &=\underset{\theta\in\Theta}{\text{argmin}}\sum_{n=1}^N{\ell\big(f(y_n;\theta_{y\rightarrow{x}}),x_n\big)} \\ \end{aligned}\]

이때, 우리는 $\hat{\theta}_{y\rightarrow{x}}$ 를 통해서 $\mathcal{M}$ 데이터셋에 대한 추론 결과를 얻어, pseudo(or synthetic) corpus를 만들 수 있습니다. 즉, 반대쪽 모델에 monolingual corpus를 집어넣어 $\hat{x}$ 을 구할 수 있습니다.

\[\begin{gathered} \tilde{\mathcal{M}}=\{(\hat{x}_s,y_s)\}_{s=1}^S, \\ \text{where }\hat{x}_s=\underset{x\in\mathcal{X}}{\text{argmax}}\log{P(x|y_s;\theta_{y\rightarrow{x}})}. \end{gathered}\]

이제 그럼 우리는 새롭게 얻은 $\mathcal{M}$ 을 포함하여 $\mathcal{B}$ 와 함께 다시 $\theta_{x\rightarrow}$ 를 학습하면 더 나은 성능의 파라미터를 얻을 수 있다는 것이 BT입니다. 당연히 이것은 반대쪽 모델에도 똑같이 적용 가능할 것 입니다.

\[\hat{\theta}_{x\rightarrow{y}}=\underset{\theta\in\Theta}{\text{argmax}}\bigg( \sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }+\sum_{s=1}^S{ \log{P(y_s|\hat{x}_s;\theta_{x\rightarrow{y}})} } \bigg)\]

이 방법의 핵심은 pseudo sentence가 인코더에 들어가고, 실제 문장이 디코더에 들어가는 것입니다. 이에따라 인코더는 비록 큰 도움을 못받더라도, 디코더는 어쨌든 주어진 인코더의 결과값에 대해서 풍부한 언어모델 디코딩 능력을 학습할 것으로 예상할 수 있습니다.

실험 결과 및 한계

아래와 같이 BT는 굉장히 간단한 구현 방법에 비해 준수한 성능 개선 효과를 보여줍니다.

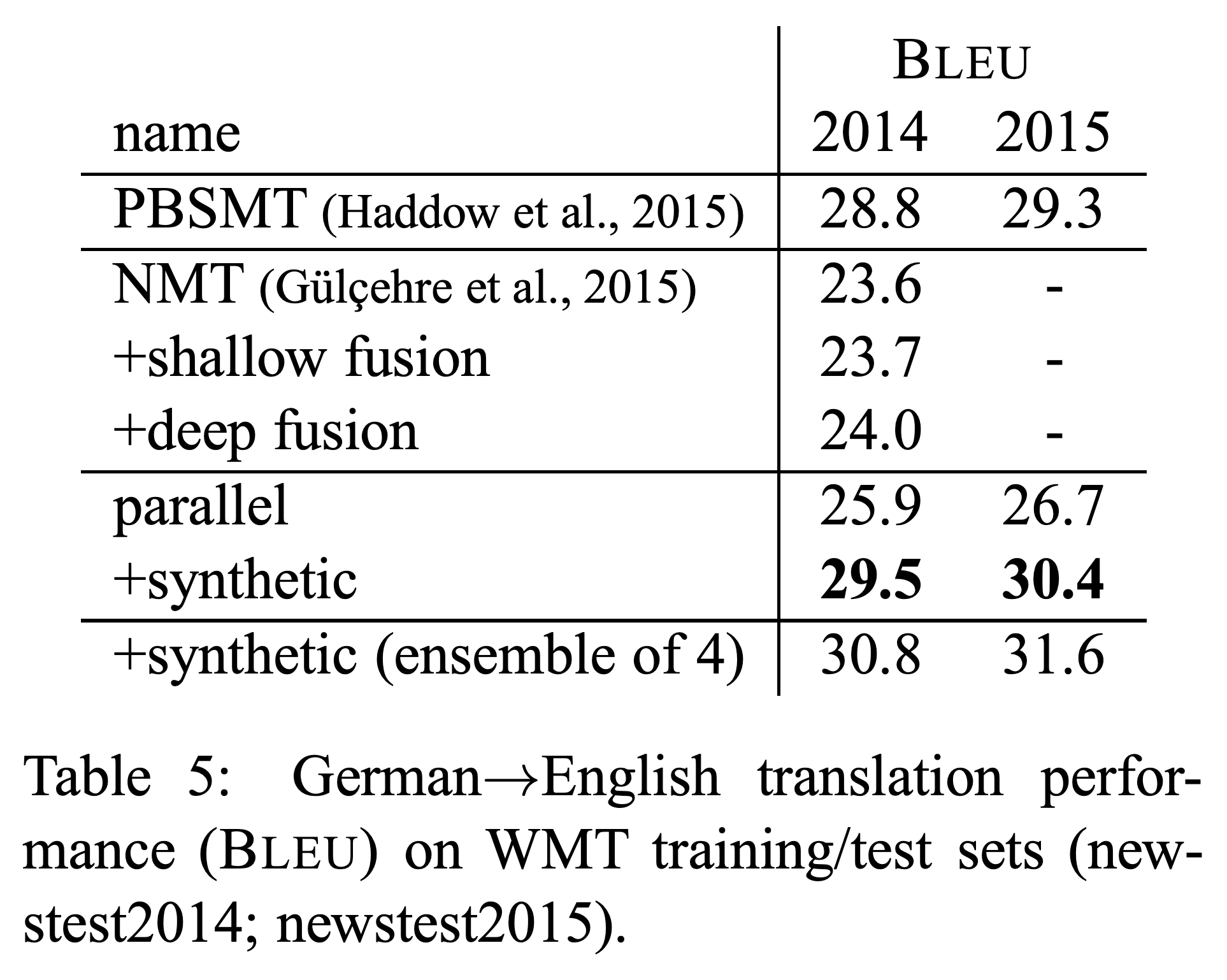
결과 테이블

그런데 중요한 점은 pseudo corpus의 양이 너무 많아서는 안된다는 것입니다. 비록 우리는 무한대에 가까운 monolingual corpus를 얻어 pseudo corpus를 만들어낼 수 있겠지만, 만약 그럴경우 pseudo corpus가 기존 parallel corpus를 압도해버릴 수 있습니다. Pseudo corpus의 경우에는 인코더에 들어갈 $\hat{x}$ 이 실제 정답과는 일부 다를 수 있기 때문이고, 더욱이 $\theta_{y\rightarrow{x}}$ 에 의해 bias가 생겨있는 상태일 것이므로, 너무 많은 양의 pseudo corpus를 활용할 경우 $\theta_{x\rightarrow{y}}$ 가 잘못된 bias를 학습할 경우도 생각해볼 수 있습니다. [6] 따라서 우리는 제한된 양의 $\mathcal{M}$ 만 활용할 수 있으며, 이는 또 하나의 하이퍼파라미터를 추가시킵니다. 그리고 이 하이퍼파라미터는 보통 기존 parallel corpus의 2~3배 정도가 적당하다고 알려져 있습니다.

Noise 추가를 통한 Back-Translation 개선

실제 모든 $\mathcal{M}$ 을 활용하지 못하고 제한된 양을 활용할 수 밖에 없기 때문에, 이 제한된 양을 좀 더 늘릴수 없을지 또 다른 연구들이 이어졌습니다. [7]에서는 pseudo corpus를 생성할 때, noise를 섞으면 BT의 성능이 더 향상되는 것을 확인하였습니다. 예를 들어 generation을 하는 과정에서 argmax(or greedy)를 통해 번역 문장을 생성하는 것보다, random sampling을 통해 random noise를 섞어주거나 beam seach 과정에서 약간의 noise를 섞어주는 것이 기존 BT보다 더 나은 성능을 제공한다는 것입니다.

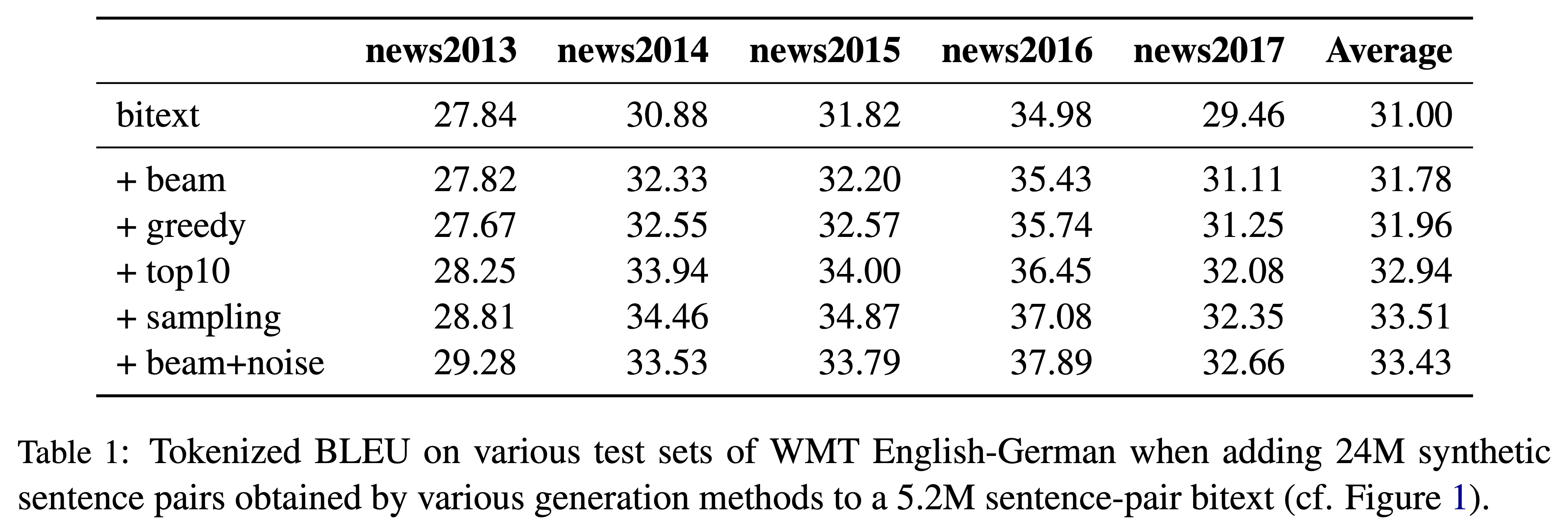
결과 테이블

이는 인코더에서 $\hat{x}$ 를 학습할 때, 기존 $\theta_{y\rightarrow{x}}$ 의 bias를 학습하는 것을 방해하는 일종의 regularization 역할로도 생각해볼 수 있습니다.

Tagged Back-Translation

여기서 한 발 더 나아가 더 쉬운 방법을 통해 더 높은 성능을 제공하는 방법도 제안되었습니다. [6]에서는 인코더에서의 잘못된 bias 학습으로 인해 번역기 전체 성능이 하락되는 것을 막기 위해, pseudo corpus에 tag를 붙인 상태로 학습하는 것을 제안하였습니다. 좀 더 정확히 말하면 인코더에 입력으로 들어가는 소스 언어의 pseudo sentence의 맨 앞에 pseudo corpus라는 tag를 넣어주어, 네트워크가 pseudo corpus에 대해서는 다르게 행동하여, 실제 테스트 환경에서는 잘못 학습된 bias로 인해 번역 성능이 낮아지는 것을 막고자 하였습니다.

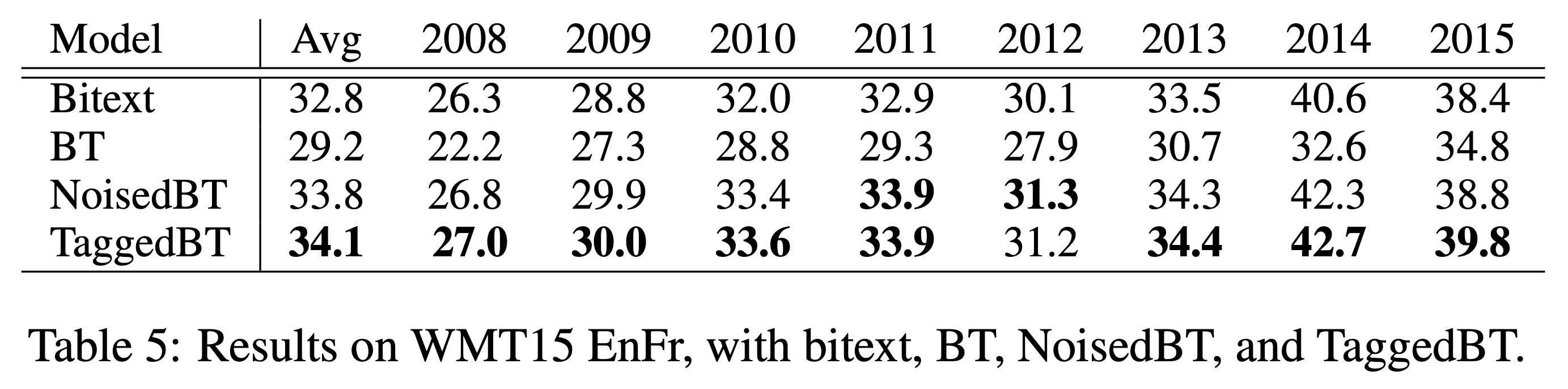
결과 테이블

이 결과 기존 BT 뿐만 아니라, Noise added BT에 비해서도 더 높은 성능 향상을 이끌어냈으며, 심지어 기존 방법에 비해 더 많은 monolingual corpus를 활용 하였을 때도 성능의 저하가 이루어지지 않는 것을 확인하였습니다. 이것은 전체 monolingual corpus를 활용할 수 없어 아쉬움이 남던 BT의 단점을 획기적으로 개선한 것이라고 볼 수 있을 것입니다.

위에서 언급하였듯이, 우리는 tag를 pseudo sentence의 맨 앞에 달아 인코더에 넣어줌으로써, 아마도 인코더는 pseudo corpus를 처리하기 위한 별도의 mode에 들어갈 것이고, 이는 잘못된 bias를 학습하는 것을 방지하여 기존의 parallel corpus 학습에 지장을 주지 않도록 하지 않을까 예상해볼 수 있습니다.

실제 Back-Translation은 효과가 있을까?

이처럼 BT를 활용한 방법들은 간단하면서도 높은 성능을 제공하는 효율성으로 널리 사랑받고 있습니다. 이때, [8]에서는 실제로 BT가 겉으로 보이는 성능 만큼이나 실제로도 번역기의 성능을 개선하는데 도움이 되는지 분석해 보았습니다. 이를 위해 이 논문에서는 아래의 3가지 질문에 대해서 BT에 실제로 어떻게 동작하는지 좀 더 검증해보고자 하였습니다. – 원문 발췌

  • Q1. Do NMT systems trained on large backtranslated data capture some of the characteristics of human-produced translations, i.e., translationese?
  • Q2. Does a tag for back-translations really help differentiate translationese from original texts?
  • Q3. Are NMT systems trained on back-translation for low-resource conditions as sensitive to translationese as in high-resource conditions?

저자는 기존의 논문들에서 사용한 테스트셋(e.g. WMT)의 입력들이 자연스러운 원문장이라기보단 상대적으로 어색한 원문장에 대한 번역문(translationese)들을 포함하고 있으며, BT 방법들이 이러한 테스트셋에서 좋은 성능을 거둘 수 있었던 것은 실제 번역성능이 올랐다기보단 translationese들을 잘 번역했기 때문이라고 주장했습니다. Pseudo sentence $\hat{x}$ 를 인코더에 넣어 학습시키는 것은 bias가 포함되어 있기 때문에, translationese를 잘 번역하도록 할 뿐 실제 원문(본문에서는 original text라고 표현)에 대한 번역 성능은 검증이 필요하다는 것입니다. 이를 위해서 저자는 아래와 같이 기존 각 연도별 WMT 테스트셋에서 original text와 translationese를 구분해서 BT와 Tagged BT의 성능을 각각 검증해보았습니다.

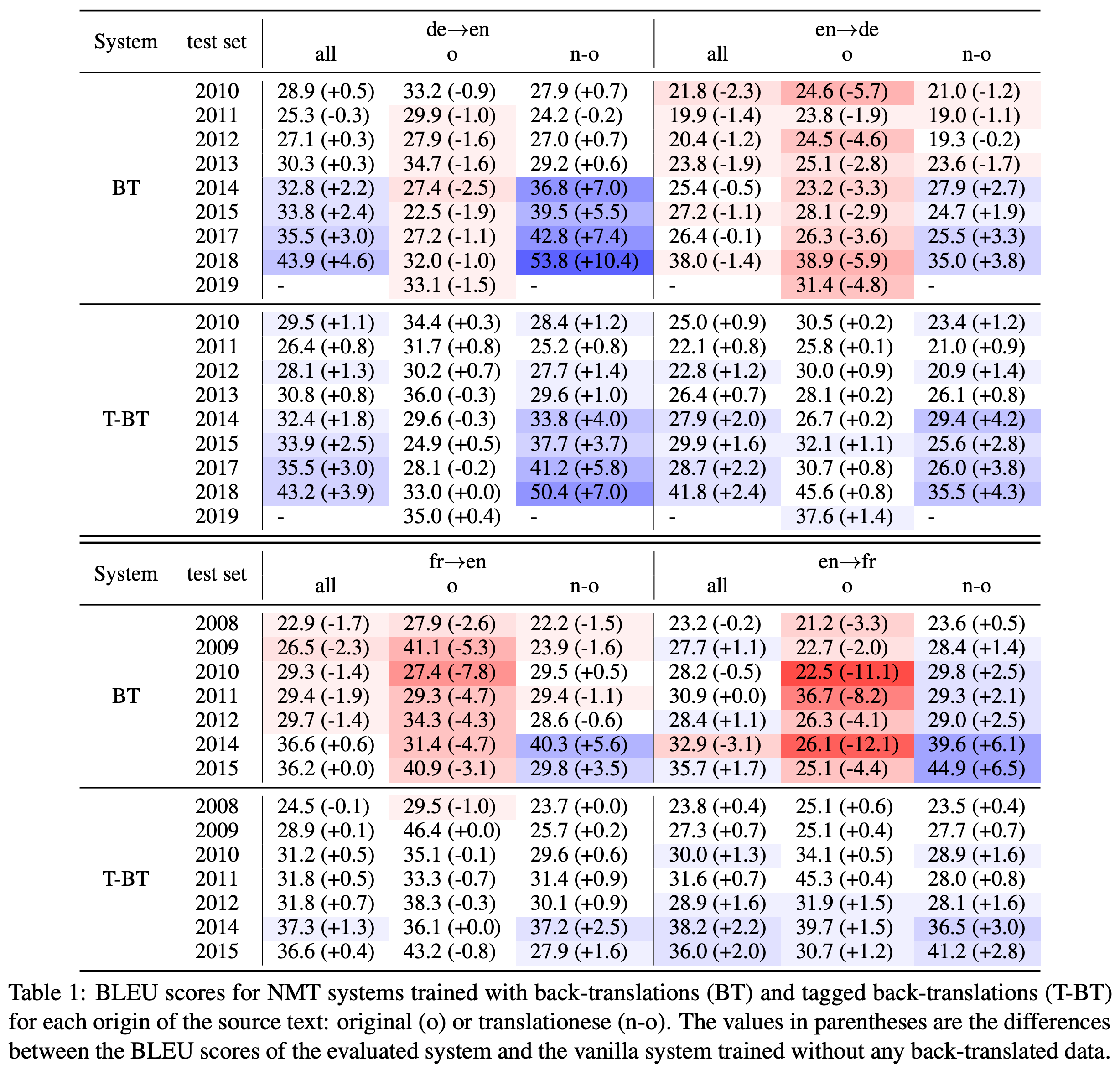
결과 테이블

그 결과 재미있게도 vanilla BT의 경우에는 translationese가 입력으로 주어졌을 때의 성능 향상만 있었을 뿐, original text에 대해서는 오히려 성능이 하락하는 것을 알 수 있습니다. 특히 translationese에 대한 성능 개선이 두드러지는 바람에, 둘이 섞인 전체 테스트셋에서는 오히려 Tagged BT에 비해 성능 향상이 더 큰 것처럼 착시 현상을 일으키기까지 합니다. 이에 반해 Tagged BT의 경우에는 translationese 뿐만 아니라, original text에서도 미미하지만 성능 개선이 있었음을 확인할 수 있습니다.

결국 BT로 인한 성능 향상의 대부분은 번역문과 같은 translationese를 입력으로 받았을 때 일어난 것으로 해석할 수 있습니다. 이것은 물론 실망스러운 결과일 수 있지만, 그렇다고 해서 실제 deploy환경에서 translationese와 같은 입력들이 전혀 없을 것은 아니기 때문에, 전혀 쓸모없는 성능 개선이라고는 볼 수 없을 것입니다.

물론 아래와 같이 low-resource 환경에서의 번역일 때는 BT와 Tagged BT 모두 번역 성능 개선에 매우 큰 도움을 주는 것을 확인할 수 있습니다.

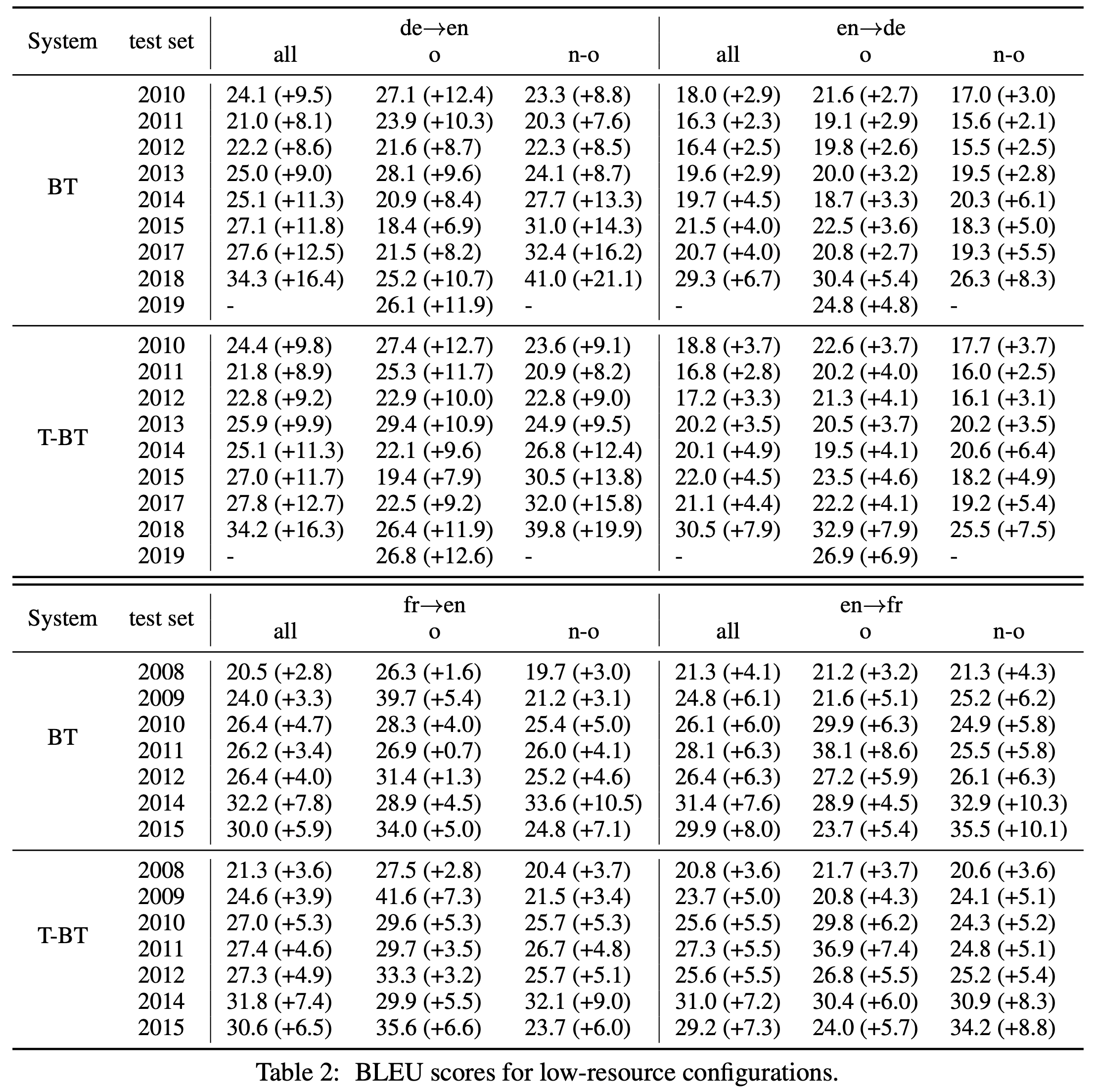
결과 테이블

여기에서도 Tagged BT가 기존 BT보다 original text에서 더 나은 성능 개선 폭을 보이는 것을 확인할 수 있습니다.

Back-Translation 수식으로 풀어보기

사실 BT는 부족한 코퍼스로 인한 디코더 언어모델의 성능개선이라는 미명아래, 직관적인 설명에 의존해서 제안되었습니다. [9]에서는 여기에 수식으로 BT를 설명하기도 하였습니다.

\[\begin{gathered} \mathcal{B}=\{(x_n, y_n)\}_{n=1}^N \\ \mathcal{M}=\{y_s\}_{s=1}^S \end{gathered}\]

아까와 같이 parallel corpus와 monolingual corpus가 수집되었다고 할 때, importance sampling을 통해 아래와 같이 수식을 전개할 수 있을 것입니다.

\[\begin{aligned} \log{P(y)}&=\log{\sum_{x\in\mathcal{X}}{ P(x,y) }} \\ &=\log{\sum_{x\in\mathcal{X}}{ P(y|x)P(x) }} \\ &=\log{\sum_{x\in\mathcal{X}}{ \frac{P(y|x)P(x)}{P(x|y)}P(y|x) }} \end{aligned}\]

그리고 Jensen’s Inequality를 활용하여 부등식을 완성할 수 있습니다. – VAE[10]의 전개와 매우 비슷합니다.

\[\begin{aligned} \log{P(y)}&=\log{\sum_{x\in\mathcal{X}}{ \frac{P(y|x)P(x)}{P(x|y)}P(y|x) }} \\ &\ge\sum_{x\in\mathcal{X}}{ P(y|x)\log{ \frac{P(y|x)P(x)}{P(x|y)} } } \\ &=\mathbb{E}_{x\sim{P(\text{x}|y)}}\big[ \log{P(y|x)} \big]-\text{KL}\big(P(\text{x}|y)\|P(\text{x})\big) \end{aligned}\]

여기서 우리가 구하고자 하는 파라미터 $\theta_{x\rightarrow{y}}$ 는 아래의 수식을 최대화 한다고 할 때, 위의 수식을 넣어 볼 수 있을 것입니다.

\[\begin{gathered} \begin{aligned} \mathcal{L}(\theta_{x\rightarrow{y}}) &=-\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\sum_{s=1}^S{ \log{P(y_s)} } \\ &\le-\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\sum_{s=1}^S{\Big( \mathbb{E}_{x\sim{P(\text{x}|y_s)}}\big[ \log{P(y_s|x;\theta_{x\rightarrow{y}})} \big]-\text{KL}\big(P(\text{x}|y_s)\|P(\text{x})\big) \Big)} \\ &\approx-\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\sum_{s=1}^S{\Big( \frac{1}{K}\sum_{k=1}^K{ \log{P(y_s|x_k;\theta_{x\rightarrow{y}})} }-\text{KL}\big(P(\text{x}|y_s)\|P(\text{x})\big) \Big)} \\ &=\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}}), \end{aligned} \\ \text{where }x_k\sim{P(\text{x}|y_s;\theta_{y\rightarrow{x}})}. \end{gathered}\]

위처럼 새롭게 정의된 $\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}})$ 을 미분하여 보면 KL-Divergence term은 없어질 것이고, 아래와 같이 파라미터는 업데이트 될 것입니다.

\[\begin{gathered} \theta_{x\rightarrow{y}}\leftarrow\theta_{x\rightarrow{y}}-\eta\nabla_{\theta_{x\rightarrow{y}}}\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}}), \\ \text{where } \nabla_{\theta_{x\rightarrow{y}}}\tilde{\mathcal{L}}(\theta_{x\rightarrow{y}})=-\nabla_{\theta_{x\rightarrow{y}}}\sum_{n=1}^N{ \log{P(y_n|x_n;\theta_{x\rightarrow{y}})} }-\nabla_{\theta_{x\rightarrow{y}}}\frac{1}{K}\sum_{s=1}^S{ \sum_{k=1}^K{ \log{P(y_s|x_k;\theta_{x\rightarrow{y}})} } }. \end{gathered}\]

이 수식을 해석해보면 흥미롭습니다. 두 번째 term은 반대쪽 모델 $\theta_{y\rightarrow{x}}$ 에서 $K$ 번 sampling한 $x_k$ 를 신경망의 입력으로 주었을 때, $y_s$ 에 대한 negative log likelihood를 최소화하도록 gradient를 계산하는 것을 볼 수 있습니다. 실제로 BT에서는 $K=1$ 일 때, sampling한 결과를 pseudo sentence로 삼아 신경망의 입력으로 넣어주고 있습니다. 그러므로 우리가 Back-Translation을 수행하는 것은 앞서 정의한 $\mathcal{L}(\theta_{x\rightarrow{y}})$ 를 최소화 하는 것과 같다라는 것을 알 수 있습니다.

Tagged Back-Translation을 수식으로 풀어보기

저는 사실 앞선 수식을 본 이후로 KL-Divergence term이 그렇게 사라지는 것이 영 아쉬웠습니다. 예를 들어, VAE에서는 KL-Divergencce term이 regularization term으로 매우 큰 역할을 수행하기도 하거니와, 어쨌든 KLD term이 최소화 된다면 $\log{P(y)}$ 가 좀 더 잘 최대화 될 것으로 보이기 때문입니다. 그러던차에 Noise added BT와 Tagged BT를 보고 위의 수식을 해당 방법들에 맞게 다시 전개 해보았습니다. 랜덤 변수 $c$ 를 도입해서 BT 여부를 알려주는 tag를 조건부 확률분포 함수 $\log{P(y|x,c)}$ 로 바꾸었습니다.

\[\begin{aligned} \log{P(y)} &=\log{\sum_{c\in\mathcal{C}}{ \sum_{x\in\mathcal{X}}{ P(x,y,c) } }} \\ &=\log{\sum_{c\in\mathcal{C}}{ \sum_{x\in\mathcal{X}}{ P(y|x,c)P(x|c)P(c) } }} \\ &=\log{\sum_{c\in\mathcal{C}}{ \sum_{x\in\mathcal{X}}{ \frac{P(y|x,c)P(x|c)}{P(x|y,c)}P(x|y,c)P(c) } }} \\ &\ge\sum_{c\in\mathcal{C}}{P(c) \sum_{x\in\mathcal{X}}{P(x|y,c) \log\frac{P(y|x,c)P(x|c)}{P(x|y,c)} } } \\ &=\mathbb{E}_{c\sim{P(\text{c})}}\bigg[ \mathbb{E}_{x\sim{P(\text{x}|y,c)}}\Big[ \log{P(y|x,c)} \Big] -\text{KL}\Big(P(\text{x}|y,c)\|P(\text{x}|c)\Big) \bigg] \end{aligned}\]

위의 수식에 따르면, 샘플링된 $c$ 에 따라 $x$ 를 실제 parallel corpus에서 활용하거나 파라미터 $\theta_{y\rightarrow{x}}$ 의 신경망에서 샘플링하여 타깃 파라미터 $\theta_{x\rightarrow{y}}$ 의 신경망에 tag $c$ 와 함께 넣어, log-likelihood인 $f(x,c;\theta_{x\rightarrow{y}})$ 를 구할 것 입니다. 즉, 여기서 $P(\text{x}|y,c=\text{BT})$ 는 이미 반대쪽 모델에 noise가 추가된 형태라고 보아야 할 것입니다.

이때 KLD term을 해석해본다면 재미있을 것 같습니다. 좌변을 최대화 하기 위해서는 KLD term이 최소화 되어야 할 것입니다. 따라서 분포 $P(\text{x}|y,c)$ 와 $P(\text{x}|c)$ 는 최대한 같아져야 할 것입니다. – 여기서 $c\ne\text{BT}$ 인 경우는 일단 제외하고 생각하도록 하겠습니다. 이에따라 랜덤변수 $\text{x}$ 와 $\text{y}$ 의 mutual information이 최소가 될 것입니다. 즉, 이것의 의미는 $y$ 의 정보에 상관 없이 pseudo corpus 자체의 언어모델 $P(\text{x}|c)$ 를 따르도록 될 것이란 것이고, 또한 이로 인해 $y\rightarrow{x}$ 의 번역 품질이 낮아질 것이라고 예상할 수 있습니다. 실제로 Noise added BT[7]의 경우에 일부러 noise를 섞어 번역의 품질을 희생시켰으며, 그 과정에서 bias를 학습하지 않도록 할 수 있었습니다.

사족: 샘플링 방식을 학습하는 것은 어떨까?

앞서 언급한대로 $x\sim{P(\text{x}|y,c)}$ 과정에서 이미 우리는 noise가 추가된 형태로 이해해볼 수 있을 것 같습니다. 즉, 기존의 $\theta_{y\rightarrow{x}}$ 함수를 한번 더 감싸서 noise added BT를 구현할 수도 있을 것입니다. 또한 KL term에서 $P(\text{x}|y,c)$ 는 $P(\text{x})$ 가 아닌 $P(\text{x}|c)$ 와 가까워지도록 하였기 때문에, 만약 우리가 noise를 섞어주는 방식도 parameterize(e.g. neural network)한다면 학습에 활용할 수 있을 것입니다.

정리하며

이번 포스팅에서는 monolingual corpus를 통해 NMT의 성능을 향상시키는 가장 대표적인 방법인 Back-Translation에 대해서 살펴보았습니다. BT는 간단한 방법과 이에 비해 높은 성능 향상을 인해 널리 사랑받고 있는 방법 중 하나입니다. 하지만 아쉽게도 low-resource NMT 상황이 아니면, original text보단 translationese를 번역하는데 대부분의 성능 향상이 집중되는 것을 확인할 수 있었습니다. 그렇다고 해서 BT가 별로다라는 이야기는 아닙니다. 어쨌든 low-resource NMT에서는 매우 강력한 힘을 발휘하고 있으며, high-resource(?) NMT에서도 어쨌든 득실을 따져보면 득이 더 크기 때문입니다.

또한 기존의 BT는 직관에 의해서 보통 설명이 되기 마련이었는데, [9]와 같은 방법을 통해 우리는 BT를 좀 더 수식적으로도 이해할 수 있었고, 한 발 더 나아가 Tagged BT에 대해서도 새롭게 수식으로 접근해보는 시간도 가져보았습니다. 위와 같이 수식을 통해 접근을 함으로써, 우리는 BT에 대한 더 나은 이해와 더 높은 성능 개선을 위한 한 걸음을 더 나아갈 수 있을 것이라고 생각합니다.

참고문헌

Search