Introduction to Deep Time-series Anomaly Detection

이번 포스팅에서는 시계열(time-series) 또는 시퀀셜(sequntial) 데이터에 대한 anomaly detection 기법을 이야기하고자 합니다. 사실 시계열 데이터는 데이터의 발생 시점(e.g. interval)도 중요한 feature인데 반해, 단순한 시퀀셜 데이터는 보통 순서 정보만 활용됩니다. 하지만 딥러닝의 대부분의 모델들은 기본적으로 시퀀셜 데이터만 다루도록 설계되어 있습니다. 이 포스팅은 딥러닝을 활용한 일반적인 방법론에 대해 이야기하고자 하므로, 시계열 데이터의 샘플간 time interval이 동일하다고 가정하고 seasonality와 같은 issue는 배제하고 이야기하고자 합니다. 즉, 비록 시계열 데이터이긴 하지만 일반적인 시퀀셜 데이터와 같이 다루도록 하겠습니다. 추후 다른 포스팅에서 interval 또는 seasonality와 같은 issue에 대해서 다루도록 하겠습니다. – 딥러닝을 활용한 이상탐지에 대한 앞선 포스팅[1, 2, 3]도 참고 바랍니다.

Previous Methods

사실 이상탐지의 대부분 application들은 의외로 시계열 데이터인 경우가 많습니다. Computer vision 분야에서의 image anomaly detection과 같은 case를 제외한다면, 특히 numeric data 또는 tabular data인 경우 대부분이 시계열 데이터로 구성되어 있는 경우가 많습니다. 따라서 예전부터 이상탐지 분야에서 시계열 데이터에 대한 이상탐지에 대한 연구가 많이 이루어져 왔습니다. 하지만 이에 반해, 현재 딥러닝에서의 이상탐지 연구들은 대부분 iid 기반이 많은 것이 사실입니다.

Univariate Time-series Anomaly Detection

보통 시계열 이상탐지 연구는 univariate time-series 데이터에 대해서 연구되어왔습니다. Image에서의 이상탐지라고 한다면, 주어진 이미지가 정상 범위에서 벗어날 경우 이것에 대해서 탐지하는 문제가 될 것입니다. 이에 반해 시계열 이상탐지 문제는 주어진 기간동안의 신호들이 정상 범위에서 벗어날 경우 이것에 대해서 탐지할 수 있어야 합니다. 예를 들어 심장 박동의 이상을 탐지하는 문제라고 한다면, 주어진 시간동안의 심장의 움직임에 대한 신호들을 가지고 해당 시간 내에 비정상적인 심장의 움직임이 있었는지 탐지하는 문제가 될 것입니다.

딥러닝 이전에는 DTW(Dynamic Time Warping)이나 ARIMA를 활용한 방법들도 많이 연구되었습니다. 딥러닝 모델을 활용해서도 여러가지 연구가 진행되었으나, 오늘의 주요 주제는 아니므로 넘어가도록 하겠습니다.

Multivariate Time-series Anomaly Detection

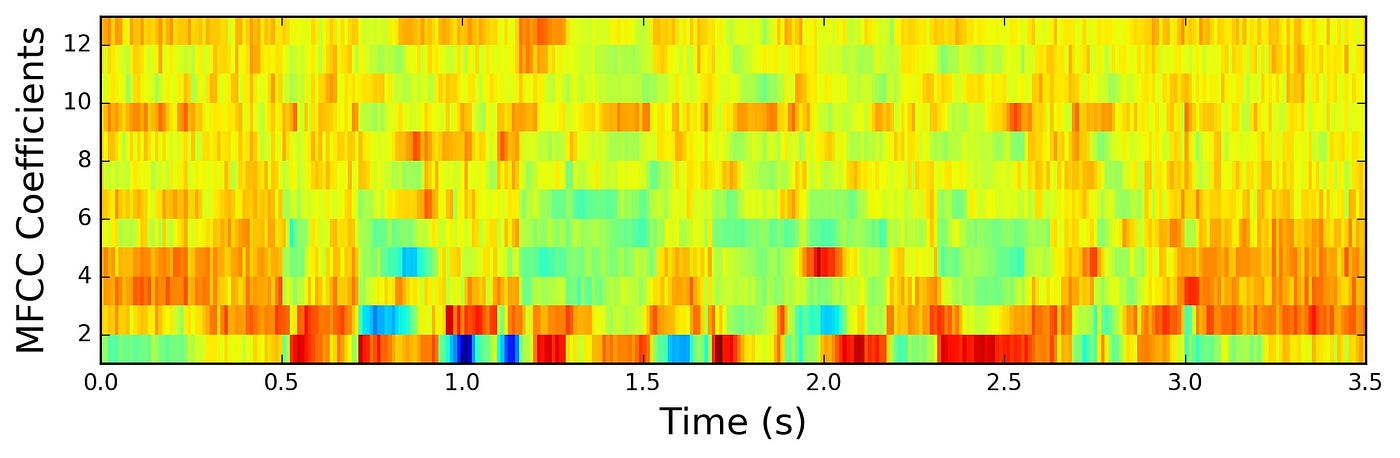
사실 오늘 주로 다루고자 하는 주제는 multivariate time-series 데이터에 대한 이상탐지입니다. 예를 들어, 위의 그림은 univariate time-series 데이터인 오디오 신호를 MFCC로 나타낸 것입니다. 위의 그림에서 x축은 시간을 나타내고, y축은 주파수 대역을 의미합니다. 따라서 특정 시간에 발생한 전체 주파수 대역에서의 신호의 세기가 multivariate vector로 나타내어질 수 있을 것입니다. 그럼 정해진 시간동안의 multivariate vector들의 시퀀스가 주어졌을 때, 해당 벡터들의 시퀀스가 정상 범위 내에 있는지 판단하는 문제가 될 것입니다.

사실 univariate time-series anomaly detection은 심장박동 이상탐지와 같은 문제에서는 훌륭하게 동작할 수 있지만, 많은 문제에 그대로 적용되기에는 어려움이 있습니다. 위의 오디오 신호에 대한 예제를 포함하여, 많은 반례를 생각해볼 수 있습니다. 예를 들어 제가 DEVIEW 2019에서 발표[4]할 때 데모로 소개해드렸던 로봇팔 이상탐지의 경우도 해당 될 수 있습니다.

해당 로봇팔은 6개의 축을 가지고 있습니다. 즉, 6개의 전기모터로 구성되어 있고, 이 모터에 들어가는 전류값(current)을 신호로 삼아서 이상탐지 문제를 접근해 볼 수 있을 것입니다. 이때, 각 축 별로 univariate time-series 이상탐지 모델을 만들어 적용해볼 수도 있을 것입니다. 하지만 이 경우에는 각 축간의 상호작용은 전혀 파악할 수 없을 것입니다. 예를 들어 1번 축이 높은 값일 때는 다른 축들이 낮은 값을 지녀야 한다던지와 같은 상황에 대해서는 대처할 수 없을 것입니다. 따라서 이러한 문제에서는 multivariate time-series 모델을 도입하여, 각 feature 사이의 상관관계까지도 학습할 수 있습니다.

이때, 기존의 shallow 기법들은 univariate 위에서의 time-series를 다루기에도 벅찬 상황이기 때문에, 딥러닝을 활용한 이상탐지 모델링 기법이 큰 힘을 발휘할 수 있습니다.

Deep Time-series Anomaly Detection

재미있게도 일찍이 딥러닝 이전의 시절에도 LSTM의 존재는 있었지만, 당시에는 데이터와 컴퓨팅 파워의 부족으로 인해서 부담스러운 존재였던 것도 사실입니다. 하지만 이제는 이전의 문제들이 대부분 해결되어 LSTM 따위는 아무런 부담없이 학습할 수 있게 되었습니다. 따라서 우리가 풀고자 하는 데이터가 시퀀셜 또는 시계열의 성격(샘플이 매번 독립적으로 같은 분포에서 샘플링 되는 것이 아니라면)을 갖고 있다면, RNN 계열의 모델을 활용해 보는 것도 매우 좋은 방법일 것 입니다.

Using IID Models with Flatten Vectors

하지만 바로 RNN과 같은 시퀀셜 모델을 도입하기에 앞서, time-series 데이터를 1차원의 tensor로 flatten하여 일반적인 iid 모델에 넣어보는 것도 좋은 시도(or baseline)가 될 수 있습니다.

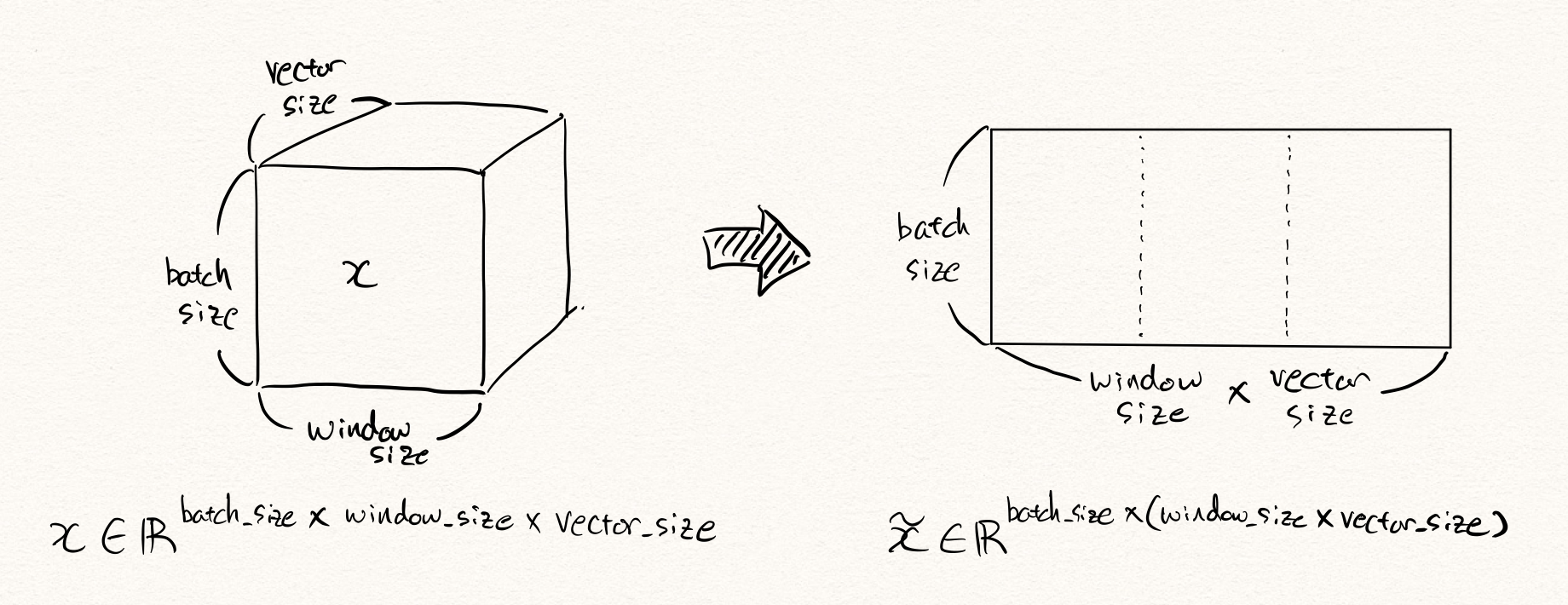
6차원 time-series 로봇팔 데이터를 예로 들어 보겠습니다. 만약 해당 데이터가 10Hz의 샘플링 주기를 가지고 있고, 우리는 약 5초간의 동작 데이터를 활용하여 이상을 탐지하고자 한다면, 한번의 이상탐지를 위해 주어진 데이터는 아래와 같은 형태를 따를 것입니다.

\[x\in\mathbb{R}^{10\times5\times6}\text{, where }x\sim{P_D(\text{x})}.\]

이때, 이것을 flatten한다면 $6\times10\times5=300$ 차원의 벡터 $\tilde{x}$ 가 될 것입니다. 그럼 이 300차원의 벡터를 오토인코더(autoencoder) $\mathcal{A}$ 에 넣어 학습 및 추론을 수행할 수 있을 것입니다. 이때 우리는 예전 포스팅에서 다루었던 대로 복원 오차(reconstruction error) 또는 RaPP[5]와 같은 방법들을 통해 이상 샘플을 탐지할 수 있습니다.

\[\begin{gathered} \text{AnomalyScore}(x)=||\tilde{x}-\mathcal{A}(\tilde{x})|| \\ \text{or} \\ \text{RaPP}(x)=\sum_{i=0}^{\ell}{||g_{:i}(\tilde{x})-g_{:i}\circ\mathcal{A}(\tilde{x})||}\text{, where }\mathcal{A}=f_{:\ell}\circ{g_{:\ell}}. \end{gathered}\]

하지만 이러한 경우(특히 fully-connected layer와 같은 레이어들로 구성되어 있는)에는, 시계열의 특성을 활용한다기보단 모든 feature들과의 상관관계를 모두 따져보는 것이기 떄문에, 필요 이상으로 배워야 하는 정보들이 많아지고 이에 따라 모델 웨이트 파라미터들도 훨씬 많아져서 모델이 학습하는데 불리하게 작용할 수 밖에 없습니다.

Single RNN based Methods

그럼 이제 본격적으로 RNN 계열 모델들을 활용하는 방법을 이야기 해보겠습니다. 가장 간단한 방법으로는 하나의 RNN을 활용한 generative modeling을 생각해볼 수 있습니다. 이를 위해서는 아래와 같이 RNN $f$ 가 $x_{<t}$ 를 입력 받아, $x_t$ 를 예측하는 형태가 될 것입니다.

\[\hat{\theta}=\text{argmax}\sum_{t=1}^{T}{\log{P(x_t|x_{<t};\theta)}}\text{, where }x_{1:T}=\{x_1,\cdots,x_T\}.\]

그럼 이때 likelihood는 아래와 같이 계산될 수 있습니다.

\[\log{P(x_t|x_{<t};\theta)}=\|x_t-f_\theta(x_{<t})\|\]

이때 그럼 우리는 이 likelihood를 anomaly score로 삼아 이상탐지를 수행할 수 있을 것입니다. – 기존 오토인코더 방식에서는 reconstruction error가 likelihood가 됩니다.

\[\text{AnomalyScore}(x_{1:T})=\sum_{t=1}^T{\|x_t-f_\theta(x_{<t})\|}\]

즉, RNN은 다음 time-step의 값을 예측하는 task를 통해 자연스럽게 정상 분포를 학습하게 되고, 비정상 샘플이 주어진다면 likelihood의 값이 낮게 나오게 될 것이므로 우리는 이를 활용하여 시계열 이상탐지를 수행할 수 있는 것입니다.

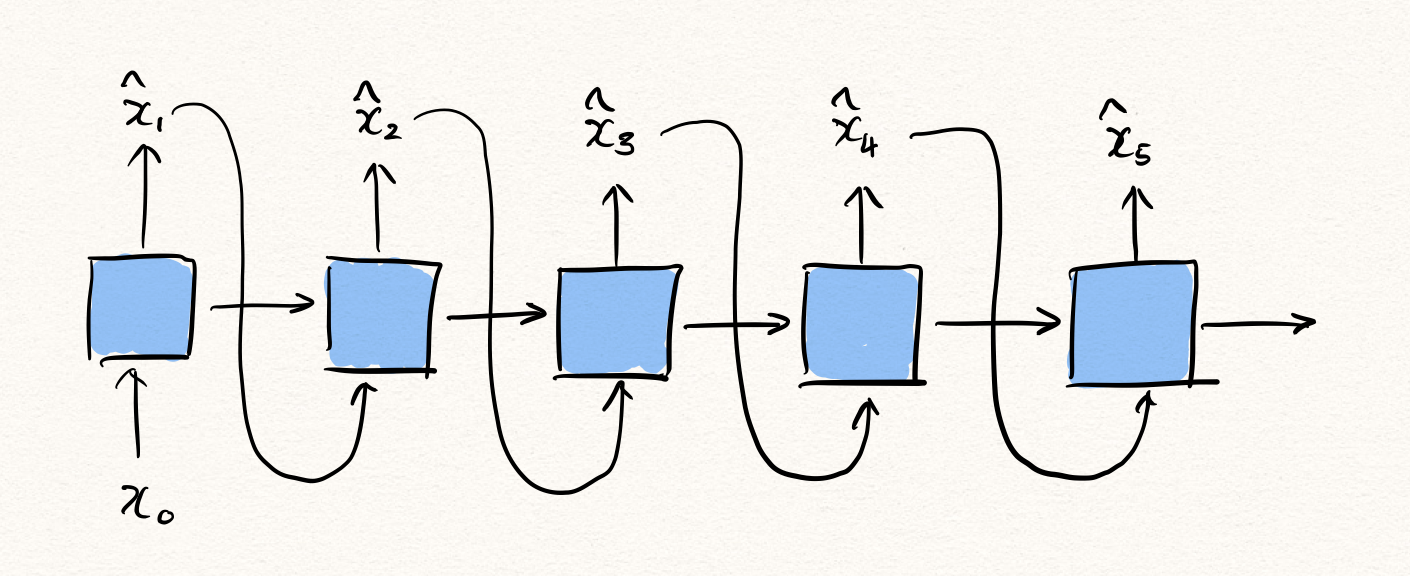
하지만 아쉽게도 이 모델은 auto-regressive(자기회귀) 특성을 가지므로 한계가 있습니다. 한 방향으로만 추론이 이루어지기 때문에, $x_t$ 에 대해서 추론을 수행하고자 할 때, $t$ 이전 시점의 데이터들로부터만 정보를 얻어올 수 있습니다. 하지만 $t$ 이후 시점으로부터도 정보를 얻어와 $x_t$ 를 추론할 수 있다면 훨씬 더 정확한 예측을 수행할 수 있을 것입니다.

이것은 이상탐지 문제는 generation에 집중하는 task가 아니기 때문이라고 해석해 볼 수 있습니다. 예를 들어 기계 번역(machine translation)과 같은 언어 모델링(language modeling) task에서는 신경망이 입력과 다른 새로운 문장을 출력해 내야 하는 것이지만, 이상탐지 task에서는 주어진 샘플을 얼마나 잘 똑같이 복원해 내는지가 관건이기 때문이라고 볼 수 있습니다. 즉, 다시말하면 기존의 NLG task에서는 입력과 출력이 다른 형태이지만, 이상탐지 task에서는 입출력이 같은 형태이기 때문에 다른 접근법이 가능하다는 것입니다.

Encoder-Decoder based Methods

그럼 한 발 더 나아가 sequence to sequence와 같은 encoder + decoder 기반의 아키텍처를 생각해볼 수 있습니다.

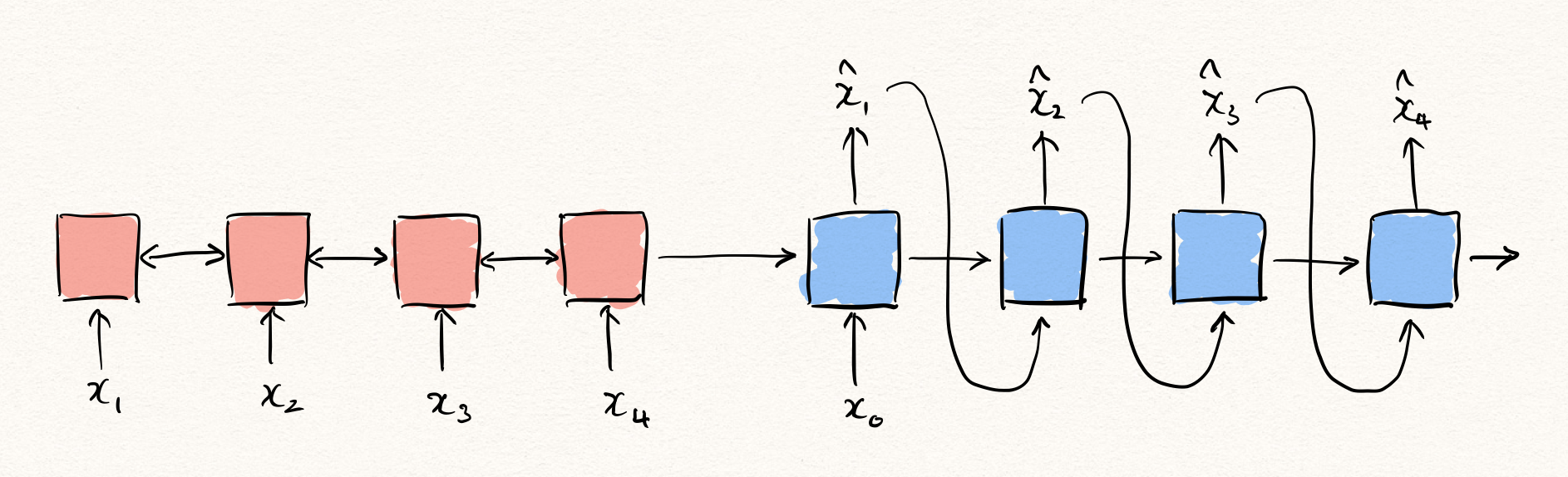
다만, 이 아키텍처는 주어진 입력을 그대로 복원해내야 하기 때문에, 기존의 sequence to sequence와 차별하기 위해서 sequence autoencoder(SeqAE)라고 부르도록 하겠습니다. 이 SeqAE는 여전히 auto-regressive한 decoder를 갖고 있지만, 어쨌든 encoder에서 주어진 모든 time-step을 볼 수 있었기 때문에, 앞서 설명한 아키텍처보다는 조금 더 유리한 부분을 가질 수 있습니다.

\[\hat{\theta}=\text{argmax}\sum_{t=1}^T{\log{P(x_t|x_{<t},z;\phi)}}\text{, where }z=g(x_{1:T};\psi)\text{ and }\theta=\{\phi,\psi\}.\]

이때 encoder $g$ 로부터 얻은 latent representation $z$ 는 오토인코더 관점에서 보면 bottleneck에서의 variable이라고 생각해 볼 수 있습니다. 즉, 우리는 encoder를 통해 $x_{1:T}$ 를 압축하여, decoder를 통해 순차적으로 풀어내는 것이라 볼 수 있습니다.

Attention?

이때 흔히 성능을 개선하기 위한 포인트로 attention을 추가하는 것을 고려해볼 수 있습니다. 예를 들어 기계번역을 위한 sequence to sequence(seq2seq) 아키텍처에서 attention이 추가 되면, seq2seq 내부 RNN의 hidden state의 capacity 부족 등의 문제로 인한 성능 하락을 막을 수 있습니다. 따라서 attention은 자연어처리 분야에서 매우 중대한 발전이라고 볼 수 있습니다.

하지만 이상탐지 문제 해결 관점에서는 attention을 곧바로 적용하기에는 무리가 있습니다. 기계번역과 같은 task에서는 더 나은 문장을 생성하기 위해서 RNN의 hidden state를 극복하기 위한 대안으로 제시되었지만, 이상탐지에서는 bottleneck의 latent representation $z$ (hidden state)에 압축된 정보가 무엇인지가 중요합니다. 비정상 샘플이었다면 정상적으로 압축이 수행되지 않아, $z$ 에 복원을 위한 충분한 정보가 담겨있지 않을 것이기 때문입니다. 하지만 여기서 우리가 attention을 사용한다면, $z$ 의 압축 품질 여부와 상관 없이 decoder는 attention을 통해 encoder에서 충분한 정보를 access할 수 있을 것이기 때문입니다. 따라서 attention을 시도해 보는 것은 좋지만, 이 문제를 해결하는 방향이 함께 시도[6]되어야 할 것이라 생각합니다.

Teacher Forcing

사실 앞서 RNN을 통해 이상탐지를 수행하는 방법에 대해서 설명할 때, 빼 놓은 부분이 있습니다. 바로 학습 및 추론 방법 입니다. 먼저, 추론 상황을 가정해보겠습니다. 자연어생성(NLG)과 같은 Auto-regressive한 task를 수행하는 경우, 보통은 decoder를 통해 출력을 뱉어낼 때 decoder의 입력은 이전 time-step의 decoder의 출력이 됩니다.

\[\hat{x}_t=\text{argmax}\log{P(\text{x}_t|\hat{x}_{<t};\theta)}\]

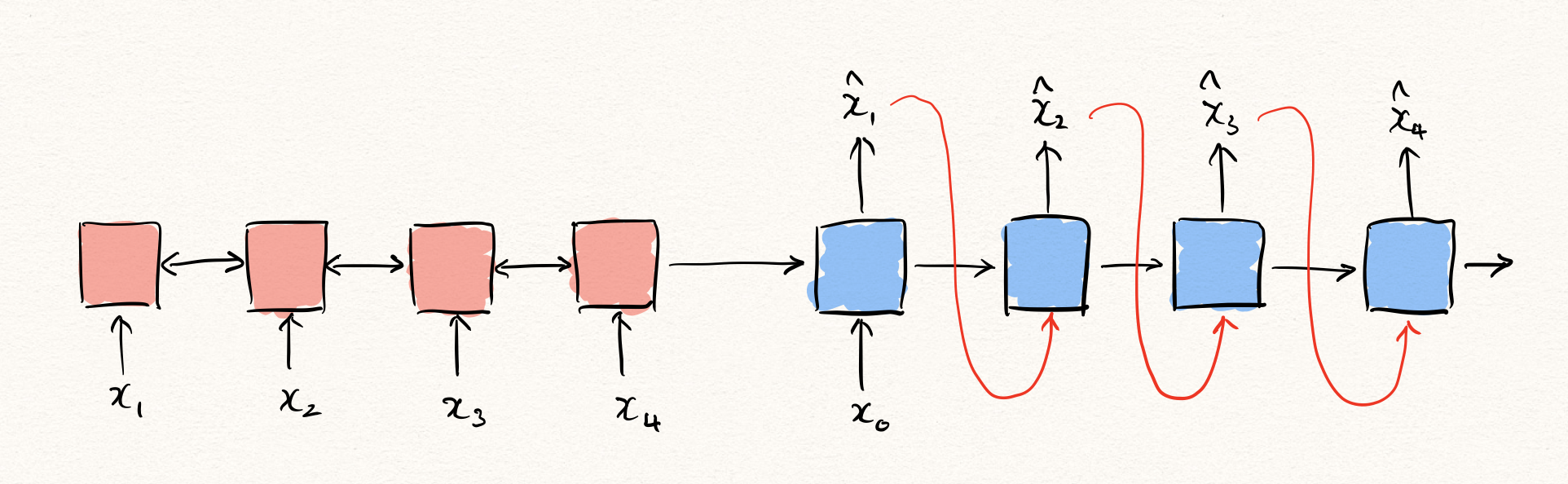
하지만 문제는 학습을 수행할 때는 이와 같은 방법으로 진행하는 것은 문제가 될 수 있습니다. 우리는 likelihood를 maximize 하기 때문에, 원래의 정답 $x_t$ 와 decoder $f$ 의 출력 $\hat{x}_t$ 의 차이를 구합니다. 이것은 수식으로 나타내면 아래와 같습니다.

\[\begin{aligned} \mathcal{L}(\theta)&=-\sum_{t=1}^T{\log{P(x_t|x_{<t};\theta)}} \\ &=-\|x_1-f_\theta(x_0)\|_2^2-\|x_2-f_\theta(x_{0:1})\|_2^2-\cdots-\|x_T-f_\theta(x_{0:T-1})\|_2^2 \end{aligned}\]

즉, decoder의 입력으로 $\hat{x}{<t}$ 가 아닌, $x{<t}$ 가 주어졌기 때문에, 가능한 것입니다. 만약 학습할 때에 $\hat{x}_{<t}$ 가 주어진 상태에서 decoder의 출력값과 $x_t$ 와의 MSE를 구한다면, 우리는 Maximum Likelihood Estimation (MLE)를 한다고 할 수 없는 것입니다. 따라서 딥러닝에서 MLE를 통해 시퀀셜 데이터를 학습할 때에는 teacher forcing이라는 방법을 통해 학습을 수행하는 것이 보통입니다.

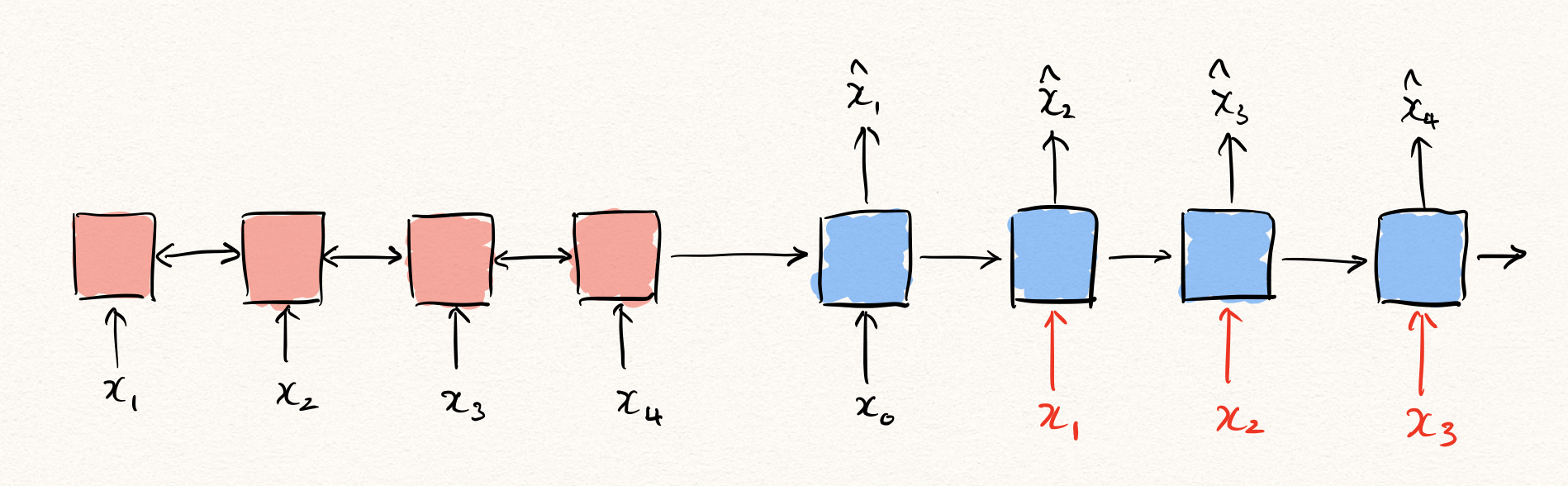
Teacher forcing은 위 그림과 같이 학습 과정에서 decoder의 이전 time-step의 출력이 아닌 이전 time-step의 실제 정답을 decoder에 입력으로 넣어주는 것입니다. 우리는 이런 teacher forcing을 통해 auto-regressive task에서 RNN을 MLE를 통해 학습할 수 있게 됩니다.

문제는 여기에서 발생하게 됩니다.

How to Inference: Likelihood vs Generation

문제를 디테일하게 이야기하기에 앞서, SeqAE에서의 이상탐지를 위한 추론 방법에 대해서 좀 더 이야기하려 합니다. 앞서는 단순히 NLG task와 같은 추론 방법인 generation에 대해서 이야기 했는데, 사실 iid 데이터의 오토인코더를 활용한 reconstruction error 기반의 이상탐지 방법은 분포가 gaussian이라는 가정 하에 likelihood를 구하는 것이라고 볼 수 있습니다.

따라서, SeqAE에서도 generation이 아닌, likelihood를 통해 reconstruction error를 구하고, 그것을 통해 이상탐지 추론을 수행해야 하는 것은 아닌가 하는 합리적인 의심이 생길 수 있습니다. 그럼 위에서 적은데로 teacher forcing 방법을 추론에서 수행할 수도 있다는 이야기겠죠. 특히, NLG와 달리 이상탐지 task에서는 입력을 그대로 복원해내기 때문에, SeqAE가 출력해야 하는 값을 알고 있다는 점에서 teacher forcing이 가능합니다. – 이와 반대로 기계번역과 같은 NLG task에서는 test과정에서는 seq2seq의 출력값을 모르기 때문에 generation을 수행할 수 밖에 없습니다.

그런데 문제는 teacher forcing을 통해 reconstruction을 구하게 된다면 너무나도 쉬운 task가 되어버린다는 것입니다. 예를 들어 아래와 같이 MNIST를 시퀀셜 데이터로 취급해서 이상탐지를 똑같이 수행해볼 수 있을겁니다. 즉, $28\times28$ 의 MNIST 이미지를 28차원의 벡터가 28 time-step 존재하는 시퀀셜 데이터로 생각해볼 수 있을 것입니다.

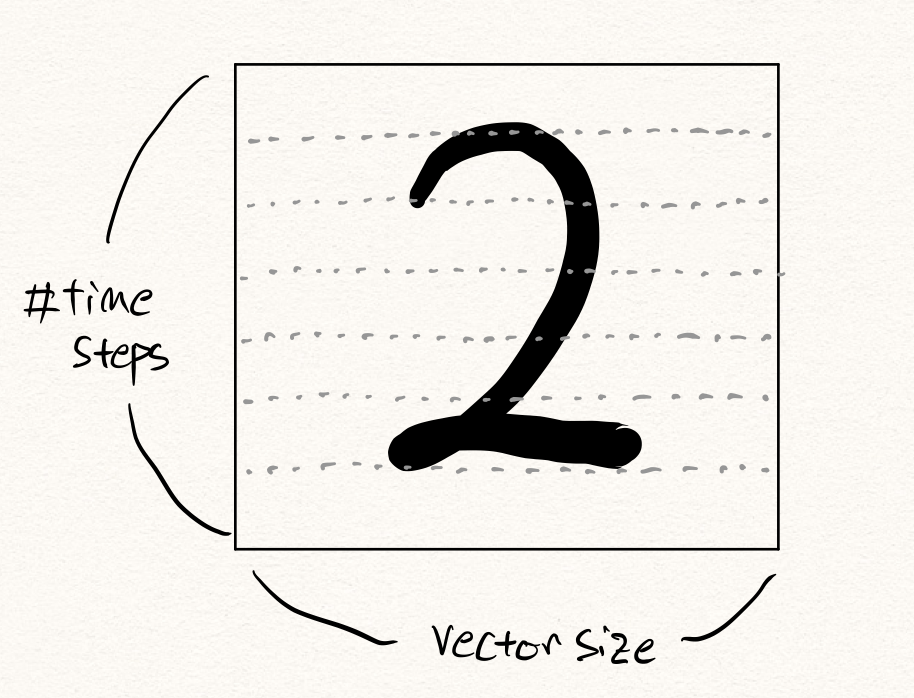
그럼 teacher forcing을 추론에서 수행하게 된다면, decoder는 이전 time-step에서 틀린 출력 $\hat{x}{t-1}$ 을 뱉어냈더라도, 현재 time-step의 입력으로 정답 $x{t-1}$ 을 받게 될겁니다. 그럼 현재 time-step의 출력 $\hat{x}t$ 를 예측하는 것은 너무나도 쉬워지게 됩니다. 당장 MNIST의 경우에만 보더라도 $x{t-1}$ 과 거의 유사한 픽셀값을 뱉어내면 거의 맞출테니까요. 즉, 학습 때 보지 못한 형태의 이미지가 들어오더라도 같은 방법을 통해서 대충 맞출 수 있게 되는 것입니다.

그러므로 우리는 SeqAE와 같은 모델에서는 teacher forcing을 통해 likelihood를 구하는 것이 아닌, generation 방식으로 통해 이상탐지의 추론을 수행해야 함을 확인할 수 있습니다. 즉, 원래 평소(NLG task등에서 하던 방법)에 하던대로 하면 됩니다.

Begining of Posterior Collapse

그런데 문제는 또 남아있습니다. teacher forcing을 통해 학습을 진행할 때에도 마찬가지 상황이 발생한다는 것입니다. 특히나 NLG와 같은 discrete value를 출력하는 task가 아니라 continuous value를 뱉어내는 task이기 때문에, $x_{t-1}$ 와 $x_t$ 의 차이가 적어서 생기는 문제로도 생각해볼 수 있습니다. 따라서 teacher forcing을 통해 학습을 수행할 때에도, 너무나도 쉬운 나머지 encoder로부터 많은 정보를 받을 필요가 없어지게 됩니다. 예를 들어 아래와 같이 2 또는 3에 대해서 학습할 때, 한번의 도움만 있으면 충분하지 않을까요?

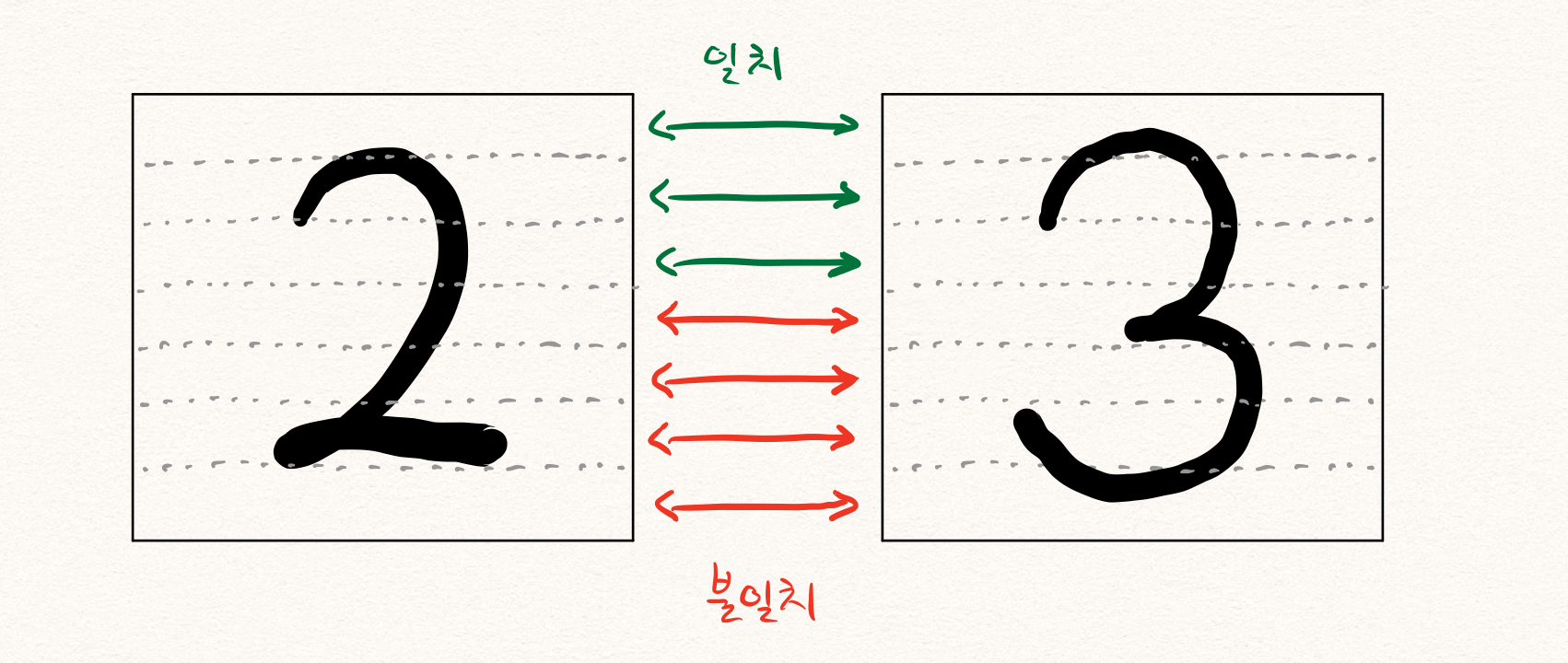
그럼 encoder는 주어진 샘플에 대해서 많은 정보를 인코딩하지 않도록 학습될겁니다. 이것은 결국 추론 단계에서 비정상 샘플이 주어졌을 때, 안좋은 영향을 끼치게 될 것입니다. 이렇게 encoder가 어떤 샘플이 주어지든 비슷한 latent representation으로 인코딩하게 되는 현상을 posterior collapse라고 부릅니다. 물론 위의 예제에서처럼 어쨌든 2와 3을 구분하기 위한 정보가 어느정도는 담겨있을 것이기 때문에, 아무런 정보가 없지는 않겠지만 posterior collapse의 경향이 나타난다고 볼 수 있습니다.

Needs of Sequence Variational Autoencoder (SeqVAE)

우리는 앞선 포스팅에서 VAE가 Variational Information Bottleneck(VIB)를 가지고 있어서 이상탐지 task에서 더 뛰어난 성능을 보인다고 이야기 한 바 있습니다. 그럼 마찬가지로 SeqAE에서도 한발 더 나아가 SeqVAE를 생각해 볼 수 있을 것입니다. 문제는 이 SeqVAE가 posterior collapse에 매우 취약하다는 것입니다.

\[\mathcal{L}(\phi,\psi)=-\mathbb{E}_{z\sim{q(\text{z}|x;\psi)}}\Big[\log{p(x|z;\phi)}\Big]+\text{KL}\Big(q(z|x;\psi)\|p(z)\Big)\]

위와 같이 VAE 또는 SeqVAE는 첫 번째 reconstruction term과 함께 두 번째 KL-divergence term도 최소화해야 합니다. 문제는 SeqVAE는 앞서 언급한 문제 때문에 디코더는 아주 적은 정보만 있어도 디코딩을 잘 할 수 있습니다. 더욱이 KLD term이 있기 때문에 인코더는 더더욱 아무 일을 하지 않으려 노력하게 됩니다. – 아마 인코더는 어떤 샘플이 들어오더라도 $\mu=0$ , $\sigma=1$ 을 뱉어내고 싶을 겁니다. 즉, SeqVAE는 앞서 언급한 posterior collapse 문제를 더욱 심하게 겪게 됩니다.

그럼 이런 posterior collapse가 심하게 존재하고 있는 상황에서는 인코더에 어떤 샘플이 주어지더라도 인코더의 출력값 latent representation $z$ 는 변화가 없을(KLD term이 0이 될) 것이기 때문에, 디코더는 generation형식으로 inference를 수행하게 되면 어떤 샘플이 들어오든 항상 같은 출력값을 뱉어내게 됩니다. 마치 Generative Adversarial Networks (GAN)에서의 mode collapse와 비슷한 현상이 결과로 나타나는 것이지요. – 이러한 현상이 나타나는 원인은 다릅니다.

따라서 이러한 VAE의 posterior collapse를 해결하기 위한 연구들[7, 8, 9, 10, 11]도 많이 이루어져 왔습니다. 하지만 대부분은 text domain에서의 문제 셋팅(discrete value + variable length)에 집중하고 있고, continuous data에 대한 이상탐지 문제에서의 posterior collapse 현상에 대한 해결책을 제시하는 연구는 아직 많지 않은 것이 사실입니다. 다행히도 기존의 연구들이 집중하고 있는 문제 셋팅이 이상탐지에 비해서 좀 더 어려운 문제 셋팅이다보니, 기존의 연구들로부터 많은 도움은 받을 수 있겠지만 본격적인 연구가 이루어지지 않았다는 것이죠. 따라서 sequential modeling을 활용한 이상탐지 문제 해결을 위한 연구들이 본격적으로 많이 이루어져야 함을 알 수 있습니다.

Conclusion

이번 포스팅에서는 딥러닝 모델을 활용한 시계열(또는 시퀀셜) 데이터에 대한 이상탐지 방법과 어떤 어려움들이 있는지 살펴보았습니다. 사실 단순히 RNN이나 seq2seq와 같은 아키텍처를 쓰면 모든 문제가 해결될 것 같지만, 이 포스팅에서 살펴본 것처럼 고려해야 할 점들이 많이 남아 있고, 아직 풀어야 할 문제들도 남아있는 것이 사실입니다. 다음 포스팅에서는 앞서 언급한 문제들을 마키나락스에서 해결한 사례를 공유하고자 합니다.

References

• [1] Ki Hyun Kim, RaPP - Novelty Detection with Reconstruction along Projection Pathway, blog, 2020
• [2] Ki Hyun Kim, Autoencoder based Anomaly Detection, blog, 2020
• [3] Ki Hyun Kim, Introduction to Deep Anomaly Detection, blog, 2020
• [4] Ki Hyun Kim, Operational AI: Building a Lifelong Learning Anomaly Detection System, DEVIEW, 2019
• [5] Ki Hyun Kim et al., Rapp: Novelty Detection with Reconstruction along Projection Pathway, ICLR, 2020
• [6] Bahuleyan et al., Variational Attention for Sequence-to-Sequence Models, ICCL, 2018
• [7] Cremer et al., Inference Suboptimality in Variational Autoencoders, ICML, 2018
• [8] Yoon Kim et al., Semi-Amortized Variational Autoencoders, ICML, 2018
• [9] Yan et al., Re-balancing Variational Autoencoder Loss for Molecule Sequence Generation, ArXiv, 2019
• [10] Zhao et al., InfoVAE: Balancing Learning and Inference in Variational Autoencoders, AAAI, 2019
• [11] He et al., LAGGING INFERENCE NETWORKS AND POSTERIOR COLLAPSE IN VARIATIONAL AUTOENCODERS, ICLR, 2019
• [12] Kieu et al., Outlier Detection for Time Series with Recurrent Autoencoder Ensembles, IJCAI, 2019
• [13] Malhotra et al., LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection, ICML Workshop, 2016
• [14] pavithrasv, Timeseries anomaly detection using an Autoencoder, Keras Tutorial, 2020
• [15] Park, Jinman, RNN based Time-series Anomaly Detector Model Implemented in Pytorch, GitHub, 2018